Задания к контрольной работе №9. В партии из Nизделий имеют скрытый дефект nизделий (табл.1)

Задание №1

В партии из Nизделий имеют скрытый дефект n изделий (табл.1). Какова вероятность того, что из взятых наугад m изделий k изделий являются дефектными?

Таблица 1

Задание №2

Три стрелка произвели залп по цели. Вероятность поражения цели первым стрелком равна ; для второго и третьего стрелков эти вероятности соответственно равны и 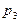. Найти вероятность того, что: a) только один из стрелков поразит цель; б) только два стрелка поразят цель; в) все три стрелка поразят цель.

; ; (а – последняя цифра зачетной книжки, b – предпоследняя цифра зачетной книжки).

Задание №3

На сборочное предприятие поступили однотипные комплектующие с тех заводов в количестве: с первого завода, со второго, с третьего (табл. 3). Вероятность качественного изготовления изделий на первом заводе , на втором , на третьем 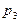. Какова вероятность того, что взятое случайным образом изделие будет качественным?

Таблица 3

Вариант							Вариант
		0,9		0,8		0,7			0,9		0,8		0,7
		0,8				0,7			0,8		0,7		0,9
		0,9		0,7		0,9			0,9		0,8		0,8
		0,7		0,9		0,8			0,8		0,6		0,7
		0,9		0,8		0,6			0,9		0,8		0,7
		0,8		0,8		0,9			0,9		0,7		0,8
		0,8		0,9		0,8			0,9		0,8		0,9
		0,7		0,8		0,9			0,9		0,7		0,7
		0,9		0,8		0,9			0,8		0,9		0,8
		0,8		0,7		0,8			0,8		0,8		0,9
		0,9		0,9		0,8			0,9		0,8		0,6
		0,8		0,9		0,8			0,8		0,7		0,8
		0,8		0,9		0,7			0,8		0,9		0,8
		0,9		0,7		0,7			0,9		0,8		0,9
		0,8		0,9		0,9			0,7		0,9		0,7

Задание №4

1) Контрольная работа состоит из шести задач. Вероятность выполнения студентом каждой задачи равна 0,4. Какова вероятность, что студент не выполнил: а) одну задачу; б) хотя бы две задачи; в) ни одной задачи?

2) Какова вероятность выпадения двойки при семи подбрасываниях правильной игральной кости: а) два раза; б) от двух до четырех раз; в) хотя бы два раза?

3) Какова вероятность появления решки при пяти подбрасываниях правильной монеты: а) один раз; б) хотя бы один раз; в) три раза?

4) Для данного участника игры вероятность набросить кольцо на колышек составляет 0,6. Найти вероятность набросить кольцо на колышек: а) один раз при трех бросках; б) хотя бы один раз при трех бросках; в) при шести бросках?

5) На самолете имеются шесть одинаковых двигателей. Вероятность нормальной работы каждого двигателя в полете равна 0,8. Какова вероятность того, что в полете возникнут неполадки: а) в одном полете; б) хотя бы в одном двигателе; в) в пяти двигателях?

6) Испытываются семь независимо работающих одинаковых прибора. Вероятность отказа каждого прибора при испытании равна 0,4. Какова вероятность того, что при испытании не откажут: а) два прибора; б) хотя бы два прибора; в) не более чем один прибор?

7) Вероятность того, что на некотором предприятии расход электроэнергии не превысит суточную норму, равна 0,6. Какова вероятность того, что расход электроэнергии превысит суточную норму: а) хотя бы три рабочих дня из проверенны 5; б) три дня из проверенных 4; в) не менее 2 дней из проверенных трех?

8) Вероятность того, что стрелок попадает в цель при одном выстреле равна 0,7. Производится шесть независимых выстрелов. Какова вероятность того, что пробоин в мишени окажется: а) шесть; б) хотя бы одна; в) более 2?

9) В горном районе создано семь автоматических сейсмических станций. Каждая станция в течении года может выйти из строя с вероятностью 0,3. Какова вероятность того, что в одном рассматриваемом году не выйдут из строя: а) хотя бы одна станция; б) хотя бы две станции; в) две станции?

10) Контрольная работа состоит из пяти вопросов. На каждый вопрос приведено пять ответов, один из которых правильный. Студент отвечает на вопросы наугад. Какова вероятность того, что правильных ответов будет: а) три; б) более двух; в) хотя бы один?

11) Вероятность того, что стрелок попадает в цель при каждом выстреле равна 0,7. Производится два независимых выстрела. Какова вероятность того, что стрелок попадает в цель: а) один раз; б) два раза; в) хотя бы один раз?

12) В горном районе создано три автоматических сейсмических станций. Каждая станция в течении года может выйти из строя с вероятностей 0,2. Какова вероятность того, что в одном рассматриваемом году не выйдут из строя: а) хотя бы одна станция; б) хотя бы две станции; в) две станции?

13) Контрольная работа состоит из четырех вопросов. На каждый вопрос приведено пять ответов, один из которых правильный. Студент отвечает на вопросы наугад. Какова вероятность того, что правильных ответов будет: а) два; б) менее двух; в) не более двух?

14) При высаживании непикированной рассады помидоров только 80% растений приживаются. Посажено два куста помидоров. Какова вероятность того, что приживется: а) один куст; б) хотя бы один куст; в) не более одного куста?

15) Какова вероятность того, что при трёх подбрасываниях правильной монеты герб выпадет: а) хотя бы два раза; б) два раза; в) ни одного раза?

16) Для данного участника игры вероятность набросить кольцо на колышек равна 0,35 (броски считать независимыми). Какова вероятность попадания: а) 75 раз при 200 попытках; б) более 70 раз при 200 попытках?

17) Аппаратура содержит 400 одинаково надежных независимо работающих элементов, вероятность отказа в течение года для каждого из которых равна 0,002. Какова вероятность того, что в течение рассматриваемого года в аппаратуре откажет: а) хотя бы один элемент; б) 4 элемент; в) 2 или 3 элемента?

18) Для данного баскетболиста вероятность забросить мяч в корзину при каждом броске равна 0,65. Произведено 50 бросков. Найти вероятность того, что попаданий окажется а) 35; б) не менее 25 и не более 40.

19) Вероятность попадания в цель при каждом выстреле равна 0,97. Произведено 100 независимых выстрелов. Какова вероятность, что окажется: а) 2 промаха; б) 2 или 4 промаха; в) более трёх промахов?

20) В круг радиуса R вписан квадрат. В круг случайным образом бросается 150 точек. Найти вероятность того, что попало в квадрат: а) 90 точек; б) более 95 точек.

21) Среднее число ошибочных соединений, приходящихся на одного телефонного абонента в течение года, равно 10. Какова вероятность того, что ошибочных соединений, приходящихся на одного абонента в течение полугода, окажется: а) три; б) пять; в) хотя бы одно?

22) А отрезок АВ длины 1 наудачу брошено 100 точек. Найти вероятность того, что: а) 20 точек; б) более 20 точек будут находится от точки А на расстоянии, меньшем 0,25. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

23) Упаковщик укладывает 900 деталей, проверенных ОТК или изготовленных рабочими, имеющими личное клеймо. Вероятность того, что деталь помечена личным клеймом, равна 0,005. Какова вероятность того, что деталей, помеченных личным клеймом, окажется: а) хотя бы две; б) 2; в) не менее 2?

24) За один цикл автомат изготавливает 500 деталей. Вероятность то, что деталь окажется бракованной, равна 0,02. Найти вероятность того, что за один цикл автомат изготовит: а) 12 бракованных деталей; б) более 10 бракованных деталей.

25) Некто приобрел 200 билетов лотереи. Известно, что вероятность выигрыша на один билет лотереи равна 0,002. Какова вероятность того, что среди приобретенных выигрышных билетов окажется: а) хотя бы пять; б) пять; в) от 1 до 3 включительно?

26) Вероятность появления успеха в каждом из 625 независимых испытаний равна 0,8. Найти вероятность того, что успех появится: а) 505 раз; б) не менее 475 раз.

27) Электростанция обслуживает сеть, в которой 700 лампочек, вероятность включения каждой из которых за время t равна 0,01. Какова вероятность того, что за время t включится: а) 3 лампочки; б) не более 2 лампочек; в) хотя бы две лампочки?

28) Какова вероятность того, что в столбике из наугад отобранных правильных монет число монет, расположенных гербом вверх будет: а) 50; б) от 45 до 55.

29) Испытываются 400 деталей, а вероятность того, что деталь выдержит испытание, равна 0,992. Какова вероятность того, что не выдержат испытания: а) 2 детали; б) более 3 деталей; в) от 2 до 5 включительно?

30) Отрезок разделен на четыре равные части. На отрезок наудачу брошено 20 точек. Определить вероятность того, что 5 точек попали на одну из четырех частей отрезка. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.

Задание №5

Задан закон распределения д. с. в. Х таблицей. Найти . Построить многоугольник распределения. Определить математическое ожидание 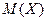, дисперсию , функцию распределения 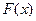и построить её график.

1.

	-6	-2
	0,1	0,3	0,2	0,3

2.

	-10	-6	-4
	0,2	0,5	0,1	0,1

3.

	-7	-6	-3
	0,3	0,1	0,2	0,1

4.

	-1
	0,5	0,1	0,1	0,2

5.

	-9	-7	-6
	0,4	0,1	0,1	0,3

6.

	-9
	0,6	0,1	0,1	0,1

7.

	-9	-8	-2	-1
	0,2	0,1	0,3	0,1

8.

	-3
	0,2	0,4	0,2	0,1

9.

	-8	-6	-3	-1
	0,1	0,1	0,1	0,5

10.

	-7
	0,1	0,2	0,4	0,1

11.

	-7
	0,15	0,2	0,35	0,1

12.

	-8
	0,4	0,15	0,2	0,2

13.

	-10	-7
	0,25	0,3	0,05	0,1

14.

	-7	-4
	0,45	0,1	0,2	0,05

15.

	-5
	0,15	0,35	0,2	0,2

16.

	-8	-6	-4
	0,2	0,2	0,1	0,25

17.

	-10
	0,05	0,3	0,1	0,15

18.

	-6	-4
	0,6	0,1	0,1	0,05

19.

	-10	-4
	0,4	0,05	0,1	0,2

20.

	-7	-5	-2
	0,35	0,2	0,1	0,3

21.

	-10	-6	-4
	0,2	0,15	0,4	0,05

22.

	-9	-6	-5	-3
	0,1	0,25	0,3	0,1

23.

	-4
	0,35	0,05	0,1	0,2

24.

	-8	-5	-1
	0,05	0,15	0,3	0,15

25.

	-1
	0,3	0,3	0,05	0,1

26.

	-9	-7	-5	-2
	0,15	0,45	0,1	0,25

27.

	-5
	0,1	0,5	0,05	0,05

28.

	-8	-2
	0,45	0,1	0,1	0,15

29.

	-2
	0,2	0,25	0,15	0,2

30.

	-10	-7	-3
	0,1	0,1	0,25	0,3

Задание №6

Задана плотность распределения вероятностей непрерывной случайной величины X. Найти параметр С, функцию распределения , математическое ожидание , дисперсию и вероятность попадания случайной величины X в интервал .

1.

2.

3.

4.

5.

6.

7.

8.

9.

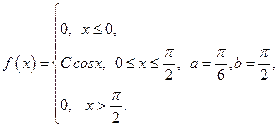
10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

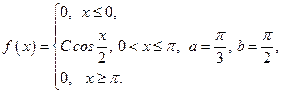
27.

28.

29.

30.

Не нашли, что искали? Воспользуйтесь поиском: