Образец выполнения задания 4.

Задача. Известно, что в русском языке имеется связь между количеством букв в слове и числом гласных букв в нем. Необходимо по данному отрывку из изречения известного ученого оценить указанную связь. Для этого необходимо составить двумерную случайную (Х,У), где Х – число букв в слове, У – число гласных букв в слове, и для нее вычислить выборочный коэффициент корреляции , составить выборочное уравнение прямой линии регрессии У на Х (построить график, где отметить точки выборки), проверить гипотезу о значимости коэффициента корреляции.

«Образованный человек тем и отличается от необразованного, что продолжает считать своё образование незаконченным».

Константин Симонов.

Решение. Подсчитываем количество букв и количество гласных букв в каждом слове данного изречения и составляем выборку:

Объём выборки n = 11.

Находим выборочные средние 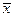, , и выборочные дисперсии , .

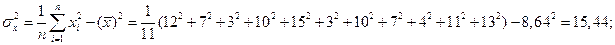
Определим выборочный коэффициент корреляции:

Выборочное уравнение прямой линии регрессии У на Х определяем воспользовавшись формулой:

Рис. 6

На рис. 6 изображен график выборочного уравнения прямой линии регрессии У на Х, а также нанесены точки заданной двумерной выборки.

Для проверки гипотезы о значимости выборочного коэффициента корреляции. Вычисляем наблюдаемое значение критерия:

По таблице приложения для уровня значимости и числу степеней свободы находим критическую точку распределения Стьюдента двухсторонней критической области:

Поскольку то нулевую гипотезу отвергаем и поэтому выборочный коэффициент корреляции значимо отличается от нуля, т. е. Х и У коррелированны.

Ответ: выборочный коэффициент корреляции значимо отличается от нуля.

Не нашли, что искали? Воспользуйтесь поиском: