Образец выполнения задания 3. Задача.Найти выборочное уравнение прямой линии регрессии

Задача. Найти выборочное уравнение прямой линии регрессии

(*)

У на Х по данным корреляционной табл. 1.

Таблица 1

Х У	20 25 30 35 40
	4 6 8 10 32 3 9 4 12 6 1 5
	4 14 46 16 20	=100

Решение. Составим корреляционную табл. 2 в условных вариантах, выбрав в качестве ложных нулей С₁=30 и С₂=36 (каждая из этих вариант расположена в середине соответствующего вариационного ряда):

Таблица 2

	-2 -1 0 1 2
-2 -1	4 6 8 10 32 3 9 4 12 6 1 5
	4 14 46 16 20	=100

Найдем и :

Найдем вспомогательные величины и :

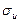Найдем и :

Найдем , для чего составим расчетную табл.3:

Таблица 3

	-2	-1
-2	-8 -8	-6 -12				-14
-1		-8 -8	-10			-8
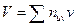
	-8	-20	-6
							контроль

Суммируя числа последнего столбца табл. 3, находим:

.

Для контроля вычислений находим сумму чисел последней строки:

Совпадение сумм свидетельствует о правильности вычислений.

Указания к составлению таблицы 3. Произведение частоты 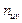на варианту , т.е. , записывают в правом верхнем углу клетки, содержащей частоту. Например, в правых верхних углах клеток первой строки записаны произведения: 4•(-2)=-8, 6•(-1)=-6.

Складывают все числа, помещенные в правых верхних углах клеток одной строки и их сумму помещают в клетку этой же строки «столбца ». Например, для первой строки: =-8+(-6)=-14.

Наконец, умножают варианту на полученное произведение записывают в соответствующую клетку «столбца ». Например, в первой строке таблицы =-2, =-14; следовательно, =(-2)•(-14)=28.

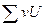Сложив все числа «столбца », получают сумму , которая равна искомой сумме . Например, для табл. 3 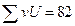, следовательно, искомая сумма

Для контроля расчета аналогичные вычисления производят по столбцам: произведения записывают в левый нижний угол клетки, содержащей частоту; все числа, помещенные в левых нижних углах одного столбца, складывают и их сумму помещают в «строку »; наконец, умножают каждую варианту на и результат записывают в клетках последней строки. Сложив все числа последней строки, получают сумму , которая также равна искомой сумме . Например, для табл. 3: следовательно,

Найдем искомый выборочный коэффициент корреляции:

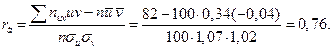
Найдем шаг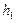и и (разность между любыми двумя соседними вариантами):

Найдем 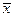и учитывая, что

Найдем и :

Подставив найденные величины в соотношение (*), получим искомое уравнение прямой линии регрессии У на Х:

или окончательно

Не нашли, что искали? Воспользуйтесь поиском: