
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Элементы теории вероятностей.
351-360. Найти вероятности указанных событий, пользуясь правилами сложения и умножения вероятностей.
351. Три стрелка производят по одному выстрелу в цель независимо друг от друга. Вероятности попадания в цель для каждого из них равны соответственно 0,7; 0,8; 0,9. Найти вероятность того, что: а) в цель попадает только один стрелок; б) в цель попадают только два стрелка; в) в цель попадает хотя бы один стрелок.
352. Вероятность выполнения плана бригадами соответственно равна 0,8 и 0,9. Найти вероятность того, что выполнят план: а) обе бригады; б) хотя бы одна бригада; в) только одна бригада.
353. Всхожесть семян первого, второго и третьего сортов некоторой культуры составляет соответственно 90%; 80% и 70%. Вычислить вероятность того, что из трех посеянных разносортных семян этой культуры: а) взойдут все три; б) взойдет только одно; в) взойдет хотя бы одно.
354. Для сигнализации об аварии установлены три независимо работающих датчика. Вероятность исправной работы 1-го датчика равна 0,9, второго 0,95, третьего 0,8. Найти вероятность того, что: а) сработает только один датчик; б) сработает только два датчика; в) сработает хотя бы один датчик.
355. Рабочий обслуживает три станка. Вероятность бесперебойной работы в течение месяца для первого станка равна 0,8, для второго – 0,9, для третьего – 0,8. Найти вероятность того, что в течение месяца без остановки будут работать: а) все станки; б) только два станка; в) хотя бы один станок.
356. Вероятность установления в данной местности устойчивого снежного покрова с октября равна 0,1. Определить вероятность того, что в ближайшие три года в этой местности устойчивый снежный покров с октября: а) не установится ни разу; б) установится хотя бы один раз; в) установится два раза.
357. Исследователь разыскивает нужные ему сведения в трех справочниках. Вероятности того, что эти сведения находятся в первом, во втором и третьем справочниках равны соответственно 0,7; 0,6 и 0,9. Найти вероятность того, что требуемые сведения содержатся: а) только в одном справочнике; б) хотя бы в одном справочнике; в) во всех справочниках.
358. Всхожесть фасоли 80%, гороха 90%, бобов 70%. Определить вероятность того, что из трех посеянных семян различных культур: а) взойдут два; б) не взойдет ни одного; в) взойдет хотя бы одно.
359. Вероятность выхода из строя станка в течение одного рабочего дня равна 0,1. Какова вероятность того, что за три рабочих дня станок: а) ни разу не выйдет из строя; б) выйдет только один раз; в) выйдет хотя бы один раз.
360. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что наугад взятое изделие окажется бракованным, равна 0,15. Проверено три изделия. Какова вероятность того, что среди них бракованных: а) все три; б) только два; в) хотя бы одно.
361-370. Найти вероятности указанных событий, пользуясь формулами полной вероятности и Байеса.
361. На одном заводе на каждые 100 лампочек приходится в среднем 10 нестандартных, на втором – 15, а на третьем – 20. Продукция этих заводов составляет соответственно 50; 30 и 20% всех электролампочек, приобретаемых жителями района.
1) Найти вероятность того, что приобретенная лампочка будет стандартной.
2) Приобретенная лампочка оказалась стандартной. Какова вероятность того, что эта лампочка изготовлена на первом заводе?
362. Всхожесть семян свеклы первой партии 90%, второй партии – 80%. Перед посевом смешали 2 ц семян 1-ой партии и 3 ц семян 2-ой партии.
1) Какова будет вероятность всхода, если наугад посадили одно семя?
2) Семя взошло. Какова вероятность того, что оно из 1-ой партии?
363. На фабрике на машинах A, B, C производят соответственно 25; 35 и 40% всех изделий. В их продукции брак составляет соответственно 15; 10 и 5%.
1) Найти вероятность того, что случайно выбранное изделие окажется дефектным.
2) Выбранное изделие оказалось дефектным. Найти вероятность того, что оно изготовлено на машине A.
364. На спартакиаду прибыло 20 лыжников, 15 гимнастов и 5 шахматистов. Вероятность выполнить квалификационную норму такова: для лыжника – 0,8; для гимнаста – 0,6; для шахматиста – 0,9. Случайно вызывается один спортсмен.
1) Какова вероятность того, что он выполнит норму?
2) Спортсмен выполнил норму. Какова вероятность того, что это был шахматист?
365. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 3% брака, второй – 2%, а третий – 4%.
1) Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго – 2000 и с третьего – 2500 деталей.
2) Деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем автомате.
366. Три оператора радиолокационной установки производят соответственно 25; 30 и 40% всех измерений, допуская 5, 4 и 3% ошибок.
1) Найти вероятность того, что случайно проверенное измерение окажется ошибочным.
2) Измерение оказалось ошибочным. Найти вероятность того, что оно произведено первым оператором.
367. На ферме содержатся 40% коров костромской породы и 60% башкирской. В районе эпидемия ящура. Вероятность заболеть ящуром у коров костромской породы 0,6; у коров башкирской породы – 0,7. Для обследования случайным образом взята одна корова.
1) Найти вероятность того, что она больна ящуром.
2) Корова оказалась больна. Какова вероятность того, что она башкирской породы.
368. В засуху растение погибает с вероятностью 0,9. Без засухи выживаемость растения составляет 95%. Вероятность засухи в году данной местности 0,2.
1) Найти вероятность выживания растения в данном году.
2) Растение выжило. Найти вероятность того, что засухи не было.
369. Имеется два мешка семян одной культуры первой партии, всхожестью 90% и один мешок той же культуры второй партии, всхожестью 85%. Наугад взяли мешок и посадили одно зерно.
1) Какова вероятность того, что оно взойдет?
2) Зерно взошло. Какова вероятность того, что оно из первой партии?
370. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше, чем второго. Из ящика наудачу взята одна деталь.
1) Какова вероятность того, что деталь будет бракованной?
2) Деталь оказалась бракованной. Какова вероятность того, что она произведена на первом станке?
371-380. Рабочий изготовляет за смену n деталей. Вероятность того, что деталь окажется первого сорта, равна p. Какова вероятность того, что деталей первого сорта будет ровно k штук?
371. n=400; р=0,8; k=330 372. n=400; р=0,9; k=372
373. n=300; р=0,75; k=240 374. n=600; р=0,6; k=375
375. n=625; р=0,64; k=370 376. n=192; р=0,75; k=150
377. n=225; р=0,8; k=165 378. n=100; р=0,9; k=96
379. n=150; р=0,6; k=75 380. n=625; р=0,8; k=510
381-390. Вероятность появления события А в каждом из n независимых испытаний р. Найти вероятность того, что в этих испытаниях событие А появится от k1 до k2 раз.
381. n=150; р=0,6; k1=78 k2=96
382. n=100; р=0,8; k1=72 k2=84
383. n=400; р=0,9; k1=345 k2=372
384. n=600; р=0,4; k1=210 k2=252
385. n=300; р=0,75; k1=210 k2=225
386. n=625; р=0,36; k1=225 k2=255
387. n=400; р=0,5; k1=190 k2=215
388. n=225; р=0,2; k1=45 k2=60
389. n=300; р=0,25; k1=75 k2=90
390. n=625; р=0,64; k1=400 k2=430
391-400. Составить ряд распределения для случайной величины Х – числа бракованных деталей в выборке объема n. Вероятность того, что деталь окажется бракованной, равна р. Определить вероятность того, что в выборке будет бракованных: 1) ровно k деталей; 2) более k деталей; 3) не более k деталей. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
391. n=4; р=0,8; k=2. 392. n=3; р=0,1; k=2.
393. n=5; р=0,2; k=3. 394. n=3; р=0,7; k=2.
395. n=6; р=0,1; k=4. 396. n=4; р=0,3; k=2.
397. n=5; р=0,3; k=4. 398. n=3; р=0,9; k=3.
399. n=4; р=0,8; k=3. 400. n=5; р=0,2; k=4.
401-410. Две независимые дискретные случайные величины Х и У заданы своими законами распределения. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z=3Х–2Y.
401.
| Х | – 6 | Y | –8 | |||||
| Р | 0,1 | 0,1 | 0,6 | 0,2; | P | 0,4 | 0,6. |
402.
| Х | –2 | –1 | Y | –3 | ||||
| Р | 0,2 | 0,5 | 0,1 | 0,2; | P | 0,3 | 0,7. |
403.
| Х | – 5 | –4 | –2 | Y | –8 | –1 | ||
| Р | 0,1 | 0,5 | 0,2 | 0,2; | P | 0,7 | 0,3. |
404.
| Х | – 6 | –3 | Y | –2 | ||||
| Р | 0,3 | 0,3 | 0,2 | 0,2; | P | 0,2 | 0,8. |
405.
| Х | −4 | –2 | –1 | Y | –3 | –1 | ||
| Р | 0,1 | 0,3 | 0,2 | 0,4; | P | 0,4 | 0,6. |
406.
| Х | –2 | Y | ||||||
| Р | 0,5 | 0,1 | 0,2 | 0,2; | P | 0,2 | 0,8. |
407.
| Х | –7 | –5 | -2 | Y | –3 | |||
| Р | 0,4 | 0,4 | 0,1 | 0,1; | P | 0,1 | 0,9. |
408.
| Х | –1 | Y | –2 | |||||
| Р | 0,2 | 0,5 | 0,1 | 0,2; | P | 0,8 | 0,2. |
409.
| Х | –8 | –6 | –1 | Y | ||||
| Р | 0,5 | 0,1 | 0,2 | 0,2; | P | 0,2 | 0,8. |
410.
| Х | –2 | Y | ||||||
| Р | 0,1 | 0,1 | 0,3 | 0,5; | P | 0,1 | 0,9. |
411-420. Случайная величина Х задана функцией распределения вероятностей F(х). Найти: а) вероятность попадания случайной величины Х в интервал 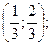 б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
б) плотность распределения вероятностей случайной величины Х; в) математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Х.
411.  412.
412. 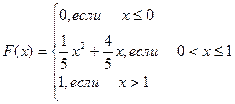
413. 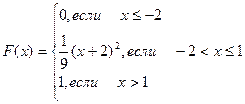 414.
414. 
415. 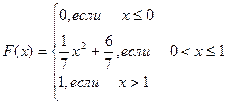 416.
416. 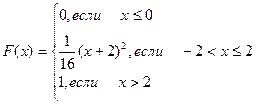
417.  418.
418. 
419. 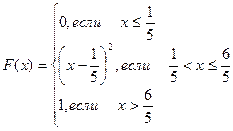 420.
420. 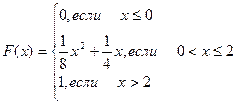
421-430. Случайные отклонения размера детали от номинала распределены нормально; математическое ожидание размера детали равно М(Х), среднее квадратическое отклонение s(Х). Годными считаются детали, размер которых заключен между α и β. Определить 1) вероятность изготовления годной детали; 2) процент бракованных деталей, если точность изготовления ухудшится и будет характеризоваться средним квадратическим отклонением s1(х).
Данные к задачам 421- 430
| Номер задачи | ||||||||||
| М(Х) | ||||||||||
| s(х) | 0,8 | 0,5 | 0,4 | 0,9 | 0,3 | 0,1 | 0,2 | 0,6 | 0,7 | 0,8 |
| α | 239,5 | 299,7 | ||||||||
| β | 240,5 | 350,2 | 399,6 | |||||||
| s1(х) | 0,6 | 0,5 | 0,93 | 0,35 | 0,2 | 0,4 | 0,66 | 0,77 | 0,9 |
431- 440. Найти математическое ожидание и дисперсию дискретной случайной величины Х.
431. В коробке среди 5 деталей две окрашенные. Детали извлекаются последовательно до извлечения обеих окрашенных деталей, после чего извлечение прекращается. Х – число извлеченных деталей.
432. Стрелок выстрелил 3 раза по удаляющейся мишени. Вероятность попадания в нее при первом выстреле равна 0,8, а с каждым следующим выстрелом она уменьшается на 0,1. Х - число попаданий в цель.
433. В партии 10 деталей, 3 из них нестандартных. Наугад отобраны 2 детали. Х – число нестандартных деталей среди 2 отобранных.
434. Из 25 контрольных работ, среди которых 5 оценены на 5, наугад извлекаются 3 работы. Х - число работ, оцененных на 5 и оказавшихся в выборке.
435. Вероятность отказа детали за время испытания на надежность равна 0,2. Испытанию подвергнуты 10 деталей. Х - число отказавших деталей.
436.Одновременно подбрасываются две игральные кости. Х - произведение числа очков, которые могут выпасть при одном бросании.
437.Производятся 3 выстрела с вероятностями попадания в цель, равными 0,4; 0,3; 0,6. Х - общее число попаданий
438.Вероятность выигрыша по одному лотерейному билету равна 0,3. Приобретено 20 билетов. Х - число лотерейных билетов, на которые выпадут выигрыши.
439.Проводится 100 независимых испытаний, в каждом из которых вероятность наступления события равна 0,7. Х - число появлений события в этих испытаниях.
440.Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа приборов - 0,3; 0,4; 0,5; 0,6. Х - число отказавших приборов.
441- 450. Проводится n независимых испытаний, в каждом из которых событие А имеет постоянную вероятность р1 т.е. Р(А)=р. Найти вероятность того, что при n испытаниях событие А наступит m раз (Рn (m)). Вероятность Рn (m) найти двумя способами: а) по формуле Бернулли, б) с помощью локальной теоремы Лапласа.
441. Всхожесть семян ржи составляет 90%. Найти вероятность того, что из 18 посеянных семян взойдет 10, т.е. Р18 (10).
442. Стрелок сделал 20 выстрелов с вероятностью попадания при отдельном выстреле 0,4. Найти вероятность того, что при этом будет 12 попаданий, т.е. Р20 (12).
443. Вероятность рождения мальчика равна 0,51. Найти вероятность того, что среди 30 новорожденных окажется 15 мальчиков, т.е. Р30 (15).
444. Вероятность изготовления детали высшего сорта на данном станке равна 0,4. Найти вероятность того, что среди наудачу взятых 19 деталей 9 окажется высшего сорта, т.е. Р19 (9).
445. Игральная кость бросается 20 раз.. Найти вероятность того, что при этом 3 очка выпадет 12 раз, т.е. Р20 (12).
446. Баскетболист бросает мяч в кольцо 24 раз.. Какова вероятность того, что при этом будет 15 попаданий, если вероятность попадания в кольцо при одиночном броске равна 0,7, т.е. Р24 (15).
447. Вероятность выигрыша по одному билету денежно-вещевой лотереи равна 0,3.
Какова вероятность того, что из 26 приобретенных билетов 10 окажутся выигрышными, т.е. Р26 (10).
448.В урне 3 шара: белый, черный, красный. Из урны извлекают один шар и затем возвращают обратно. Этот опыт повторяется 25 раз. Найти вероятность того, что белый шар будет извлечен 18 раз, т.е. Р25 (18).
449.В урне 5 шаров: 1 белый, 2 черных, 2 красных. Из урны извлекают два шара и затем возвращают их обратно. Этот опыт повторяется 18 раз. Найти вероятность того, что разноцветные шары будут извлекаться 10 раз, т.е. Р18 (10).
450.В коробке среди 5 деталей - 3 окрашенные. Детали извлекаются по одному и затем возвращаются обратно. Этот опыт повторяется 20 раз. Найти вероятность того, что в результате такого опыта неокрашенные детали будут извлекаться 16 раз, т.е. Р20 (16).
451-460. Для случайной величины Х заданы функции распределения F(x) или плотность вероятности φ(х). Найти числовые характеристики Х, построить график F(x) или φ(х), найти вероятность попадания значения Х в заданный интервал и др.
451. Дана функция распределения F(x) непрерывной случайной величины Х

Найти плотность вероятности φ(х), P  , M(Х), D(X), начертить графики
, M(Х), D(X), начертить графики 
452. Случайная величина X задана плотностью вероятности
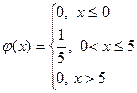
Найти функцию распределения F(x),  , M(Х), D(X), начертить графики
, M(Х), D(X), начертить графики 
453. Для непрерывной случайной величины X задана функция распределения
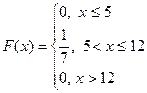
Найти плотность вероятности j (x), 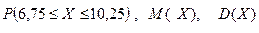 , начертить графики
, начертить графики 
454. Плотность вероятности непрерывной случайной величины X имеет вид

Найдите значение параметра m, функцию распределения F(x), M(Х), D(X), 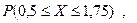 начертить графики
начертить графики 
455. Для случайной величины X задана плотность вероятности
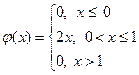
Найти функцию распределения F(x),  построить графики
построить графики
j (x) и F(x).
456. Непрерывная случайная величина X задана функцией распределения

Найти плотность вероятности j (x), 
457. Дана плотность вероятности для случайной величины X
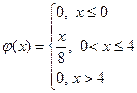
Найти M(X), D(X), s(X), функцию распределения F(X), построить графики j (x) и F(x).
458. Случайная величина Х задана посредством плотности вероятности.

Найти функцию распределения F(X), M(X), D(X),  , построить графики j (x) и F(x).
, построить графики j (x) и F(x).
459. Непрерывная случайная величина X задана функцией распределения

Найти плотность вероятности j (x), 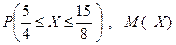 , построить графики j (x) и F(x).
, построить графики j (x) и F(x).
460. Для непрерывной случайной величины X задана функция распределения

Найти плотность вероятности j (x), 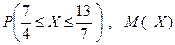 , построить графики j (x) и F(x).
, построить графики j (x) и F(x).
461-470.Разные задачи по теории вероятностей.
461.Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует все патроны). Найти математическое ожидание и дисперсию случайной величины Х− числа израсходованных патронов. Построить график функции распределения этой случайной величины, если вероятность попадания при каждом выстреле равна 0,25.
462. Функция распределения F(x) непрерывной случайной величины X имеет вид
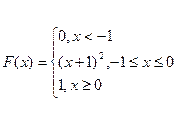
Найти M(X), D (X) и вероятность того, что при каждом из трёх независимых наблюдений этой случайной величины будет выполнено условие X<-1/2.
463. Каждая из пяти упаковок тетрадей содержит две тетради в линейку и три- в клетку. Из каждой упаковки случайным образом отбираются по две тетради. Найти вероятность того, что не менее чем в трёх из отобранных пяти пар тетрадей обе тетради будут в клетку.
464. Три стрелка независимо друг от друга стреляют по одной цели. Вероятность попадания первого стрелка в цель равна 0,7, второго – 0,8, третьего—0,9. Составить таблицу распределения X –числа попаданий в цель, найти его математическое ожидание, дисперсию, построить функцию распределения и её график.
465. В первой урне 2 белых и 3 черных шара, во второй- 2 белых и 2 черных шара, в третьей - 3 белых и 1 черный. Из первой урны переложили один шар во вторую урну, затем из второй урны один шар - в третью урну и после этого из третьей урны один шар в первую урну. Найти вероятность того, что состав шаров в урнах не изменится.
466. Снаряд уничтожает цель с вероятностью 0,8. Сколько надо выпустить снарядов по цели, чтобы уничтожить цель с вероятностью 0,99?
467. В первой урне содержится 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взяли один шар. Найти вероятность того, что взят белый шар.
468.Случайная величина x задана функцией распределения F(x), график которой имеет вид
 F(x)
F(x)


 1
1
 х
х
0 1 2 3 4
Найти P(Х<0.3), P(Х<3,5), P(Х³3,5), P(Х³6), M(Х), D(Х).
469.Имеется 9урн, из них в трех по 5белых и 4черных шара, в двух - по 2белых и 3 черных шаров,в четырех –по 4 белых и 8 черных шара.Из наугад выбранной урны извлечен один шар. Найти вероятность того, что шар извлечен из урны второго состава, если он оказался черным.
470. Плотность распределения непрерывной случайной величины X имеет вид

Найти значение параметра а, если M(Х)=1. Вычислить Р(Х>2), D(Х).
Не нашли, что искали? Воспользуйтесь поиском: