Определение вектора. Линейные операции над векторами.

Вектором называется направленный отрезок, т.е. отрезок, имеющий определённую длину и определённое направление.

Под линейными операциями над векторами понимают:

а) произведение вектора на число;

б) сложение и вычитание векторов.

Произведением вектора на число lÎR наз. вектор l , удовлетворяющий следующим условиям:

1) длина вектора l равна произведению модуля числа l на длину вектора : ;

2) вектор l коллинеарен вектору : направление вектора l совпадает с направление вектора , если l>0, и противоположно ему, если l<0.

Сложение двух векторов можно производить по правилам:

1) параллелограмма;

2) треугольника.

Правило параллелограмма. Пусть даны два произвольных вектора :

Выберем произвольную точку О и перенесём векторы так, чтобы их начало оказалось в точке О.

Правило треугольника. Пусть – два произвольных вектора. Возьмём произвольную точку О и построим вектор . От точки А отложим вектор . Вектор 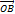, соединяет начало первого вектора с концом второго наз. суммой векторов . .

Сложение трёх и более векторов можно находить по правилу замыкания ломаной. Чтобы найти сумму векторов , нужно конец вектора совместить с началом вектора , конец вектора , совместить с началом вектора 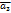и т. д. пока не дойдём до вектора . Тогда суммой будет вектор идущий из начала вектора в конец вектора .

Разностью двух векторов называется такой вектор , который нужно сложить с вектором , чтобы получить вектор , т.е. Û .

Чтобы построить вектор равный нужно параллельным переносом перенести вектор 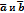к общему началу, и тогда вектор будет выходить из конца вектора в конец вектора .

В параллелограмме, построенном на векторах одна направленная диагональ является суммой векторов, а другая разностью.

Не нашли, что искали? Воспользуйтесь поиском: