
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Т - критерий Вилкоксона
Назначение критерия
Критерий применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых.
Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более интенсивным чемв другом.
Описание критерия Т
Этот критерий применим в тех случаях, когда признаки измерены по крайней мере по шкале порядками сдвиги между вторым и первым замерами тоже могут быть упорядочены. Для этого они должны варьировать в достаточно широком диапазоне.
Гипотезы
Но: Интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении.
H1: Интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в нетипичном направлении.
Ограничения в применении критерия Т Вилкоксона
1. Минимальное количество испытуемых, прошедших измерения в двух условиях - 5 человек. Максимальное количество испытуемых - 50 человек, что диктуется верхней границей имеющихся таблиц. Критические значения Т приведены в Табл. VI Приложения 1.
2. Нулевые сдвиги из рассмотрения исключаются, и количество наблюдений n уменьшается на количество этих нулевых сдвигов (McCall R., 1970, р. 36). Можно обойти это ограничение, сформулировав гипотезы, включающие отсутствие изменений, например: "Сдвиг в сторону увеличения значений превышает сдвиг в сторону уменьшения значений и тенденцию сохранения их на прежнем уровне".
Пример
В выборке курсантов военного училища (юноши в возрасте от 18 до 20 лет) измерялась способность к удержанию физического волевого усилия на динамометре. Сначала у испытуемых измерялась максимальная мышечная сила каждой из рук, а на следующий день им предлагалось выдерживать, на динамометре с подвижной стрелкой мышечное усилие, равное 1/2 максимальной мышечной силы данной руки. Почувствовав усталость, испытуемый должен был сообщить об этом экспериментатору, но не прекращать опыт, преодолевая усталость и неприятные ощущения - "бороться, пока воля не иссякнет". Опыт проводился дважды; вначале с обычной инструкцией, а затем, после того, как испытуемый заполнял опросник самооценки волевых качеств по методике А.Ц. Пуни (Пуни А.Ц., 1977), ему предлагалось представить себе, что он уже добился идеала в развитии волевых качеств, и продемонстрировать соответствующее идеалу волевое усилие. Подтвердилась ли гипотеза экспериментатора о том, что обращение к идеалу способствует возрастанию волевого усилия? Данные представлены в Табл. 3.5.
Таблица 3.5
Расчет критерия Т при сопоставлении замеров физического волевого усилия.
| Код имени | Длительность удержания усилия на динамометре (с) | Разность (tпосле - tдо) | Абсолютное значение разности | Ранговый номер разности | ||
| До измерения воле-вых качеств и обра-щения к идеалу (tдо ) | После измерения волевых качеств и обращения к идеалу (tпосле) | |||||
| Г. | -39 | |||||
| Кос | -27 | |||||
| 3. | Крив. | 74 | 77 | +3 | 3 | 1 |
| Кур. | -19 | |||||
| 5. | Л. | -38 | 9,5 | |||
| 6. | М. | -8 | ||||
| 7. | Р. | 73 | 77 | +4 | 4 | 2,5 |
| 8. | С. | -4 | 2,5 | |||
| Т. | -38 | 9,5 | ||||
| 10. | Х. | 97 | 122 | +25 | 25 | 7 |
| Ю. | -18 | |||||
| Сумма |
Для подсчета этого критерия нет необходимости упорядочивать ряды значений по нарастанию признака. Мы можем использовать алфавитный список испытуемых, как в данном случае.
Первый шаг в подсчете критерия Т - вычитание каждого индивидуального значения "до" из значения "после". Можно вычитать значения "после" из значений "до", это никак не повлияет на расчет критерия. Но лучше во всех случаях придерживаться одной системы, чтобы не запутаться самим.
Мы видим из Табл. 3.5, что 8 полученных разностей - отрицательные и лишь 3 - положительные. Это означает, что у 8 испытуемых длительность удержания "мышечного усилия во втором замере уменьшилась, а у 3 - увеличилась. Мы столкнулись с тем случаем, когда уже сейчас мы не можем сформулировать статистическую гипотезу, соответствующую первоначальному предположению исследователя. Предполагалось, что обращение к идеалу будет увеличивать длительность мышечного усилия, а экспериментальные данные свидетельствуют, что лишь в 3 случаях из 11 этот сказатель действительно увеличился. Мы можем сформулировать лишь гипотезу, предполагающую несущественность сдвига этого показателя в сторону снижения.
Сформулируем гипотезы.
Но: Интенсивность сдвигов в сторону уменьшения длительности мышечного усилия не превышает интенсивности сдвигов в сторону ее увеличения.
Н1:Интенсивность сдвигов в сторону уменьшения длительности мышечного усилия превышает интенсивность сдвигов в сторону ее увеличения
На следующем шаге все сдвиги, независимо от их знака, должны быть проранжированы по выраженности. В Табл. 3.5 в четвертом слева столбце приведены абсолютные величины сдвигов, а в последнем столбце (справа) - ранги этих абсолютных величин. Меньшему значению соответствует меньший ранг. При этом сумма рангов равна 66, что соответствует расчетной:
N ∙ (N+1) 11 ∙ (11+1)
∑Ri = ─────── = ─────── = 66
2 2
Теперь отметим те сдвиги, которые являются нетипичными, в данном случае - положительными. В Табл. 3.5 эти сдвиги и соответствующие им ранги выделены цветом. Сумма рангов этих "редких" сдвигов и составляет эмпирическое значение критерия Т:
∑Rr
где R r - ранговые значения сдвигов с более редким знаком. Итак, в данном случае, Тэмп=1+2,5+7=10,5
По Таблице VI Приложения 1 определяем критические значения Т для n=11:
Ткр = 13 (р ≤0,05) 7 (р ≤0,01)
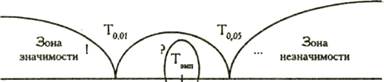
7 10,5 13
Зона значимости в данном случае простирается влево. Действительно, если бы "редких", в данном случае положительных, сдвигов не было совсем, то и сумма их рангов равнялась бы нулю. В данном же случае эмпирическое значение Т попадает в зону неопределенности:
Твмп<Ткр (0,05)
Ответ: Но отвергается. Интенсивность отрицательного сдвига показателя физического волевого усилия превышает интенсивность положительного сдвига (р<0,05).
АЛГОРИТМ 9
Подсчет критерия Т Вилкоксона
1. Составить список испытуемых в любом порядке, например, алфавитном.
I. Вычислить разность между индивидуальными значениями во втором и первом замерах ("после" - "до"). Определить, что будет считаться "типичным" сдвигом и сформулировать соответствующие гипотезы.
3.Перевести разности в абсолютные величины и записать их отдельным столбцом (иначе трудно отвлечься от знака разности).
4. Проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг. Проверить совпадение полученной суммы рангов с расчетной.
5.Отметить кружками или другими знаками ранга, соответствующие сдвигам в "нетипичном" направлении.
6.Подсчитать сумму этих рангов по формуле:
T=∑Rr
где Rr - ранговые значения сдвигов с более редким знаком.
7. Определить критические значения Т для данного п по Табл. VI Приложения 1. Если Т меньше или равен Т, сдвиг в "типичную" сторону по интенсивности достоверно преобладает.
Критерий Пирсона
Назначения критерия
Критерий χ2применяется в двух целях:
1)для сопоставления эмпирического распределения признака с теоретическим - равномерным, нормальным или каким-то иным; 2)для сопоставления двух, трех или более эмпирических распределений одного и того же признака1. 1На самом деле области применения критерия χ2многообразны (см., например: Суходольский Г.В.. 1972, с. 295), но в данном руководстве мы ограничиваемся только этими двумя, наиболее часто встречающимися на практике, целями.
Описание критерия
Критерий χ2 отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях.
Преимущество метода состоит в том, что он позволяет сопоставлять распределения признаков, представленных в любой шкале, начиная от шкалы наименований (см. п. 1.2).
Чем больше расхождение между двумя сопоставляемыми распределениями, тем больше эмпирическое значение χ2.
Гипотезы
Возможны несколько вариантов гипотез, в зависимости от задач, которые мы перед собой ставим.
Первый вариант:
Но: Полученное эмпирическое распределение признака не отличается от теоретического (например, равномерного) распределения.
H1: Полученное эмпирическое распределение признака отличается от теоретического распределения.
Второй вариант:
Но: Эмпирическое распределение 1 не отличается от эмпирического распределения 2.
H1:Эмпирическое распределение 1 отличается от эмпирического распределения 2.
Третий вариант:
Но: Эмпирические распределения 1, 2, 3,... не различаются между собой.
H1: Эмпирические распределения 1, 2, 3,... различаются между собой.
Критерий χ2 позволяет проверить все три варианта гипотез.
Ограничения критерия
1. Объем выборки должен быть достаточно большим: n>30. При n<30 критерий χ2 дает весьма приближенные значения. Точность критерия повышается при больших n.
2. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: f>5. Это означает, что если число разрядов задано заранее и не может быть изменено, то мы не можем применять метод χ2, не накопив определенного минимального числа наблюдений. Если, например, мы хотим проверить наши предположения о том, что частота обращений в телефонную службу Доверия неравномерно распределяются по 7 дням недели, то нам потребуется 5-1=35 обращений. Таким образом, если количество разрядов (k) задано заранее, как в данном случае, минимальное число наблюдений (nmin) определяется по формуле: nmin = k∙5.
3.Выбранные разряды должны "вычерпывать" все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопоставляемых распределениях.
4. Необходимо вносить "поправку на непрерывность" при сопоставлении распределений признаков, которые принимают всего 2 значения. При внесении поправки значение χ2уменьшается (см. Пример С поправкой на непрерывность).
5.Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду.
Сумма наблюдений по разрядам всегда должна быть равна общему количеству наблюдений.
Шутливый пример
В гениальной комедии Н. В. Гоголя "Женитьба" у купеческой дочери Агафьи Тихоновны было пятеро женихов. Одного она сразу исключила из рассмотрения, потому что он был купеческого звания, как и она сама. А из остальных она не знала, кого выбрать: "Уж как трудно решиться, так просто рассказать нельзя, как трудно. Если бы губы Никанора Ивановича да приставить к носу Ивана Кузьмича, да взять сколько-нибудь развязности, какая у Балтазара Балтазарыча, да, пожалуй, прибавить к этому еще дородности Ивана Павловича, я бы тогда тотчас решилась. А теперь поди подумай! просто голова даже стала болеть. Я думаю, лучше всего кинуть жребий" (Гоголь Н.В., 1959, с. 487). И вот Агафья Тихоновна положила бумажки с четырьмя именами в ридикюль, пошарила рукою в ридикюле и вынула вместо одного — всех!
Ей хотелось, чтобы жених совмещал в себе достоинства всех четверых, и, вынимая все бумажки вместо одной, она бессознательно совершала процедуру выведения средней величины. Но вывести среднюю величину из четверых людей невозможно, и Агафья Тихоновна в смятении. Она влюблена, но не знает, в кого. "Такое несчастное положение девицы, особливо ещевлюбленной" (там же, с. 487).
Вся беда в том, что ни Агафья Тихоновна, ни ее тетушка, ни сваха Фекла Ивановна не были знакомы с критерием χ2. Именно он мог бы им помочь в решении их проблемы. С его помощью можно было бы попробовать установить, в кого больше влюблена Агафья Тихоновна.
Второй вариант развития шутливого примера: сопоставление двух эмпирических распределений
Теперь мы должны ответить на вопрос, одинаковая ли система предпочтений проявляется во взгляде Агафьи Тихоновны и ее словах?
Сформулируем гипотезы.
Но: Распределения невербально и вербально выражаемых предпочтений не различаются между собой.
H1: Распределения невербально и вербально выражаемых предпочтений различаются между собой.
Для подсчета теоретических частот нам теперь придется составить специальную таблицу (Табл. 4.5). Ячейки в двух столбцах слева обозначим буквами. Для каждой из них теперь будет подсчитана особая, только к данной ячейке относящаяся, теоретическая частота. Это обусловлено тем, что количества взглядов и словесных отзывов невесты о женихах неравны; взглядов 32, а словесных отзывов - 36. Мы должны всякий раз учитывать эту пропорцию.
Таблица 4.5
Эмпирические и теоретические частоты взглядов и упоминаний о женихах
| Разряды - женихи | Эмпирические частоты | Суммы | Теоретические частоты | ||
| Взгляда | Упоминаний в разговоре | Взгляда | Упоминаний в разговоре | ||
| 1.Ник. Ив. 2.Ив. Куз. 3.Ив. Пав. 4.Бал. Бал. | 14 А 5 В 8 Д 5 Ж | 15 Б 6 Г 9 Е 6 3 | 13,63 А 5,17 В 7,99Д 5,17 Ж | 15,37 Б 5,83 Г 9,01 Е 5,83 3 | |
| Суммы |
Рассчитаем эту пропорцию. Всего проявлений благосклонности отмечено 68, из них 32 - взгляды и 36 - словесные высказывания. Доля взглядов составит 32/68=0,47; доля упоминаний - 36/68=0,53.
Итак, во всех строках взгляды должны были бы составлять 0,47 всех проявлений по данной строке, а упоминания в разговоре - 0,53 всех проявлений. Теперь, зная суммы проявлений по каждой строке, мы можем рассчитать теоретические частоты для каждой ячейки Табл. 4.5.
ƒАтеор=29∙0,47=13,63
ƒАтеор =29∙0,53=15,37
ƒ Втеор =11∙0,47=5,17
ƒГтеор=11∙0,53=5,83
ƒДтеор=17∙0,47=7,99
ƒЕтеор=17∙0,53=9,01
ƒЖтеор=11∙0,47=5,17
ƒЗтеор=11∙0,53=5,83
Ясно, что сумма теоретических частот по строкам будет равняться сумме всех проявлений по данной строке. Например,
ƒАтеор + ƒАтеор =13,63+15,37=29
ƒ Втеор + ƒГтеор =5,17+5,83=11
ƒДтеор + ƒЕтеор =7.99+9.01=17 и т.д.
При такого рода подсчетах лучше всякий раз себя проверить. Теперь мы можем вывести общую формулу подсчета ƒтеор для сопоставления двух или более эмпирических распределений:

Соответствующими строкой и столбцом будут та строка и тот столбец, на пересечении которых находится данная ячейка таблицы. Теперь нам лучше всего сделать развертку Табл. 4.5, представив все ячейки от А до Ж в виде первого столбца - это будет столбец эмпирических частот. Вторым столбцом будут записаны теоретические частоты. Далее будем действовать по уже известному алгоритму. В третьем столбце будет представлены разности эмпирических и теоретических частот, в четвертом - квадраты этих разностей, а в пятом - результаты деления этих квадратов разностей на соответствующие каждой строке теоретические частоты. Сумма в нижнем правом углу таблицы и будет представлять собой эмпирическую величину χ2(Табл. 4.6).
Табл. 4.6
Расчет критерия χ2 при сопоставлении распределений невербальных и
вербальных признаков благосклонности невесты
| Ячейки таблицы частот | Эмпирическая частота взгляда (ƒэ) | Теоретическая частота (ƒт) | (ƒэ- ƒт) | (ƒэ- ƒ т)2 | (ƒэ- ƒ т)2 ──────── ƒт | |
| А | 13,63 | +0,37 | 0,14 | 0,01 | ||
| Б | 15,37 | -0,37 | 0,14 | 0,01 | ||
| В | 5,17 | -0,17 | 0,03 | 0,01 | ||
| Г | 5,83 | +0,17 | 0,02 | 0,00 | ||
| Д | 7,99 | +0,01 | 0,00 | 0,00 | ||
| Е | 9,01 | -0,01 | 0,00 | 0,00 | ||
| Ж | 5,17 | -0,17 | 0,03 | 0,01 | ||
| З | 5,83 | +0,17 | 0,02 | 0,00 | ||
| Суммы | 0,04 |
Число степеней свободы при сопоставлении двух эмпирических распределений определяется по формуле:
V= (k-1) ∙ (c-1)
где k - количество разрядов признака (строк в таблице эмпирических частот);
с - количество сравниваемых распределений (столбцов в таблице эмпирических частот).
В данном случае таблицей эмпирических частот является левая, эмпирическая часть таблицы 4.5, а не на ее развертка (Табл. 4.6).
Количество разрядов - это количество женихов, поэтому k=4.
Количество сопоставляемых распределений с=2.
Итак, для данного случая,
v=(4-l)∙(2-l)=3
Определяем по Табл. IX Приложения 1 критические значения
для v=3:
Ответ: 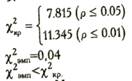
Но принимается. Распределения невербально и вербально выражаемых невестой предпочтений не различаются между собой.
Итак, Агафья Тихоновна весьма последовательна в проявлении своих предпочтений, хотя, по-видимому, сама этого пока не замечает.
Не нашли, что искали? Воспользуйтесь поиском: