Пример выполнения курсового задания С 1

Дано: P = 20 кН; M = 10 кН·м; q = 2 кНм. Определить реакции внешних связей в точках А и В.

Решение.

Определение реакций внешних связей для рассматриваемой балки проводится согласно алгоритму решения задач статики, приведённому в подразделе 1.7.

1. Выбирается система отсчёта. Так как балка плоская, то выбирается система отсчёта OXY.

2. Выделяется тело, равновесие которого рассматривается. В нашем случае таким телом является балка, изображённая на рис. 1.49.

3. К балке прикладываются активные нагрузки. По условию задачи активные нагрузки известны. Так как задана распределённая нагрузка с интенсивностью q, то её приводят к сосредоточенной силе Q, модуль которой определяют по формуле Q = q×L = 2×2 = 4 кН. Эту сосредоточенную силу прикладывают к телу и показывают размер, на котором она приложена. Таким образом, на балку действуют следующие активные нагрузки: P, Q – активные силы; активная пара сил с алгебраическим моментом М.

4. Согласно аксиоме связей внешние связи, наложенные на механическую систему в точках А и В, отбрасывают и показывают реакции внешних связей X _A, Y _A, R _B. Таким образом, на балку действуют внешние нагрузки, состоящие из активных нагрузок: P, Q, M и реакций внешних связей: X _A, Y _A, R _B.

5. Так как система внешних сил, действующих на тело, является плоской и произвольной, то записывают три уравнения равновесия:

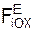Σ + Σ 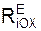= 0 = Q – P·cos(60^о) + X_A = 0; (1)

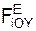Σ + Σ 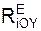= 0 = – P·sin(60^о) + R_B + Y_A = 0; (2)

Σ M_A(F _i^E) + Σ M_A(R _i^E) = 0 =

= M + P·sin(60⁰)×2 – P·cos(60^о)·1 – R_B×4 = 0. (3)

При составлении выражений (1), (2), (3) использована первая форма уравнений равновесия. Эти уравнения решают в наиболее удобной последовательности и находят проекции неизвестных реакций на координатные оси системы отсчёта OXY или модули этих реакций.

Из уравнения (1) X_A= – Q + P·cos(60^о) = – 4 + 20×0,5 = 6,000 кН.

Из уравнения (3) R_B = (M + P·sin(60^о)×2 – P·cos(60^о)×1)4 =

= (10 + 20×0,866×2 – 20×0,5×1)4 = 8,660 кН.

Из уравнения (2)

Y_A= – R_B + P·sin(60^о) = – 8,66 +20×0,866 = 8,660 кН.

Сила Р разложена на составляющие силы по координатным осям. Это упрощает проецирование силы Р на координатные оси системы отсчёта OXY. Необходимо отметить, что силы раскладываются на составляющие по координатным осям системы отсчёта только в точке их приложения. Порядок решения задачи остается прежним, только использована третья форма уравнений равновесия.

Σ M_С(F _i^E) + Σ M_С(R _i^E) = 0 =

= M – Q·1 – R_B·2 + Y_A·2 – X_A·1 = 0; (4)

Σ M_D(F _i^E) + Σ M_D(R _i^E) = 0 =

= M – Q·1 + P·sin(60^о)·2 – R_B·4 – X_A·1 = 0; (5)

Σ M_Е(F _i^E) + Σ M_Е(R _i^E) = 0 =

= M – P·sin(60⁰)·2 – P·cos(60^о)·1 + Y_A·4 = 0. (6)

Подставляя найденные значения реакций X _A, Y _A, R _B в выражения (4), (5), (6) и вычислив, получим:

Σ M_С(F _i^E) + Σ M_С(R _i^E) = 0 =

= 10 – 4·1 – 8,660·2 + 8,660·2 – 6·1 = 0; (4^I)

Σ M_D(F _i^E) + Σ M_D(R _i^E) = 0 =

= 10 – 4·1 + 20·0,866·2 – 8,660·4 – 6·1 = 0; (5^I)

Σ M_Е(F _i^E) + Σ M_Е(R _i^E) = 0 =

= 10 – 20·0,866·2 – 20·0,5·1 + 8,660·4 = 0. (6^I)

Проведённая проверка подтвердила правильность результатов расчётов. Результаты вычислений помещают в таблицу.

Таблица

Не нашли, что искали? Воспользуйтесь поиском: