Электромеханическая постоянная времени ЭП. Определение жесткости ЭМХ.

Электромеханическая постоянная времени ЭП, характеризует интенсивность протекания переходного процесса. ЭМП ЭП – это время, в течение которого ЭП, обладающий моментом инерции J, разгоняется от неподвижного состояния до угловой скорости идеального холостого хода под действием неизменного момента, равному моменту короткого замыкания (начальному пусковому моменту Мп).

Рассмотрим процесс разгона двигателя постоянного тока при Е_п = const и М=const. Продлим механическую характеристику до пересечения с осью абсцисс (а) и назовем М_кз моментом короткого замыкания: Мкз = с*Iкз, где Iкз=Еп/R.

Кроме того, ω0=Е_п/с.

Жесткость механической характеристики можно выразить несколькими способами:

Уравнение движения привода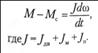

Заменим в уравнении движения приводам М и после преобразований получим

Рассмотрим правую часть этого уравнения: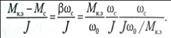

Введем обозначение

Итак, правую часть исходного дифференциального уравнениям но заменить выражением ω_с/Т_м.

Преобразуем второй член:

Таким образом, дифференциальное уравнение для процесса разгона получило вид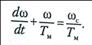

Его решение с учетом начального условия (t=0, ω=0) имеет вид: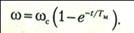

Скорость нарастает по экспоненциальному закону с постоянной времени Тм и стремится к омега с (б)

Электромеханическими характеристиками (ЭМХ) двигателя называются зависимости установившейся частоты вращения от тока – n = f (I) или ω = f (I)

жесткость ЭМХ определяет величину наклона естественной ЭМХ. Величина β зависит от сопротивления якорной цепи и магнитного потока возбуждения.

☻ 33. Передаточная функция ДПТ и регулятора скорости с ПИ-законом регулирования.

Передаточная функция – отношение изображений по Лапласу выходной величины к входной при нулевых начальных условиях. Так, для цепи R – L, подключенной к источнику напряжения u(t) имеем:

или, заменив на р, u(t) на u(p) и i(t) на i(p) и решив уравнение относительно i(p), принятом за выходную величину, получим

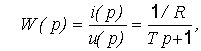
где – постоянная времени.

Для двигателя постоянного тока независимого возбуждения с учетом индуктивности якорной цепи Lя при питании якоря от источника напряжения u(t) и kФ = с, приняв за выходную величину w(t) и за входную u(t) после перехода к изображениям, получим для случая Мс = 0 структурную схему на рис. 5.25,а.

Проделав элементарные преобразования, будем иметь передаточную функцию двигателя в виде колебательного звена (рис. 5.25,б):
,
а)

б) в)
Рис.5.25. Передаточные функции двигателя постоянного тока независимого возбуждения

Реальные ПИ-регуляторы тепловых процессов имеют два вида функциональных схем (рис. 4). В первом варианте (рис. 4, а) сервопривод охватывается отрицательной обратной связью (ООС) и его характеристика не влияет на формирование закона регулирования, целиком определяемого характеристикой устройства обратной связи. Во втором варианте (рис. 4, б) сервопривод не охватывается обратной связью, и ПИ-закон регулирования формируется охватом обратной связью только усилителя К_у. При этом динамические характеристики регулятора в целом определяются динамическими свойствами цепи, состоящей из последовательно включенных замкнутого контура (K_y—W_o.c) и сервопривода. Оба варианта структурных схем ПИ-регуляторов используются в их промышленных исполнениях.

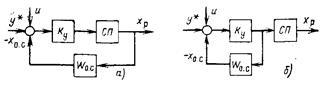
Рис. 4. Структурные схемы ПИ-регуляторов:

а — сервопривод охвачен ООС; б — сервопривод не охвачен ООС

В первом варианте устройство обратной связи должно иметь динамическую характеристику реального дифференцирующего звена

В этом случае регулятор в целом независимо от типа сервопривода воспроизводит динамику ПИ-регулятора

Если принять Т_д=Т_и и K_р=1/K_д, получим

т.е. передаточную функцию ПИ-регулятора, описываемого также дифференциальными уравнениями

и

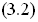
В промышленных ПИ-регуляторах в качестве обратных связей используют различные устройства: электрические, пневматические и гидравлические. Но все они служат аналогами реального дифференцирующего звена, имеют соответствующие ему динамические характеристики, и называются устройствами гибкой или упругой (изменяющейся во времени) обратной связи.

При втором варианте исполнения ПИ-регулятора (рис. 4, б) возможны два случая: 1) сервопривод имеет характеристику интегрального звена (например, электрический или гидравлический сервопривод с переменной скоростью); 2) сервопривод обладает характеристикой пропорционального звена (мембранный сервопривод с уравновешивающей пружиной). В обоих случаях в соответствии с правилом определения результирующей характеристики двух последовательно включенных звеньев

W_p(p) = W_КУУ(p)W_с.п(p), (3.3)

где W_КУУ(p) = 1 ⁄ W_о.с (р).

При использовании сервопривода с передаточной функцией интегрального звена W_с.п(p) = 1⁄ T_Р передаточная функция регулятора имеет вид

При этом для формирования ПИ-закона с помощью устройства обратной связи необходимо, чтобы выдерживалось соотношение

1/W_о.с(р) = W_КУУ(р) = K_р (1+T_Р) (3.5)

что обеспечивает обратная связь с оператором

W_о.с(р) = K_о.с/(1+T_Р) = д/(1+T_Р) (3.6)

Рис. 5. Переходный процесс в устройстве Рис. 6. Переходный процесс ПИ-регулятора обратной связи

Не нашли, что искали? Воспользуйтесь поиском: