Замена переменных в кратном интеграле.

Задание 1

Вычислить двойные интегралы по определению: разбивая область интегрирования D прямыми , (, 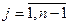) на прямоугольники, составить интегральную сумму

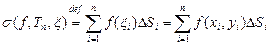
для функции по области , выбирая значения подынтегральной функции в правых вершинах прямоугольников разбиения. Вычислить интеграл, рассматривая его как предел интегральнoй суммы.

№	a	b	c	d	f(x,y)
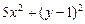
			-1
	-1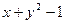
	-2
	-2
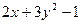
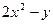
	-1		-2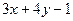
	-1
	-2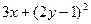
	-1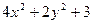
			-1
			-1
	-2		-1
			-1
	-3
	-2	-1

(без общих внутренних точек) множеств, замыкания которых будут элементарными в направлении оси OX или оси OY: . Тогда в силу свойства аддитивности интеграл по множеству D будет равен сумме интегралов по множествам, элементарным в направлении оси OX или OY:

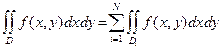
Замечание. Как следует из определения двойного интеграла, если и жорданово множество D симметрично относительно оси

OY, то из чётности функции по переменной x, т.е. из условия , следует, что

.

Из нечётности функции по переменной x, т.е. из условия , следует, что .

Рассмотрим равенство повторных интегралов из правых частей формул (9) и (10):

= .

Оно имеет место для множеств, замыкания которых есть множества, элементарные в направлении осей OX и OY. Переход от левой части этого равенства к правой и наоборот называется изменением порядка интегрирования в повторном интеграле.

Замечания. Обратите внимание на возможные ошибки!

· Пределы интегрирования во внешнем интеграле всегда константы, а пределы интегрирования во внутреннем интеграле, как правило, являются функциями.Пределы интегрирования внешнего и внутреннего интегралов могут быть константами только в том случае, если область интегрирования есть прямоугольник со сторонами, параллельными осям координат.

· В других случаях область интегрирования 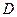разбивают на конечное число элементарных в направлениях осей OX или OY областей в зависимости от вида заданной области. Свойство аддитивности интеграла позволяет вычисление двойного интеграла по области 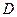свести к вычислению суммы интегралов по каждой из элементарных в направлении какой-либо оси областей.

· Если при некоторых значениях функция, являющаяся нижним пределом в интеграле формулы (9) принимает значение, большее, чем функция, являющаяся верхним пределом то это ошибка. То же относится и к значениям функций в формуле (10). В этом случае следует проверить правильность составления чертежа области интегрирования.

· Ес­ли вместо функций или поставить их значения в конце­вых точках или б, то это ошибка.

· Если множество D симметрично относительно одной из ко­ординатных осей, но не дано условие четности функции f(x, у) относительно соответствующей переменной, то равенство

где часть множества D, лежащая по одну сторону от соответ­ствующей оси, вообще говоря, неверно.

Вопросы для самопроверки

1) Как определяется множество, элементарное в направлении оси OY? оси OX? Какой вид имеет такое множество в плоскости XOY?

2) Как вычислить двойной интеграл по области 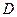, элементарной в направлении оси OY? Оси OX?

3) Как можно разбить область произвольного вида в плоскости XOY на части, каждая из которых будет элементарной в направлении оси OX или OY?

4) Как вычислить двойной интеграл по области произвольного вида в плоскости XOY?

Пример 2. 1)Изменить порядок интегрирования в интеграле .

2) Вычислить , где D - область интегрирования из пункта 1).

Решение.

Y

8

C A (4, 4)

0 4 X

Рис.1

1).a)В заданном повторном интеграле пределы внешнего интеграла по переменной равны 0 и 4. Это означает, что область интегрирования ограничена прямой x = 0 слева и прямой x =4 справа.

Пределы внутреннего интеграла по переменной указывают на то, что область ограничена снизу параболой и сверху прямой . Построив все перечисленные линии, получим область и нтегрирования D(рис1.). Как видно из рисунка, область интегрирования является элементарной в направлении оси ОУ, но не является элементарной в направлении оси ОХ.

b) Для изменения порядка интегрирования область D разбиваем прямой на две области , имеющие общую границу АС. Каждая область будет элементарной в направлении оси ОХ, поэтому заданный интеграл будет равен сумме:

c) Выразим полученные двойные интегралы через повторные по формуле (9). Рассмотрим интеграл по . Как видно из рис.1, наименьшее значение, которое принимает в области , равно 0 в точке(0;0), а наибольшее значение равно 4 в точке (4;4). Следовательно, внешний интеграл по переменной по будет иметь пределы: 0 и 4. Чтобы определить пределы внутреннего интеграла по переменной , проведём мысленно прямую , параллельную оси OX так, чтобы . Тогда при движении слева направо (в направлении возрастания переменной ), эта прямая будет «входить» в область, пересекая прямую , и «выходить» из области, пересекая параболу . Получаем, что - нижний предел. 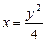Из уравнения параболы получаем - верхний предел. Таким образом, .

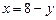d) В области наименьшее и наибольшее значения соответственно равны 4 в точке(4;4) и 8 в точке (0;8). При движении вдоль прямой слева направо, эта прямая «входит» в область, пересекая прямую , и «выходит» из области, пересекая прямую . Получаем, что - нижний предел. Из уравнения получаем - верхний предел. Тогда и общий результат:

= + .

2) По формуле (9) получим

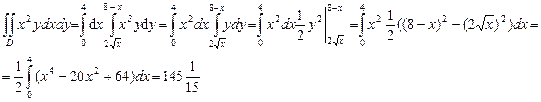
Задание 2

Изменить порядок интегрирования в следующих повторных интегралах:

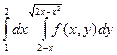
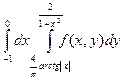
Задание3

Вычислить двойные интегралы по области 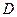, разбивая её при необходимости на области, элементарные в направлении оси OX или OY:

	Двойной интеграл	Уравнения кривых, ограничивающих область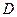
		, ,
		, ,
		, ,
		, ,
		, ,
		,
		, ,
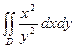
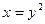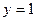
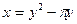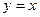
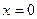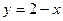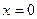		треугольник с вершинами
		, ,
		,
		,
		, , ,
		, , ,
		,

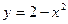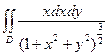
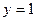
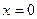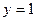
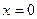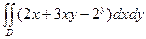
Замена переменных в кратном интеграле.

Зачастую вычисление кратного интеграла приводит к громоздким вычислениям. Это может быть связано либо со способом задания подинтегральной функции, либо с видом области интегрирования. В этом случае упрощение вычислений может быть достигнуто путём перехода к другим координатам - заменой переменной.

Определение 9. Биективное (взаимно однозначное) отображение называется диффеоморфизмом множества D, если и якобиан (определитель J линейного отображения ) не обращается в нуль на D.

Теорема5. Пусть задан диффеоморфизм , множества - жордановы. Пусть далее на жордановом множестве М, задана интегрируемая функция . Тогда композиция интегрируема на множестве M и имеет место формула

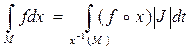
Практически довольно часто возникает необходимость замены переменных при помощи отображения, которое не является диффеоморфизмом на всей области D _t. В этом случае может быть применена следующая теорема.

Теорема 6. Пусть , x=x(t) –отображение жорданова множества 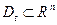в жорданово множество . Если существуют множества меры нуль и , такие, что множества \ и \ - открытые, отображение х: \ \ - диффеоморфизм, и якобиан J отображения x определен и ограничен на D_t, то для любой функции функция 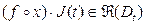и имеет место формула

(11)

Отметим, что в теореме о замене переменных в кратном интеграле утверждается не только равенство исходного и преобразованного интегралов, но и существование преобразованного интеграла, в частности то, что множество изменения новых переменных жорданово. На практике часто существование обоих интегралов устанавливается непосредственно и вопрос идет только об их равенстве.

Не нашли, что искали? Воспользуйтесь поиском: