Замена переменных в двойном интеграле.

Пусть двойной интеграл преобразуется от декартовых координат , , , 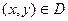- жорданово, к криволинейным координатам 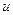, , связанным с декартовыми координатами соотношениями

,

где функции и имеют непрерывные частные производные на жордановом множестве 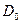плоскости и якобиан преобразования в 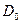не обращается в 0:

.

Формула замены переменной (11) в этом случае имеет вид:

. (12)

При этом выбор функций определяется теми соотношениями, которые задают область интегрирования. Как правило, стремятся подобрать эти функции так, чтобы упростить в новых координатах область интегрирования, а следовательно, и вычисления.

Замечание. Если связь переменных и задаётся соотношениями , и нахождение явных выражений затруднено, для вычисления якобиана 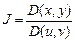можно воспользоваться равенством 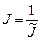, где 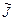есть якобиан обратного отображения , т.е. .

Пример 3. Вычислить двойной интеграл , D – область, ограниченная четырьмя параболами , , , , , .

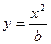Решение. Построим область D (рис. 2). Исходя из уравнений парабол, ограничивающих D, , введем новые переменные по формулам . Тогда: или .

Рис.2

Вычислим якобиан .

Область изменения новых переменных- прямоугольник. Обозначим его . Получим:

Преобразование двойного интеграла от прямоугольных координат , к полярным и , связанным с прямоугольными координатами соотношениями

,

,

осуществляется по формуле

,

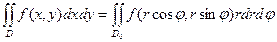где 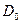- прообраз D, - полярный радиус, , , - полярный угол, изменяющийся в промежутке длиной не более :

.

Для упрощения записи в дальнейшем не будем вводить новое обозначение для множества изме­нения rи , а будем рассматривать множество D как в виде D= ={(х, у):...}, так и в виде D={(r, ):...}, где вместо многоточия стоят условия на координаты (х, у) и (r, ) соответственно. Это связано с тем, что переход от переменных х и у к переменным r и можно рассматривать не как преобразование мно­жества D, а как переход к согласованной с декарто­вой полярной системе координат. Нахождение прообраза множества D при переходе к полярным координатам на плоскости, т.е. при отображении, , облегчается геометрическим смыслом параме­тров r и . Длина радиус-вектора из начала коор­динат в точку (х, у) есть r, а — угол между этим вектором и положи­тельным направлением оси ОХ.

Обобщенными полярными координатами называется пара (r, ), связанная с координатами (х, у) формулами

либо

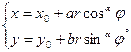
При этом предполагается, что 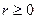, - постоянная, а пробегает промежуток 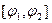, который выбирается в зависимости от значения постоянной так, чтобы функции 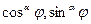имели смысл и оба равенства

одновремен­но выполнялись только в концевых точках этого промежутка.

Переход к обобщенным полярным координатам делается в основном тогда, когда уравнение кривой, которая ограничивает область интегрирования D, в новых переменных при соответствующем выборе постоянных становится существенно более простым. Так как обобщенные полярные координаты не имеют наглядного геометрического смысла, то границы их изменения для точек (х, у) из данного множества D определяются аналитиче­ским путем. Если при переходе к полярным координатам мы оставляли обозначение множества D без изменения, то теперь, как и в общем случае замены переменных, будем соответствую­щее множество значений (r, ) обозначать через . 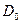Якобиан при переходе к обобщенным полярным координатам равен

.

Замечания.

· В том случае, когда при переходе к обобщённым полярным координатам значение постоянной 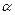меньше 1, нарушаюся условия биективности и гладкости отображения, осуществляющего эту замену переменных. В этом случае при замене переменной может появиться несобственный двойной интеграл по ограниченному жорданову множеству от неограниченной функции. Аналогичная ситуация может возникнуть и в случае замены переменных посредством криволинейных координат. Оба одномерных интеграла в повторном могут быть несобственными. Вопрос об их существовании решается одновременно с их вычислением. Формула замены переменной остаётся верной, важно лишь, чтобы условие гладкости отображения, осуществляющего эту замену, нарушалось только на множестве меры нуль.

· При вычислении повторных интегралов множители, не зависящие от переменной интегрирования, можно выносить за знак соответствующего интеграла по этой переменной.

Пример 5.

Вопросы для самопроверки

По какой формуле вычисляется двойной интеграл в случае замены переменных посредством перехода от декартовых координат

1) к криволинейным?

2) к полярным координатам?

3) к обобщённым полярным координатам?

Задание 4

В двойном интеграле в зависимости от вида заданной области перейти к полярным или обобщённым полярным координатам, расставить в новых координатах пределы интегрирования. В декартовых координатах область интегрирования задаётся следующими соотношениями:

,

где – множества точек, удовлетворяющих условиям:

			,
	, , ,		,
	,		,
	,
	,		, ,
	, ,		,
	,		,
	, ,		,
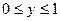
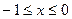
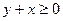
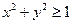			квадрат с вершинами , , ,

Задание 5

Вычислить интеграл , переходя к полярным (или обобщённым полярным) координатам, если функция и область интегрирования 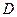задаются условиями:

		,
		,
		, ,
		,
		,
		,
		,
		,
		, ,

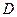
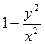
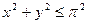
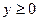
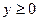
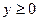
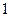
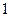
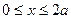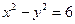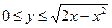
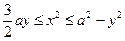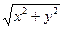
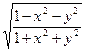
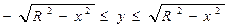
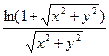
Задание 6. С помощью подходящей замены переменных , вычислить интеграл , где функция и область интегрирования 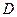заданы в таблице:

Не нашли, что искали? Воспользуйтесь поиском: