Вычисление тройного интеграла

Для вычисления тройного интеграла с помощью теоремы Фубини обычно пространство представляют в виде декартова произведения двух пространств меньшей размерности двумя способами: или . Рассмотрим, например, представления и (остальные варианты представлений получаются из этих двух перестановкой обозначений осей координат). Сформулируем теорему Фубини для представления [1].

Теорема 7. Пусть 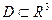- жорданово множество, элементарное в направлении оси OZ, т. е.: ,

. Если , то:

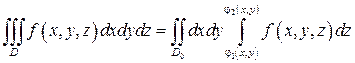. (14)

В случае представления пространства 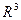в виде декартова произведения теорема Фубини формулируется следующим образом:

Теорема 8. Пусть – область в 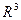, ограниченная кусочно-гладкой замкнутой поверхностью без самопересечений, и . Тогда тройной интеграл по области D вычисляется по формуле:

, (15)

где промежуток есть ортогональная проекция на ось OX, множество есть пересечение с плоскостью (сечение вертикальной плоскостью ).

При данных условиях множества ограничены кусочно-гладкими замкнутыми кривыми без самопересечений (связность не обязательна), следовательно, являются жордановыми множествами так же, как и область (св-во 7 жордановых множеств §1). Интеграл представляет интегрируемую функцию на , следовательно, все интегралы, входящие в равенство, имеют смысл.

Если в области D 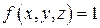, то

,

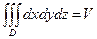где V – объем области D.

Механический смысл тройного интеграла. В случае, когда подынтегральная функция 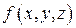задает плотность тела, занимающего область D, тройной интеграл выражает массу этого тела:

,

где через обозначен элемент объема.

Рассмотрим возможность вычисления тройного интеграла через повторные.

Область 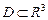будем элементарной, если прямые, параллельные осям координат, пересекают замыкание области D не более чем в двух точках. В декартовой системе координат область D удобно разбивать на элементарные плоскостями, параллельными координатным плоскостям. В частности, если элементарная область имеет вид:

, , ,

то

. (16)

При этом предполагается, что функции, определяющие границы интегрирования одномерных интегралов, являются гладкими.

Представление тройного интеграла в виде последовательности трёх одномерных, как,в частности, в правой части формулы (16) называют расстановкой пределов в тройном интеграле.

B правой части формулы (16) сначала интегрируют функцию 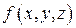по одной переменной z, полагая, что оставшиеся две переменные принимают любые постоянные значения в области интегрирования. Затем результат интегрируют по второй переменной у, при любом постоянном значении третьей переменной в D и, наконец, выполняют интегрирование по третьей переменной х в максимальном диапазоне ее изменения в D.Порядок, в котором следуют переменные интегрирования в повторном интеграле формулы (16) определяется видом области интегрирования.

Как и в случае двойного интеграла, обычно область интегрирования разбивают на простые области таким образом, чтобы вычисление полученных повторных интегралов было наименее сложным.

Замечание. Представление пространства в виде декартовых произведений способами: или позволяет свести решение задачи перестановки порядка интегрирования в тройном интеграле к перестановке порядка интегрирования в двойном интеграле, меняя местами либо первые две, либо последние две из трёх координат.

Пример 8.

Задание 9.

Расставить пределы интегрирования всеми возможными способами и вычислить объём тела , ограниченного указанными поверхностями.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

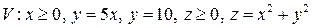16. .

17. .

18. .

19. .

20. .

21. .

22. .

23. .

24. .

25. .

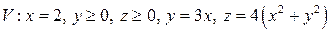26. .

27. .

28. .

29. .

30. .

Не нашли, что искали? Воспользуйтесь поиском: