
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Поверхностные интегралы
Определение12. Множество 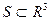 называется поверхностью в
называется поверхностью в 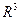 , если для любой точки
, если для любой точки 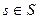 существует открытая окрестность, гомеоморфная замкнутому кругу в
существует открытая окрестность, гомеоморфная замкнутому кругу в 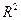 .
.
Напомним, что гомеоморфизм - биективное отображение, непрерывное вместе с обратным к нему.
1. Определение 13. Поверхность S называется простой гладкой поверхностью, если 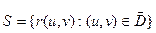 , где отображение r:
, где отображение r:  - гомеоморфизм жордановой области D;
- гомеоморфизм жордановой области D; 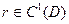 ;
;
2. для всех точек 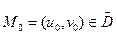 ранг матрицы
ранг матрицы
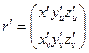
равен двум в точке 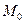 , т.е. в точках
, т.е. в точках 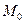 векторы
векторы 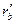 и
и  неколлинеарны.
неколлинеарны.
Отображение 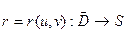 называется параметрическим представлением поверхности S; переменные и и v — параметрами S; жорданово множество D — областью значения параметров и, v. Точки
называется параметрическим представлением поверхности S; переменные и и v — параметрами S; жорданово множество D — областью значения параметров и, v. Точки 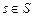 , будем называть внутренними, если они являются образами точек D. Точки
, будем называть внутренними, если они являются образами точек D. Точки 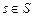 , являющиеся образами границы
, являющиеся образами границы 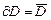 \
\ 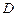 ,, будем называть граничными точками S.
,, будем называть граничными точками S.
Определение 14. Поверхность S называется кусочно-гладкой, если она может быть представлена в виде объединения конечного числа простых гладких поверхностей, попарно пересекающихся, возможно, лишь их замыканиям, представляющим собой кусочно-гладкие кривые без самопересечений.
Пусть 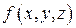 – определённая и непрерывная функция в точках некоторой гладкой поверхности
– определённая и непрерывная функция в точках некоторой гладкой поверхности 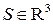 . С помощью кусочно-гладких кривых, принадлежащих поверхности S, произведём разбиение этой поверхности на n элементарных площадок
. С помощью кусочно-гладких кривых, принадлежащих поверхности S, произведём разбиение этой поверхности на n элементарных площадок 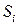 , площади которых обозначим
, площади которых обозначим 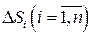 , а диаметры –
, а диаметры – 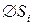 . На каждой площадке разбиения
. На каждой площадке разбиения 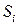 , выберем произвольную точку
, выберем произвольную точку 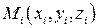 , вычислим
, вычислим 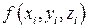 и составим интегральную сумму
и составим интегральную сумму
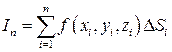 .
.
Определение 15. Предел последовательности интегральных сумм  при стремлении даметра разбиения к 0
при стремлении даметра разбиения к 0 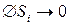 , называется поверхностным интегралом первого рода от функции
, называется поверхностным интегралом первого рода от функции 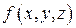 по поверхности S и обозначается
по поверхности S и обозначается
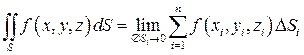 .
.
Определение поверхностного интеграла первого рода переносит определение двойного интеграла Римана от непрерывной функции по плоской области, лежащей в 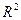 , на гладкую поверхность S, лежащую в
, на гладкую поверхность S, лежащую в 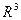 . Существование данного в определении 15 интеграла обеспечивается критерием Лебега.
. Существование данного в определении 15 интеграла обеспечивается критерием Лебега.
Поверхностные интегралы первого рода обладают свойствами линейности, аддитивности, для них справедлива теорема о среднем, их величина не зависит от выбора стороны поверхности.
Геометрический смысл поверхностного интеграла. Если  , то интеграл
, то интеграл 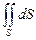 равен площади поверхности
равен площади поверхности  :
: 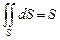 .
.
Замечания.1). Величина площади поверхности определяется внутренней геометрией поверхности и не зависит от способа представления поверхности. Следовательно, величина площади поверхности не зависит от способа параметризации поверхности.
2). Площадь простой кусочно-гладкой поверхности определяется и вычисляется как сумма площадей простых гладких поверхностей, составляющих её.
3). Аналогично определяется и площадь простой гладкой поверхности, если она задаётся гомеоморфизмом, у которого условия гладкости не выполняются на множестве площади 0.
Механический смысл поверхностного интеграла состоит в том, что если функция 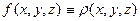 – выражает поверхностную плотность поверхности S, то интеграл
– выражает поверхностную плотность поверхности S, то интеграл 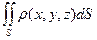 равен массе поверхности S:
равен массе поверхности S:
 .
.
Если всякая прямая, параллельная, например, оси OZ, пересекает поверхность S лишь в одной точке, будем говорить, что проекция D поверхности S на плоскость OXY однозначна.
Пусть 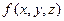 – непрерывная функция,
– непрерывная функция, 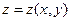 – гладкая поверхность
– гладкая поверхность  , где
, где 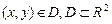 . Если проекция
. Если проекция 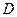 поверхности
поверхности  на плоскость XOY однозначна, то соответствующий поверхностный интеграл 1 рода вычисляется по формуле
на плоскость XOY однозначна, то соответствующий поверхностный интеграл 1 рода вычисляется по формуле
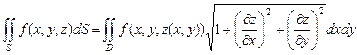 , (28)
, (28)
где  – элемент площади поверхности, т.е.
– элемент площади поверхности, т.е.
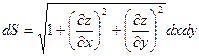 . (29)
. (29)
Пусть в области  плоскости XOY задана непрерывная функция
плоскости XOY задана непрерывная функция 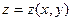 , имеющая непрерывные частные производные. Поверхность, определяемая такой функцией, будет гладкой. Обозначим
, имеющая непрерывные частные производные. Поверхность, определяемая такой функцией, будет гладкой. Обозначим  -область, являющуюся проекцией рассматриваемой поверхности на плоскость XOY. Площадь
-область, являющуюся проекцией рассматриваемой поверхности на плоскость XOY. Площадь 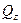 поверхности
поверхности 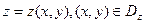 , вычисляется по формуле
, вычисляется по формуле

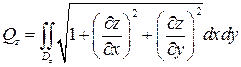 . (30)
. (30)
В случае, когда гладкая поверхность задана функцией 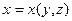 на жордановом множестве
на жордановом множестве  (или функцией
(или функцией 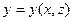 на жордановом множестве
на жордановом множестве 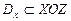 ), площадь такой поверхности вычисляется по аналогичной формуле, в которой под знаком радикала стоят частные
), площадь такой поверхности вычисляется по аналогичной формуле, в которой под знаком радикала стоят частные
Пример 16. Вычислить поверхностный интеграл первого рода
 , где W - поверхность цилиндра
, где W - поверхность цилиндра 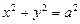 , заключённая между плоскостями z = 0 и z = h.
, заключённая между плоскостями z = 0 и z = h.
Решение. Здесь для всей поверхности W нельзя выразить одну из координат однозначной функцией от других координат. Части цилиндрической поверхности, расположенные по разные стороны от вертикальных координатных плоскостей (рис.6), имеют различные
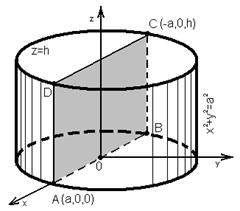
Рис.6
явные уравнения: часть 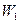 , расположенная слева от плоскости xOz,
, расположенная слева от плоскости xOz,
имеет уравнение 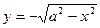 , а часть
, а часть  , расположенная справа от
, расположенная справа от
этой плоскости, имеет уравнение 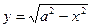 .Поэтому вычисляем
.Поэтому вычисляем
данный интеграл К по поверхности W как сумму интегралов 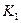 и
и 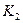 по составляющим её частям
по составляющим её частям 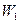 и
и  .Преобразуя поверхностные интегралы
.Преобразуя поверхностные интегралы 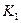 и
и 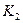 в двойные интегралы с переменными x и z, получим:
в двойные интегралы с переменными x и z, получим:
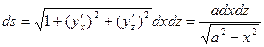 ,
, 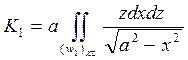 ,
,  .
.
Следовательно,
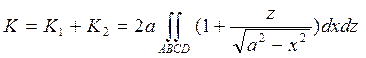 ,
,
так как прямоугольник ABCD есть общая проекция поверхностей 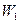 и
и  на плоскость xOz.
на плоскость xOz.
Вычисляя полученный двойной интеграл, найдём:
Вопросы для самопроверки
По какой формуле можно вычислить площадь простой гладкой поверхности  , заданной уравнением
, заданной уравнением 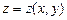 ,
,  ?
? 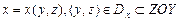 ?
? 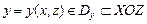 ? Какова формула вычисления поверхностного интеграла первого рода по такой поверхности от функции
? Какова формула вычисления поверхностного интеграла первого рода по такой поверхности от функции  ,
, 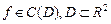 ?
?
Задание 14
Вычислить поверхностные интегралы первого рода
| № | Интеграл | Область S |
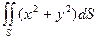
| часть поверхности 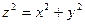 (конус) между плоскостями (конус) между плоскостями  и и 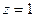
| |

| часть плоскости  , заключенная в первом октанте , заключенная в первом октанте
| |
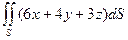
| часть плоскости  , расположенная в первом октанте , расположенная в первом октанте
| |
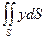
| полусфера 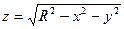
| |
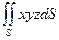
| часть плоскости  , расположенная в первом октанте , расположенная в первом октанте
| |
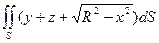
| поверхность цилиндра 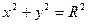 , заключенная между плоскостями , заключенная между плоскостями  и и 
| |
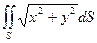
| боковая поверхность конуса  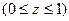
| |
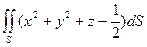
| конечная часть поверхности 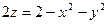 , отсеченная плоскостью , отсеченная плоскостью 
| |
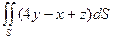
| часть плоскости 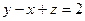 , расположенная во втором октанте , расположенная во втором октанте
| |
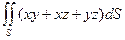
| часть поверхности конуса 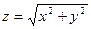 , отсекаемая цилиндром , отсекаемая цилиндром 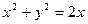
| |
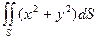
| поверхность, отсекаемая от параболоида 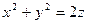 плоскостью плоскостью 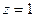
| |
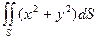
| поверхность конуса 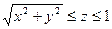
| |
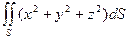
| поверхность куба 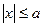 , ,  , , 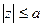
| |
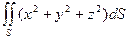
| полная поверхность цилиндра 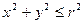 , , 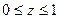
| |

| часть плоскости  , расположенная в первом октанте , расположенная в первом октанте
| |
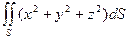
| поверхность октаэдра 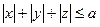
| |
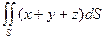
| поверхность тела, ограниченного плоскостью  , полусферой , полусферой 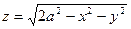 и конусом и конусом 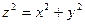 , , 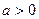
| |

| часть цилиндра  , лежащая между конусом , лежащая между конусом 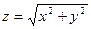 и параболоидом и параболоидом 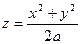
| |
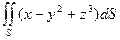
| часть цилиндра 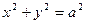 , ,  , лежащая между плоскостями , лежащая между плоскостями 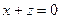 , , 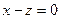
| |
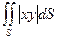
| поверхность тела, образованного пересечением цилиндров 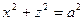 , , 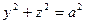
|
Поверхностные интегралы второго рода рассматриваются только по ориетированным поверхностям.
Напомним, что такое ориентация кусочно-гладкой поверхности в 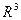 . Пусть
. Пусть  — простая гладкая поверхность, т. е.
— простая гладкая поверхность, т. е.
 ,
,
где область  жорданова, гомеоморфизм
жорданова, гомеоморфизм
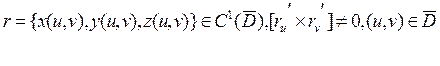 .
.
В каждой точке гладкой поверхности можно построить вектор нормали 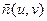 . Тем самым вводится вектор-функция
. Тем самым вводится вектор-функция 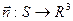 , которую называют векторным полем нормальных векторов к S. Тогда векторное поле
, которую называют векторным полем нормальных векторов к S. Тогда векторное поле 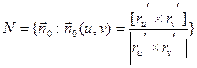 будет непрерывным полем единичных нормальных векторов к S.
будет непрерывным полем единичных нормальных векторов к S.
Определение 16. Гладкая (т. е. имеющая в каждой точке касательную плоскость) поверхность 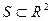 называется ориентируемой или двусторонней, если на ней можно задать непрерывное поле единичных нормальных векторов. Такое поле называют ориентирующим полем нормалей S.
называется ориентируемой или двусторонней, если на ней можно задать непрерывное поле единичных нормальных векторов. Такое поле называют ориентирующим полем нормалей S.
Как следует из вышесказанного, простая гладкая поверхность ориентируема. [1,с.222]
Определение 17. Ориентированной поверхностью называется ориентируемая поверхность с выбранным ориентирующим полем нормалей. Можно сказать, что выбор направления нормали определяет сторону поверхности. Поэтому ориентацию поверхности часто называют выбором стороны поверхности — отсюда термин «двусторонняя поверхность». Двухсторонние поверхности характеризуются следующим свойством: если основание вектора нормали 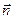 непрерывно перемещать по любому замкнутому контуру L, лежащему на такой поверхности, то при возвращении в исходную точку направление
непрерывно перемещать по любому замкнутому контуру L, лежащему на такой поверхности, то при возвращении в исходную точку направление 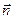 совпадет с исходным. Примерами двухсторонних поверхностей являются плоскости, все поверхности второго порядка, тор и многие другие.
совпадет с исходным. Примерами двухсторонних поверхностей являются плоскости, все поверхности второго порядка, тор и многие другие.
Сторону гладкой поверхности S, из каждой точки которой восставлен вектор нормали n, будем называть положительной, а другую ее сторону (если она существует) – отрицательной. Если, в частности, поверхность S является замкнутой и ограничивает некоторое жорданово множество D, то положительной или внешней стороной поверхности называют ту ее сторону, нормальные векторы к которой направлены от множества D, а отрицательной или внутренней – сторона, нормальные векторы которой направлены в множество D. Например, на сфере можно задать непрерывное поле внешних — направленных от центра — нормальных векторов или сказать, что задана внешняя сторона сферы; если же задать поле внутренних — направленных к центру— нормальных векторов, то можно сказать, что задана внутренняя сторона сферы.
Если же на поверхности найдётся замкнутый контур, при непрерывном перемещении вдоль которого вектор нормали, возвращаясь в исходную точку, изменяет своё первоначальное направление на противоположное, то такую поверхность называют односторонней. Для односторонних поверхностей указанное перемещение нормали 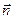 при возвращении в исходную точку приводит к «антинормали», т.е. к вектору
при возвращении в исходную точку приводит к «антинормали», т.е. к вектору 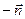 . Классическим примером односторонней поверхности является лист Мёбиуса.
. Классическим примером односторонней поверхности является лист Мёбиуса.
Если поверхность S задана уравнением 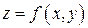 , то нормальный вектор
, то нормальный вектор 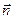 , образующий с положительным направлением оси OZ острый угол
, образующий с положительным направлением оси OZ острый угол 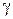 , определяется следующим образом:
, определяется следующим образом:
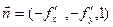 ,
,
а координаты единичного вектора нормали  равныего направляющим косинусам, т.е.
равныего направляющим косинусам, т.е.
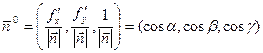 ,
, 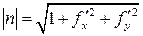 .
.
Если поверхность S задана уравнением 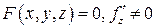 , то
, то
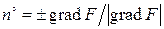 ,
,
где знак «+» берется в случае, когда угол 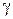 – острый, а знак «–» в случае, когда
– острый, а знак «–» в случае, когда 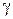 – тупой [2].
– тупой [2].
Пусть в области 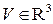 определена векторная функция
определена векторная функция  , где
, где 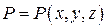 ,
, 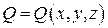 ,
, 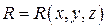 – функции, непрерывные на жордановом множестве V. Далее, пусть S – некоторая гладкая поверхность, принадлежащая V,
– функции, непрерывные на жордановом множестве V. Далее, пусть S – некоторая гладкая поверхность, принадлежащая V, 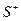 – сторона гладкой поверхности
– сторона гладкой поверхности  , характеризуемая направлением нормали
, характеризуемая направлением нормали 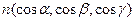 . Тогда поверхностный интеграл 2 рода выражается формулой:
. Тогда поверхностный интеграл 2 рода выражается формулой:
 (31)
(31)
Таким образом, по определению
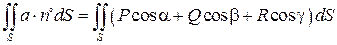 ,
,
т.е. поверхностный интеграл 2-го рода есть поверхностный интеграл 1-го рода от скалярного произведения вектор-функции на единичный вектор нормали к выбранной стороне повеохности.
Поверхностные интегралы второго рода обладают свойствами линейности и аддитивности. При изменении стороны поверхности на противоположную, т.е. при замене 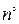 на –
на – 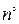 , интеграл (31) изменяет знак.
, интеграл (31) изменяет знак.
Так как
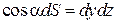 ,
, 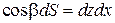 ,
, 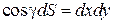 ,
,
то интеграл (31) можно записать и в виде
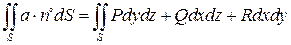 . (32)
. (32)
Если поверхность S задается функцией 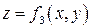 ,
, 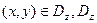 - жорданово множество в
- жорданово множество в 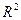 , то справедлива следующая формула, сводящая вычисление интеграла (31) к вычислению двойного интеграла:
, то справедлива следующая формула, сводящая вычисление интеграла (31) к вычислению двойного интеграла:
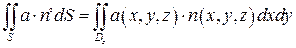 , (33)
, (33)
где область  является проекцией поверхности S на плоскость XOY
является проекцией поверхности S на плоскость XOY
 .
.
При вычислении двойного интеграла, стоящего в правой части формулы (28) переменную z следует заменить на 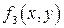 .
.
Приведем еще две формулы, которые можно применять для вычисления поверхностного интеграла второго рода:
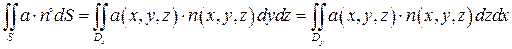 , (34)
, (34)
где области 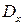 и
и 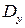 – соответственно проекции поверхности S на плоскости OZY и OXZ; поверхность S задается соответственно функциями
– соответственно проекции поверхности S на плоскости OZY и OXZ; поверхность S задается соответственно функциями 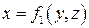 и
и 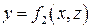 . В двойном интеграле по области
. В двойном интеграле по области 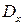 следует в подынтегральном выражении заменить х функцией
следует в подынтегральном выражении заменить х функцией 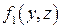 , и принять
, и принять
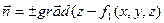 ,
,
а в двойном интеграле по 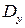 – заменить функцией
– заменить функцией 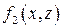 и положить
и положить
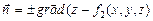 .
.
Отметим, что в выражениях для n знак «+» или «–» выбирается в зависимости от того, острый или тупой угол 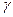 .
.
1) Какова формула вычисления поверхностного интеграла второго рода по выбранной стороне двусторонней поверхности  ?
?
2) Какой тип поверхностных интегралов зависит от выбора стороны поверхности  ? От чего зависит знак перед интегралом по выбираемой стороне поверхности?
? От чего зависит знак перед интегралом по выбираемой стороне поверхности?
Пример 17.
Задание 15
Вычислить поверхностные интегралы второго рода через полную поверхность тетраэдра  , образованного плоскостью
, образованного плоскостью 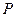 и координатными плоскостями в направлении внешней нормали к его поверхности:
и координатными плоскостями в направлении внешней нормали к его поверхности:
| № | Вычислить интеграл | Плоскость 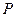
|

| 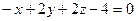
| |
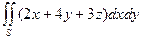
| 
| |
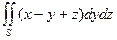
| 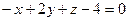
| |
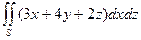
| 
| |

| 
| |

| 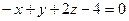
| |

| 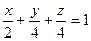
| |
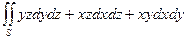
| 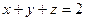
| |
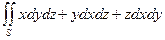
| 
| |
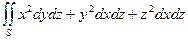
| где  – внешняя сторона полной поверхности конуса – внешняя сторона полной поверхности конуса  , , 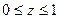
| |
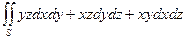
| где  – внешняя сторона поверхности в первом октанте, образованной цилиндром – внешняя сторона поверхности в первом октанте, образованной цилиндром 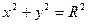 и плоскостями и плоскостями 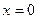 , ,  , ,  , , 
| |
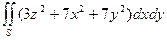
| где  – внутренняя сторона полусферы – внутренняя сторона полусферы 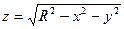 , вырезанной конусом , вырезанной конусом 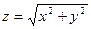
| |

| где  – верхняя сторона поверхности – верхняя сторона поверхности 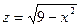 , отсеченной плоскостями , отсеченной плоскостями  , , 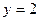
| |
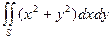
| где  – внутренняя сторона части поверхности – внутренняя сторона части поверхности  , отсеченной плоскостью , отсеченной плоскостью 
| |
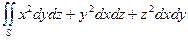
| где  – внешняя сторона поверхности куба – внешняя сторона поверхности куба  , , 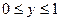 , , 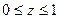
| |
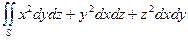
| где  – внешняя сторона части сферы – внешняя сторона части сферы 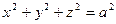 в первом октанте в первом октанте
|
Формулы Стокса и Остроградского-Гаусса
Если функции  ,
, 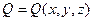 ,
,  непрерывны вместе со своими частными производными первого порядка в замыкании жорданова множества
непрерывны вместе со своими частными производными первого порядка в замыкании жорданова множества 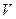 пространства
пространства 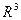 , а
, а  – внешняя сторона кусочно-гладкой замкнутой поверхности, ограничивающей это множество, то справедлива формула Остроградского-Гаусса:
– внешняя сторона кусочно-гладкой замкнутой поверхности, ограничивающей это множество, то справедлива формула Остроградского-Гаусса:
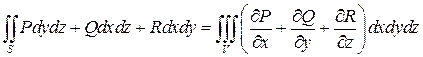 (35)
(35)
или в другом виде
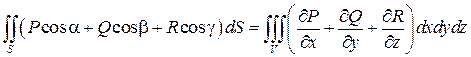 ,
,
где 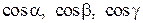 – направляющие косинусы внешней нормали к поверхности S.
– направляющие косинусы внешней нормали к поверхности S.
Если контур L лежит на поверхности S, то назовем часть S, ограниченную L, поверхностью, натянутой на контур L. Если поверхность S ориентируема и контур L ориентирован, то ориентацию S, при которой заданный обход контура L положителен, назовем согласованной с ориентацией L.
' Теорема (формула Стокса). Пусть область 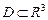 ; функции Р, Q, R
; функции Р, Q, R 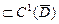 ;
; 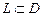 - ориентированный контур и
- ориентированный контур и 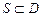 S — натянутая на L ориентированная поверхность, ориентация которой согласована с ориентацией L. Тогда
S — натянутая на L ориентированная поверхность, ориентация которой согласована с ориентацией L. Тогда
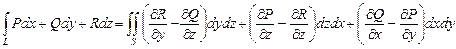 (36)
(36)
На практике поверхностный интеграл второго рода, стоящий справа, часто переводят в поверхностный интеграл, первого рода и пользуются формулой Стокса в виде
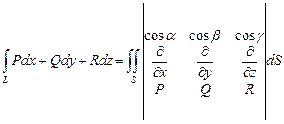 ,
,
где 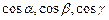 — направляющие косинусы вектора нормали к S, характеризующего ориентацию S.
— направляющие косинусы вектора нормали к S, характеризующего ориентацию S.
Замечание. Естественная область применения формул Грина и Остроградского- Гаусса — это интегралы второго рода по замкнутым контурам на плоскости и замкнутым поверхностям в пространстве. Но иногда, особенно в пространстве, вычисления упрощаются, если замкнуть незамкнутую поверхность или кривую и считать данный интеграл как разность преобразованного интеграла по замкнутой поверхности или кривой и соответствующего интеграла по замыкающему множеству. В качестве такого множества обычно берутся отрезки прямых или части плоскостей, параллельных координатным, поскольку по таким множествам интеграл второго рода вычисляется наиболее просто.
Пример 18. По формуле Остроградского – Гаусса вычислить поверхностный интеграл 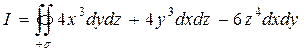 ,
,
где σ – полная поверхность цилиндра 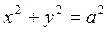 (см. рис.6).
(см. рис.6).
Решение. Путём сопоставления данного интеграла с левой частью формулы (35), определяем: P = 4x ³, Q = 4y³,  . Затем находим производные:
. Затем находим производные:  ,
, 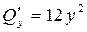 ,
,  , подставляем их в правую часть формулы (35) и таким образом вместо данного поверхностного интеграла по замкнутой поверхности σ получим тройной интеграл по области G, ограниченной поверхностью:
, подставляем их в правую часть формулы (35) и таким образом вместо данного поверхностного интеграла по замкнутой поверхности σ получим тройной интеграл по области G, ограниченной поверхностью:
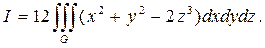
Интегрируя cначала по z, затем перейдём к полярным координатам:
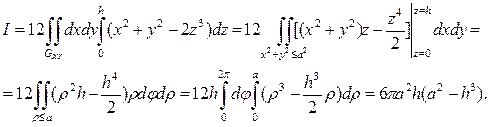
Пример 19. Вычислить криволинейный интеграл  , пользуясь формулой Стокса,
, пользуясь формулой Стокса,
где L – замкнутая линия OCBAO (рис.7) пересечения поверхностей 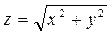 , х = 0, х = 2, у = 0, у = 1.
, х = 0, х = 2, у = 0, у = 1.
Решение.
Сопоставляя К с Формулой (36), определяем:
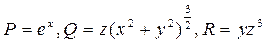 .
.
Находим производные:
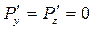 ,
, 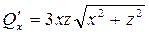 ,
,  ,
, 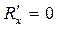 ,
, 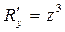 .
.
Подставляя их в формулу Стокса, получим
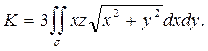
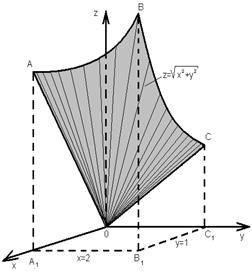 Здесь σ может быть любая (гладкая или кусочно-гладкая) поверхность, «натянутая» на данный контур L. Пользуясь этим, выберем в качестве σ часть данной
Здесь σ может быть любая (гладкая или кусочно-гладкая) поверхность, «натянутая» на данный контур L. Пользуясь этим, выберем в качестве σ часть данной
конической поверхности 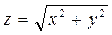 ,
,
ограниченную контуром L. Тогда,
интегрируя по нижней стороне
указанной поверхности, на которой
заданный обход контура L на-
правлен против часовой стрелки, найдём:

( - прямоугольник
- прямоугольник 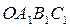 ). Рис.7
). Рис.7
Задание 16
Применяя формулу Стокса, вычислить интегралы по контуру 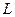 .
.
| № | Вычислить интеграл | Контур 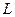
| Ориентация 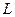 положительна относительно вектора положительна относительно вектора
|
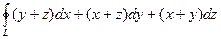
| 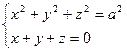
| 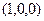
| |
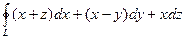
| 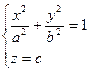
| 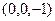
| |
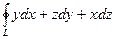
| 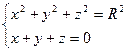
| 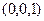
| |

| 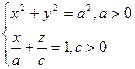
| 
| |
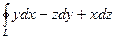
| 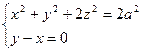
| 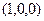
| |
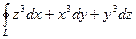
| 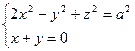
| 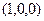
| |


| 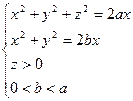
| 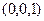
| |
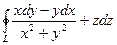
| 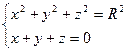
| 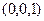
|
С помощью формулы Остроградского-Гаусса вычислить интегралы:
| № | Вычислить интеграл | 
|

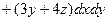
|  – внешняя сторона поверхности пирамиды – внешняя сторона поверхности пирамиды 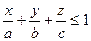 , ,  , , 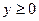 , , 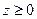
| |
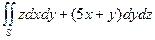
|  – внешняя сторона полной поверхности конуса – внешняя сторона полной поверхности конуса 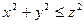 , , 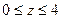
| |
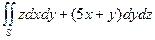
|  – внутренняя сторона эллипсоида – внутренняя сторона эллипсоида 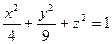
| |
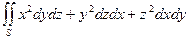
|  – внутренняя сторона поверхности параллелепипеда – внутренняя сторона поверхности параллелепипеда 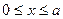 , ,  , , 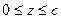
| |
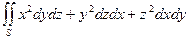
|  – внешняя сторона полной поверхности – внешняя сторона полной поверхности  , , 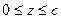 (конус) (конус)
| |
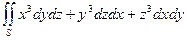
|  – внутренняя сторона сферы – внутренняя сторона сферы 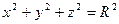
| |
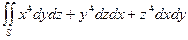
|  – сфера – сфера 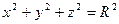
| |
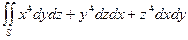
|  – внешняя сторона полной поверхности полушара – внешняя сторона полной поверхности полушара 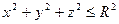 , , 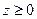
|
Элементы векторного анализа
Пусть 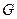 – жорданово множество в трехмерном пространстве. Скалярным полем на
– жорданово множество в трехмерном пространстве. Скалярным полем на  называют числовую функцию
называют числовую функцию 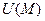 , заданную в точках
, заданную в точках 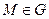 . Векторным полем на
. Векторным полем на 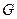 называют векторную функцию a (M), заданную в точках
называют векторную функцию a (M), заданную в точках 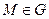 :
:
a (M)= P(x,y,z) i+ Q(x,y,z) j +R(x,y,z) k, M=(x,y,z).
В заданной системе декартовых координат обе функции становятся функциями координат точек 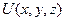 , a
, a 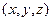 .
.
Определение 17. Градиентом дифференцируемого на 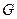 скалярного поля в точке
скалярного поля в точке 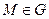 называют вектор, обозначаемый grad Uи задаваемый формулой
называют вектор, обозначаемый grad Uи задаваемый формулой
grad 
где производные поля 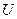 вычислены в точке
вычислены в точке 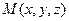 . Значение
. Значение
grad 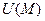 не зависит от выбора декартовой системы координат, т.е. вектор-функция grad U является векторным полем на
не зависит от выбора декартовой системы координат, т.е. вектор-функция grad U является векторным полем на 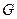 .
.
Физический смысл градиента. Вектор 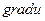 к каждой точке
к каждой точке 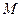 скалярного поля
скалярного поля 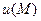 ортогонален поверхности уровня этого поля и указывает направление наиболее быстрого роста функции
ортогонален поверхности уровня этого поля и указывает направление наиболее быстрого роста функции 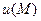 , а его величина
, а его величина 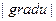 дает скорость этого роста.
дает скорость этого роста.
Определение 18. Дивергенцией или расходимостью дифференцируемого на 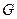 векторного поля
векторного поля 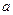 в точке
в точке 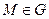 называют число, обозначаемое
называют число, обозначаемое 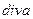 и задаваемое в декартовой системе координат формулой
и задаваемое в декартовой системе координат формулой
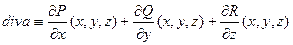 .
.
Значения числовой функции 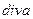 в точках
в точках  не зависят от выбора декартовой системы координат, т.е.
не зависят от выбора декартовой системы координат, т.е. 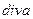 – скалярное поле на
– скалярное поле на 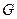 .
.
Определение 19. Ротором (или вихрем) дифференцируемого векторного поля 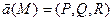 называется вектор
называется вектор
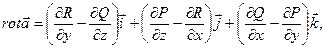
который с помощью символической записи удобно представить в виде векторного произведения
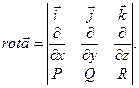
Операторы  называются основными операторами теории поля.
называются основными операторами теории поля.
В математической и особенно физической литературе наряду с введенными операторами широко используется символический векторный дифференциальный оператор набла (оператор Гамильтона)
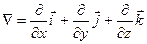 .
.
Правила работы с оператором  такие же, как и с обычными векторами.
такие же, как и с обычными векторами.
Выразим операторы поля через оператор  . Вычисляя произведение вектора
. Вычисляя произведение вектора 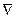 на скалярную функцию
на скалярную функцию 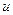 , скалярное и векторное произведения вектора
, скалярное и векторное произведения вектора 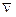 на ветор
на ветор 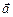 , получим формулы
, получим формулы
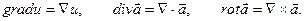
Пример. Для вектора 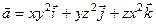 найти
найти 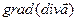 и
и 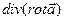 .
.
Решение. 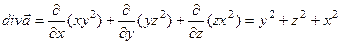 ,
,
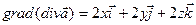 ,
,
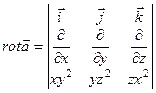
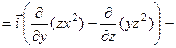
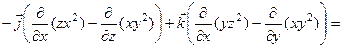
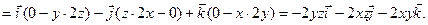

Для потенциального векторного поля 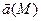 всегда найдется такая скалярная функция
всегда найдется такая скалярная функция 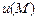 (потенциал векторного поля
(потенциал векторного поля 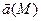 ), что
), что 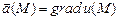 .
.
Потенциал векторного поля  можно найти по формуле
можно найти по формуле
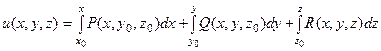 ,
,
где 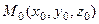 – произвольная точка поля, в которой функции
– произвольная точка поля, в которой функции 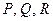 определены..
определены..
Векторное поле называется гармоническим, если во всех точках поля  и
и 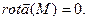
т.е. поле является соленоидальным и потенциальным.
Потенциал 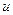 гармонического поля удовлетворяет уравнению Лапласа
гармонического поля удовлетворяет уравнению Лапласа

Вопросы для самопроверки.
1. Какие основные операторы теории поля определяются в этом параграфе? Дайте им определения.
2. Какие из приведенных выше операторов теории поля являются векторными, а какие скалярными величинами?
Задание 17
Пусть заданы функции  и
и 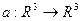 ,
, 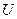 и
и 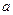 – дифференцируемые функции. Найти:
– дифференцируемые функции. Найти:
a) 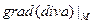 b)
b) 
Не нашли, что искали? Воспользуйтесь поиском: