Замена переменных в тройном интеграле.

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒

Пусть функции

(17)

непрерывны, имеют непрерывные частные производные, якобиан

и сохраняет знак в области определения переменных . Функции (17) биективно отображают область в область. Тогда

В частности, в цилиндрических координатах имеем:

где новые переменные могут принимать значения из промежутков:. При этом. Переход к цилиндрическим координатам в тройном интеграле аналогичен переходу к полярным координатам в двумерном случае.

Замечание. Если тройной интеграл представлен в виде

,

где область зависит от z, так как является ортогональной проекцией D на ось OZ, то пределы интегрирования по и в двойном интеграле при переходе к цилиндрическим координатам, вообще говоря, также должны зависеть от z.

Пример 9. Вычислить тройной интеграл с помощью перехода к цилиндрическим координатам, если область задана неравенствами:.

Решение:

Сферическими координатами называют координаты , связанные с декартовыми координатами формулами:

где – длина радиус-вектора из начала координат в точку , 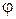– угол проекции радиус-вектора на плоскость ХОУ с положительным направлением оси ОХ (долгота), – угол между радиус-вектором и плоскостью ХОУ (широта). Якобиан при переходе к сферическим координатам в этом случае равен. Тогда для любого жорданова множества 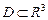и функции имеет место равенство

где

Иногда сферические координаты задают формулами

В этом случае якобиан равен.

Если в пространстве 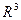задана некоторая жорданова область , ограниченная замкнутой поверхностью, то численное значение объема 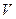такой области вычисляется по формуле

Пример 10. Вычислить объем множества

Решение. Для вычисления объема заданного множества, расставим в интеграле пределы интегрирования в сферической системе координат. V ограниченна сферой и конусом. Множество V лежит выше плоскости z =0, внутри сферы радиуса с центром в точке и внутри конуса. Т.к. обе поверхности, ограничивающие V, есть поверхности вращения относительно Oz, то приведем чертеж сечения V плоскостью y=0.

Перейдем к сферическим координатам в неравенствах, определяющих условия на декартовы координаты точек множества V. Неравенство, задающее шар примет вид. Для внутренних точек конуса получим: или.

Получаем, что сферические координаты должны удовлетворять следующей системе неравенств:

Т.к. и, то получим следующие возможные представления тройного интеграла через повторные:

Вычисления произведём для одного из этих представлений:

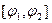
Задание 10

Вычислить объемы тел, ограниченных указанными поверхностями, используя в случае необходимости подходящую замену переменных:

, , , , ,

, , ,

, , ,

, , , ,

, , ,

, , , ,

, ,

, ,

⇐ Предыдущая 1 2 3 4 567 8 Следующая ⇒

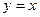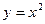
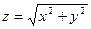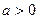
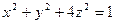
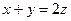
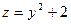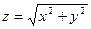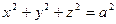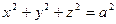Не нашли, что искали? Воспользуйтесь поиском: