
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Приложение 6. Задание 6
Задачи 6.1-6.20
Определить тип и решить дифференциальные уравнения первого порядка. При заданном начальном условии решить задачу Коши. Данные к заданию 6 приведены в Таблице 4.
Таблица4
Данные к заданию 6
| Номер варианта | Дифференциальные уравнения первого порядка |
1) х2(1-у2)dx+y(1+x2)dy=0; 2) xy/=y+xsin2 ( );
3) y/ - 2xy = );
3) y/ - 2xy =  при начальном условии у(0)=3. при начальном условии у(0)=3.
| |
1) (1-у) dx + (1+x) dy =0; 2) у/ =  ;
3) y/ + (tg x) y = ;
3) y/ + (tg x) y =  при начальном условии у(0)=5. при начальном условии у(0)=5.
| |
1) x2yy/ =(x3-1) (y2+5); 2) x у/ -y + 5x  = 0;
3) y/ +y cos x = sin 2x при начальном условии у(0)=2. = 0;
3) y/ +y cos x = sin 2x при начальном условии у(0)=2.
| |
1) y/(5 + 3 y) = xy cos x; 2) y/ =t wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>x</m:t></m:r><m:ctrlPr><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:b/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr></m:ctrlPr></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  ;
3) y/ +2y = 3 ;
3) y/ +2y = 3  при начальном условии у(0)=7. при начальном условии у(0)=7.
| |
1)  (1 + y/) =1; 2) x y/ +x ctg (1 + y/) =1; 2) x y/ +x ctg  = y;
3)y/xlnx – y = 6 x3 ln2x при начальном условии у(e)=2 = y;
3)y/xlnx – y = 6 x3 ln2x при начальном условии у(e)=2  . .
| |
1) x dy + ctg y dx = 0; 2) (x2 – y2) y/ = 2xy;
3) x y/ -3y = x4  при начальном условии у(1) = при начальном условии у(1) =  . .
| |
1) y/ -х lnx y2 = 0;2)у (х2 + у2 ) dx – x3 dy = 0;
3)y/ +   при начальном условии у( при начальном условии у(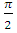 ) = ) =  . .
| |
1) 2  dy – (y2 + 16) dx = 0; 2) (y/ - dy – (y2 + 16) dx = 0; 2) (y/ -  )arctg )arctg  = 1;
3) х y/ -у = 4 х ln x при начальном условии у( = 1;
3) х y/ -у = 4 х ln x при начальном условии у( ) = ) =  . .
| |
1) y/ sin2 x – y ln y = 0; 2) (х2 + у2 + ху) dx – x2 dy = 0;
3) y/ -у ctg x = 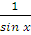 при начальном условии у( при начальном условии у(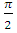 ) = ) = 
| |
1)(5 + y2) dx – (x2 – 4) уdy = 0; 2) (y/ -  )cos )cos  +1=0;
3)y/ + 2xy = +1=0;
3)y/ + 2xy =  при начальном условии у(0)=2. при начальном условии у(0)=2.
| |
1) ( + +  ) y/ -у2 = 0;2)х y/ -у(1 + ln y - ln x) = 0;
3) y/ -у sin x = - sin 2x при начальном условии у(0)=5. ) y/ -у2 = 0;2)х y/ -у(1 + ln y - ln x) = 0;
3) y/ -у sin x = - sin 2x при начальном условии у(0)=5.
| |
1) y/ =  ;2) y/- 1 = exp ( ;2) y/- 1 = exp ( + +  ;
3)х y/ -у = 8 х ln3x при начальном условии у(1)=1. ;
3)х y/ -у = 8 х ln3x при начальном условии у(1)=1.
|
1) y y/ +cos x  = 0;2) y - x y/ = 4 (x + y y/);
3) х2 y/ +2 xу = 7 при начальном условии у(1)=2. = 0;2) y - x y/ = 4 (x + y y/);
3) х2 y/ +2 xу = 7 при начальном условии у(1)=2.
| |
1)dy – y sin2x dx = 0; 2) y/ = 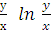 ;
3) y/ + ;
3) y/ +   при начальном условии у(1)= - 2. при начальном условии у(1)= - 2.
| |
1)(e2 x +1)e y y/ -e x(e 2 y – 1) = 0; 2) y/ =  ;
3) y/cos x-у sin x = 1 при начальном условии у(0)=7. ;
3) y/cos x-у sin x = 1 при начальном условии у(0)=7.
| |
1) y/ +  ; 2) х2 y/ = у2 + 3 х у + х2;
3) y/ +у= ; 2) х2 y/ = у2 + 3 х у + х2;
3) y/ +у=  при начальном условии у(0)=1. при начальном условии у(0)=1.
| |
1) y/ =5 х – у;2) х y/ - у = 3 (у y/ + х);
3) y/ +у sinx = 5  при начальном условии у(0)= - 4. при начальном условии у(0)= - 4.
| |
1)(x y2 + 9 x) dx = dy; 2) х y/ -  = y;
3) y/ -2 у = = y;
3) y/ -2 у = 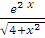 при начальном условии у(0)=ln 2. при начальном условии у(0)=ln 2.
| |
1) y – 2 x y/ =1 + x2 y/;2)х y/ - у = x  ;
3) y/ -у cos x = sin 2 x при начальном условии у(0)=3. ;
3) y/ -у cos x = sin 2 x при начальном условии у(0)=3.
| |
1) y/sin x- (у + 3) cos x = 0; 2) (х2 – 2ху) dy = (x2 + xy- y2) dx;
3) y/ +3 у =  при начальном условии у(0)=1. при начальном условии у(0)=1.
|
Приложение7. Задание 7
Задачи 7.1-7.20
Найти общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами и частное решение, удовлетворяющее данным начальным условиям. Данные к заданию № 6 приведены в Таблице 5.
Таблица 5
Данные к заданию 7
| Номер варианта | Дифференциальное уравнение | Начальные условия |
| y″ - 6 y′ + 9 y = 45 x2 – 42 x - 29 | y(0) = - 1, y′(0) = 9 | |
| y″- 7y′ + 6y = 29 sin x – 11 cos x | y(0) = 0, y′(0) = 11 | |
| 2 y″ + y′ - y = 2 e x | y(0) = - 5, y′(0) = - 8 | |
| y″ - 2 y′ + 2 y = 2 x | y(0) = 6, y′(0) = 3 | |
| y″ - 3 y′ + 2 y = 3 e 2 x | y(0) = - 3, y′(0) = - 7 | |
| 2 y″ + 5 y′ = 29 cos x | y(0) = 2, y′(0) = 10 | |
| y″ + 4 y′ + 4 y = (1 – 4 x) e – 2 x | y(0) = 1, y′(0) = 1 | |
| y″ + y = 2 x3 – x + 2 | y(0) = - 1, y′(0) = - 11 | |
| 5y″ - 6y′ +5y = 20x2–48 x + 65 | y(0) = 8, y′(0) =17/5 | |
| y″ - 2 y′ = e x (x2 + x – 3) | y(0) = 7, y′(0) = - 2 | |
| y″ + y = x sin x | y(0) = 4, y′(0) = - 3 | |
| y″ + y′ - 2 y = cos x – 3 sin x | y(0) = 1, y′(0) = 2 | |
| y″ - 4 y′ + 3 y = e 5 x | y(0) = 3, y′(0) = 9 | |
| y″ - 8 y′ + 16 y = e 4 x | y(0) = 0, y′(0) = 1 | |
| y″ + y = cos 3 x | y(π/2) = 4, y′(π/2) = 1 | |
| y″- 6y′ + 8 y = - 32 x2 + 88 x - 14 | y(0) = 4, y′(0) = 5 | |
| y″ + 4 y = cos 2 x | y(π/4) = 0, y′(π/4) = 1/4 | |
| y″ + 3 y′ - 10 y = 28 x e 2 x | y(0) = 1, y′(0) = - 30 | |
| y″ - 9 y′ +20 y = x2 e 4 x | y(0) = 1, y′(0) = 5 | |
| y″ - 2 y′ + 2 y = e x sin x | y(0) = 1, y′(0) = - 5/2 |
Приложение 8. Задание 8
Задачи 8.1-8.20
Написать три первых члена степенного ряда, найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала.
Данные к заданию 8 приведены в Таблице 6.
Таблица 6
| Номер варианта | Ряд | Номер варианта | Ряд | Номер варианта | Ряд |

| 
| ||||

| 
| 
| |||

| 
| ||||
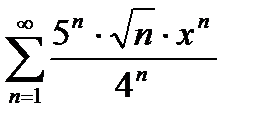
| 
| 
| |||

| 
| ||||

| 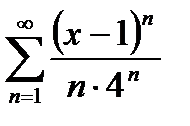
| 
| |||

| 
|
Приложение 9. Задание № 9
Задачи 9.1-9.20
Вычислить с точностью до 0,001 определенный интеграл  , используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда. Данные к заданию 9 приведены в Таблице 7.
, используя разложение подынтегральной функции в степенной ряд и почленное интегрирование полученного ряда. Данные к заданию 9 приведены в Таблице 7.
Таблица 7
Данные к заданию 7
| Номер варианта |  
| Номер варианта | 
|

| 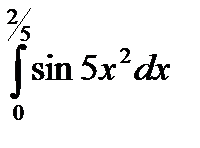
| ||

| 
| ||
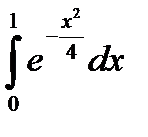
| 
| ||

| 
| ||

| 
| ||
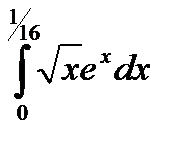
| 
| ||

| 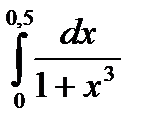
| ||

| 
| ||

| 
| ||

| 
|
Не нашли, что искали? Воспользуйтесь поиском: