СПОКОЙНЫЕ И БУРНЫЕ ПОТОКИ. КРИТИЧЕСКАЯ ГЛУБИНА

Рассмотрим зависимость удельной энергии сечения Э от глубины наполнения h при заданной форме поперечного сечения русла и при
Q = const.

В соответствии с ранее изложенным удельную энергию сечения Э можно рассматривать состоящей из двух часте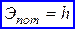й: и 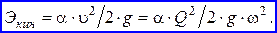Нетрудно заметить, что тенденция их изменения с изменением h диаметрально противоположна, а именно:

при h →0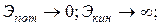

при h →∞

Следовательно, функция Э = f (h) на графике удельной энергии сечения (рис. 12.3) должна иметь вид кривой с двумя ветвями, уходящими в бесконечность при h →0 и при h →∞. При этом 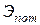отобразится пря­мой – биссектрисой координатного угла, а – некоторой кривой второго порядка.

Линия, характеризующая изменение удельной энергии сечения в зависимости от h, асимптотически приближается к биссектрисе координатного угла и к оси абсцисс и имеет экстремальную точку при некотором значении глубины наполнения.

Глубина потока, при которой удельная энергия сечения для заданного расхода в данном русле достигает минимального значения, называется критической глубиной и обозначается .

Экстремальная точка на графике, соответствующая , делит кривую удельной энергии на две части: верхнюю, где 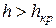, и нижнюю, где . Соответственно принято различать три состояния потока:

1) спокойное состояние, при котором 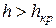, а удельная энергия сечения увеличивается с увеличением ;

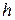2) бурное состояние, когда 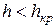, а удельная энергия с увеличением 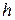уменьшается;

3) критическое состояние при и .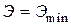

Выявление состояния потока, таким образом, производится путем сопоставления фактического значения 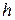с .

Значение критической глубины необходимо не только для определе­ния состояния потока, но и для выполнения ряда гидравлических расчетов, и для анализа в безразмерных координатах результатов исследований.

Для вывода уравнения критического состояния используем, что при 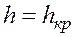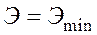, то есть .

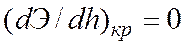Имеем

,

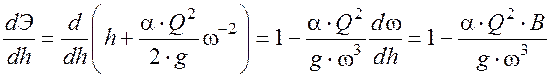так как ранее было сказано, что 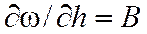; тогда для призматического русла .

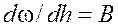Отсюда

или (12.17)

Уравнение (12.17) называется уравнением критического состоя­ния. Для русла произвольной формы в общем виде оно решается подбором или графоаналитически, для русла правильного поперечного сечения возможны простые решения.

Для прямоугольного русла из (рис. 12.4, а) (12.17) имеем:

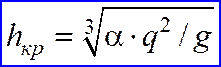(12.18)

где 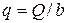– удельный расход, то есть расход на единицу ширины прямоугольного русла.

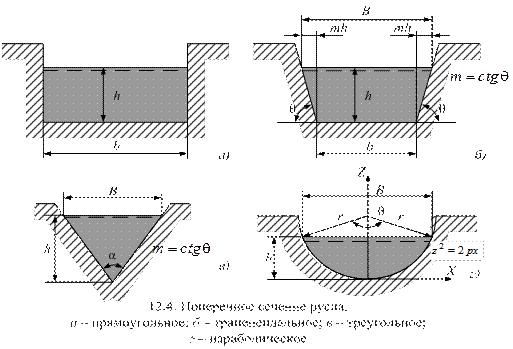
Для трапецеидального русла критическая глубина рассчитывается аналитическим способом, предложенным И. И. Агроскиным. На рис. 12.4, б даны следующие обозначения: b – ширина сечения по дну; h – глубина наполнения; m = ctgθ– коэффициент откоса. Тогда:

.

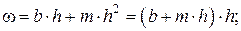
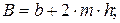
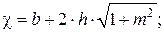
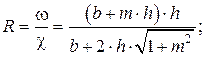
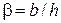Перепишем уравнение (12.7) в виде

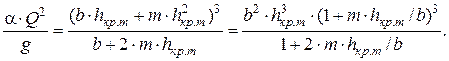(12.19)

Обозначим безразмерное отношение 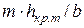через 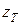. Из (12.19) получим:

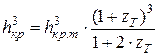
или (12.20)

где – критическая глубина в прямоугольном русле с тем же расходом Q и той же шириной по дну, что и у рассматриваемой трапеции.

По аналогии с 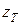введем обозначение 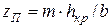для прямоуголь­ного русла (m – коэффициент откоса трапеции). Так же (12.19) получим:

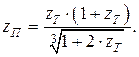(12.21)

Очевидно, что

Задаваясь различными значениями 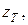можно получить из (12.21) соответствующие 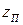и затем значения отношения h_кр.Т / h_кр. Эти значения сведены в табл. 12.1.

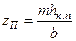
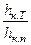
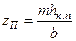
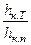
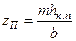
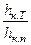
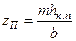
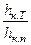
0,005	0,998	0,22	0,931	0,44	0,874	0,80	0,802
0,01	0,997	0,23	0,928	0,45	0,872	0,82	0,799
0,02	0,993	0,24	0,925	0,46	0,869	0,84	0,796
0,03	0,990	0,25	0,922	0,47	0,867	0,86	0,793
0,04	0,987	0,26	0,919	0,48	0,865	0,88	0,789
0,05	0,983	0,27	0,917	0,49	0,862	0,90	0,786
0,06	0,980	0,28	0,914	0,50	0,860	0,92	0,783
0,07	0,976	0,29	0,911	0,52	0,856	0,94	0,780
0,08	0,973	0,30	0,909	0,54	0,852	0,96	0,777
0,10	0,967	0,31	0,906	0,56	0,848	0,98	0,774
0,11	0,964	0,32	0,903	0,58	0,844	1,00	0,771
0,12	0,961	0,33	0,900	0,60	0,839	1,05	0,764
0,13	0,958	0,34	0,898	0,62	0,835	U0	0,757
0,14	0,955	0,36	0,893	0,64	0,831	1,15	0,750
0,15	0,952	0,37	0,890	0,66	0,927	1,20	0,744
0,16	0,949	0,38	0,888	0,68	0,823	1,25	0,737
0,17	0,946	0,39	0,886	0,72	0,816	1,30	0,731
0,18	0,943	0,40	0,884	0,74	0,812	1,35	0,725
0,19	0,940	0,41	0,881	0,76	0,809	1,40	0,719
0,20	0,937	0,42	0,878	0,78	0,806	1,50	0,707
0,21	0,934	0,43	0,876

По найденным h_кр. и 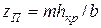определяем h_кр.Т / h_кр. и затем находим h_кр.

Для треугольного русла (рис. 12.4, в) из (12.17) имеем:

(12.22)

Для параболического русла (рис. 12.4, г), описываемого уравнением (р – параметр параболы, имеющий линейную размерность), имеем:

;

,

где – на урезе воды. Тогда:

.

В заключение заметим, что совместное рассмотрение уравнений (12.9) и (12.17) приводит к выводу о равенстве параметра кинетичности единице при критическом состоянии потока, то есть П_к.кр = 1. Таким образом, оценка состояния потока может быть сделана по значению параметра кинетичности, а именно:

П_к < 1 – спокойное состояние потока;

П_к > 1 – бурное состояние потока.

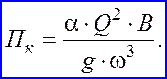(12.9)

(12.17)

46. Критический уклон М.12

КРИТИЧЕСКИЙ УКЛОН

Как видно из изложенного выше, критическая глубина зависит только от геометрической формы поперечного сечения русла и расхода, но не зависит от продольного уклона дна i. Кроме того, в призматическом русле критическая глубина постоянна по всей его длине.

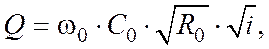(12.11)

При равномерном движении жидкости нормальная глубина, как это следует из (12.11), зависит именно от уклона. Тогда, очевидно, для любого призматического русла (при заданном расходе Q) можно подобрать такое значение i,при котором нормальная глубина h ₀станет равной h_кр.

Критическим уклоном называется уклон, при котором нормальная глубина равна критической.

Для определения i_кр нужно решить совместно уравнения (12.11) (12.17), принимая h ₀ = h_кр:

,

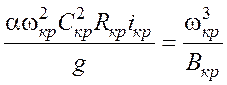откуда

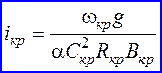
или

так как .

Из уравнения (12.11) следует, что нормальная глубина уменьшается с увеличением i. Поэтому если фактический уклон дна русла i < i_KP,то h ₀ > h_кр и поток при равномерном движении будет находиться в спокойном состоянии. Наоборот, при i > i_кр поток при равномерном движении будет находиться в бурном состоянии, то есть h ₀ < h_кр.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие русла можно отнести к призматическим?

2. Какие русла можно отнести к непризматическим?

3. Запишите дифференциальное уравнение установившегося плавно изменяющегося движения жидкости.

4. Запишите выражение для параметра кинетичности.

5. Какую форму приобретает параметр кинетичности в случае прямоугольного русла?

6. В каком случае происходит движение с образованием кривой подпора?

7. В каком случае происходит движение с образованием кривой спада?

8. В каком случае происходит движение с постоянной глубиной по длине потока?

9. Какую глубину будем называть нормальной глубиной?

10. Запишите выражение для определения удельной энергии сечения.

11. Как будет изменяться удельная энергия сечения для случая ?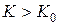

12. Как будет изменяться удельная энергия сечения для случая ?

13. Какая глубина потока называется критической?

14. Какой поток называется спокойный?

15. Какой поток называется бурным?

16. Запишите уравнение критического состояния потока.

17. Запишите выражение для критической глубины потока в случае трапециидального русла.

18. Запишите выражение для критической глубины потока в случае треугольного русла.

19. Запишите выражение для критической глубины потока в случае параболического русла.

20. Какой уклон называется критическим?

МОДУЛЬ 13

РАВНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ
В ОТКРЫТЫХ РУСЛАХ (КАНАЛАХ)

ВВЕДЕНИЕ

Рассмотрим безнапорное установившееся равномерное движение в открытых руслах (включая в это понятие и движение в закрытом русле, частично заполненном жидкостью).

Все открытые русла делятся на естественные и искусственные.

К естественным руслам относятся реки, ручьи, временные водотоки по тальвегам, балкам и пр. Естественные русла характеризуются тем, что очертания ложа русла в живом сечении не имеют какой-либо правильной геометрической формы.

К искусственным руслам относятся каналы, канавы, атакже безнапорные трубы-тоннели, канализационные и дренажные трубы. Характерной особенностью искусственных русел является то, что они, в большинстве случаев, имеют правильную форму поперечного сечения и малую изменяемость площади живого сечения русла.

Изучение всех вопросов, связанных с движением воды в открытых руслах (особенно в каналах) имеет весьма большое практическое значение для гидромелиорации при расчете оросительных, обводнительных и осушительных систем.

Безнапорное движение во всех открытых руслах характеризуется тем, что открытые русла имеют свободную поверхность с одинаковым (атмосферным) давлением.

Равномерным движением в открытом русле будет такое устано­вившееся движение, когда форма и площадь его живого сечения, и, сле­довательно, средняя скорость, остаются постоянными по всей длине русла.

При равномерном движении в открытом русле давление на свободной поверхности по длине не изменяется. Так же постоянно по длине значение скоростного напора 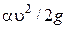. Следовательно, пьезометрический уклон сво­бодной поверхности J_п при равномерном движении равен гидравлическому уклону J, который в свою очередь равен уклону дна i, то есть J = J_n = i.

Равномерное движение характеризуется такими признаками:

1) расход постоянен;

2) русло призматическое;

3) глубина h, и, следовательно,форма и площадь живого сечения w
и c, R постоянны;

4) шероховатость смоченной поверхности по длине не изменяется;

5) отсутствуют местные сопротивления;

6) неизменность положительного (прямого) уклона дна i > 0 по длине.

Условно можно считать, что в призматических каналах указанные условия выполняются. Условность связана с неизбежностью тех или иных местных нарушений равномерности движения (например, вблизи мостов, перегораживающих и других сооружений). Для дальнейшего рассмотрения принимаем, что движение равномерное. Расход при равномерном движении определяют по формуле Шези (12.11)

или по (12.12)

где К ₀ – расходная характеристика при равномерном движении.

Гидравлически наивыгоднейший профиль М.13

Не нашли, что искали? Воспользуйтесь поиском: