ОСНОВНЫЕ ТИПЫ ЗАДАЧ ПРИ РАСЧЕТЕ КАНАЛОВ

Основные типы задач.

Задача первого типа. Заданы все элементы живого сечения, а также i, m, n. Необходимо найти расход Q и среднюю скорость υ.

Задан расход Q, линейные размеры, m и n. Необходимо найти уклон і.

Решение задач этого типа проводится прямой подстановкой вычисленных ω, R, С в (12.11).

(12.11)

– формула Павловского

у – показатель степени

.

Задача второго типа. Заданы Q, m, n, і, один из геометрических элементов живого сечения (b или h для трапецеидального сечения и p или h для параболического). Необходимо найти другой линейный элемент живого сечения, а затем среднюю скорость υ.

Решение ведется с помощью подбора. Задаемся несколькими значе­ниями неизвестного параметра, для каждого из значений находим по формуле Шези (12.11) расход Q. Найдя расход, равный заданному, тем самым определим неизвестный линейный элемент. Расчет можно вести с построением графика зависимости расхода от неизвестного геометрического элемента. Средняя скорость определяется просто. Задача по отысканию ширины трапеции по дну b при неудачном задании h может не иметь решения.

Задача третьего типа. Известны Q, і, m, n. Необходимо найти размеры элементов живого сечения и среднюю скорость υ.

Неопределенность таких задач нейтрализуется введением в них дополнительных условий:

а) канал должен быть гидравлически наивыгоднейшего профиля, то есть иметь 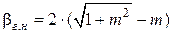для трапециидального или 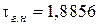для параболического сечения;

б) канал должен иметь заданное отношение β =b/h для трапецеидального или В/h для параболического сечения.

Эти дополнительные условия помогают свести решения этих задач или к использованию уравнения Шези, или к подбору.

Например, для трапецеидального сечения подстановка b= β· h поз­воляет выразить:

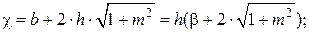
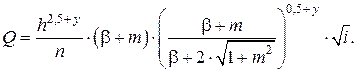
Далее определяется h, затем b и υ.

Задача четвертого типа. Известны Q,υ, і, m, n. Необходимо найти элементы живого сечения.

Определить по известным υ и і, затем по табл. 11 прил. 1 или подбором найти R

(12.11)

найдем b и h из системы уравнений

(13.7)

Для параболического сечения p и h определяются подбором из системы:

(13.8)

Могут встретиться и некоторые промежуточные виды задач. Следует отметить, что метод подбора позволяет получить решение задач равномер­ного движения в открытых руслах произвольной формы при достаточном количестве исходных известных величин.

4. ОСНОВЫ ГИДРАВЛИЧЕСКОГО РАСЧЕТА КАНАЛОВ
В БЕЗРАЗМЕРНЫХ ВЕЛИЧИНАХ

Способ расчета призматических каналов по характеристикам живого сечения был предложен И. И. Агроскиным.

На основании изучения геометрии отдельного живого сечения, пред­ставленного рядом линейных размеров (глубины, средней ширины, гидравлического радиуса и т. п.), можно прийти к заключению, что взаимосвязи отдельных элементов должны проявляться в виде безразмерных величин.

Для установления взаимосвязей необходимо сравнивать расход через данное живое сечение с расходом через какое-либо определенное живое сечение, взятое в качестве эталона.

При гидравлическом расчете каналов любой формы за такой эталон принимается живое сечение той же формы, но гидравлически наивыгоднейшее, то есть с наибольшей пропускной способностью в данных условиях.

Для квадратичной области сопротивления при равномерном движе­нии запишем:

(13.9)

Введем безразмерную величину, равную отношению площади живо­го сечения к квадрату гидравлическому радиуса, и обозначим ее ψ = ω / R ².

Размерные величины ω и R в расходной характеристике представ­ляют собой геометрию живого сечения.

Безразмерная величина ψ может зависеть только от некоторой дру­гой безразмерной величины, которая сама должна полностью характеризовать геометрию живого сечения. Такая безразмерная величина называется характеристикой живого сечения.

Параболическое сечение определяется параметром параболы p, зная который, можно построить параболу по уравнению y ² = 2· p·z. Задавая еще глубину воды h, можно зафиксировать живое сечение. Таким образом, две размерные величины p и h или их безразмерное отношение τ = h / p характеризуют живое сечение.

Величина τ = h / p называется характеристикой живого сечения в па­раболическом русле.

Характеристикой живого сечения трапецеидального русла, также полностью определяющая живое сечение,

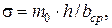(13.10)

где характеристика откоса.

Из всех возможных безразмерных величин, составленных из гео­метрических элементов живого сечения, только τ (для параболического сечения) и σ (для трапецеидального сечения) полностью характеризуют живое сечение данной формы для каждой из характеристик.

Перепишем (13.9) с учетом того, что ω = ψ ·R ². Тогда:

(13.11)

В канале той же формы, с тем же коэффициентом шероховатости, при том же значении но гидравлически наивыгоднейшего профиля будем иметь:

(13.12)

Так как гидравлический радиус максимальный, то при данных значения n и 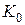величина 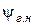должна быть минимальной.

Далее можно найти значения 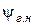для различных форм живого сечения. Из (13.12) можно получить:

(13.13)

Обозначив 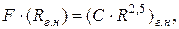получим:

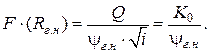(13.14)

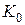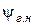Величина может быть найдена или непосредственно из (13.13), или после отыскания по известным и значения . По най­денному значению в табл. 11 приложения найдем величины и затем .

Отметим, что в (13.13) показатель степени 2,5 + у ≈ 2,65 ÷ 2,8. Значение 2,5 + у = 2,7 при расчетах не будет давать отличий, которые надо было бы учитывать, по сравнению с показателями 2,5 и 2,8 до R ≤ 3 м. При больших R целесообразно для расчета принимать точные значения пока­зателя степени 2,5 + у.

Величина принята в рассматриваемом способе расчета в ка­честве основного масштаба. Все элементы каналов выражаются в безраз­мерном виде через .

Из (13.11) и (13.12) имеем:

– безразмерный гидравлический радиус:

(13.15)

– безразмерную площадь:

(13.16)

– безразмерную скорость:

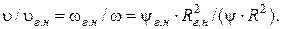(13.17)

Любой элемент живого сечения канала (b, h, , В, p и т.д.) может быть выражен в безразмерные коэффициенты α.

Например, для трапеции:

коэффициенты

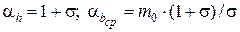и т. д.,

отношение

(13.15а)

Тогда подставив в (13.15) и (13.15а) вместо R величины или 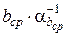и т. д., получим:

(13.18)

(13.19)

Последнее отношение записывают в виде 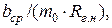для того чтобы в правой части, так же как и для , безразмерные элементы живого сечения были функциями только характеристики живого сечения, в данном случае σ.

(13.20)

Далее, относительная ширина по дну 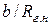зависит от σ и от коэффициента откоса m.

Таким образом была составлена табл. 12 приложения для трапецеидального сечения: задавались значения σ и по выведенным выше формулам вычислялись безразмерные элементы живого сечения. Аналогично получена табл. 13 приложения для параболического сечения, связь между элементами которых дана в § 5.

В каждой такой таблице каждая строчка отражает неограниченное количество живых сечений с разными размерами элементов, но с одной характерной особенностью: эти живые сечения имеют одинаковое значение характеристики живого сечения. Размеры одноименных элементов живых сечений, но их безразмерное выражение для каждого элемента одно и то же.

5. ХАРАКТЕРИСТИКИ ЖИВЫХ СЕЧЕНИЙ С РАЗЛИЧНОЙ ФОРМОЙ
ВЗАИМОСВЯЗИ ЭЛЕМЕНТОВ ЖИВОГО СЕЧЕНИЯ

Выше было показано, что при гидравлически наивыгоднейшем профиле значение безразмерной площади 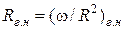минимальное. Поэтому для живых сечений призматических каналов с любой формой необходимо записать ψ как функцию характеристики живого сечения и, выполнив анализ этой функции, из условия 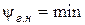найти искомые значения как 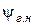, так и характеристики живого сечения гидравлически наивыгоднейшего профиля.

Трапецеидальное сечение. Для живого сечения в виде трапеции имеем:

где – средняя линия трапеции;

Характеристика живого сечения трапецеидальной формы:

,

отражает все факторы, от которых зависит геометрия трапеции.

Характеристика откоса 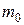равна:

(13.21)

Имеем:

(13.22)

Приравняв нулю, находим:

и (13.23)

Для гидравлически наивыгоднейшего профиля:

Введем относительную ширину трапеции по дну β = b / h и запишем:

(13.24)

или

(13.25)

Тогда для гидравлически наивыгоднейшего профиля ()

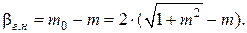(13.26)

Для трапецеидального канала по (13.15)

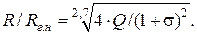(13.27)

Остальные безразмерные элементы канала получаются на основе преобразований, показанных в п. 4.

Основная величина определяется по (13.15):

или

(13.28)

где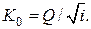

Параболическое сечение. Для такого сечения:

Отсюда:

Приравняв 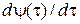нулю, находим, что:

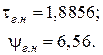(13.29)

Далее находим:

(13.30)

Остальные элементы сведены в табл. 13 приложения.

Круговое (сегментное) сечение. Круговое сечение определяется ради­усом r, для определения живого сечения требуется еще значение глубины h. Но относительная глубина h / r = 2sin²φ/4 (φ – центральный угол сегмента).

Центральный угол φ поэтому принят в качестве характеристики рассматриваемого сечения.

Для сегментного сечения:

(13.31)

Отметим, что полукруг – абсолютно гидравлически наивыгоднейший профиль среди всех возможных форм живого сечения.

6. РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАСЧЕТОВ КАНАЛОВ
ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ

Указанные в п. 3 основные задачи легко решаются с помощью таблиц, составленных И. И. Агроскиным. В задачах первого типа, вычислив R, по табл. 11 приложения находим значение C· , а затем продолжаем вычисления.

Вычисления при решении остальных типов задач начинаются с определения через F· () = Q /(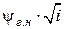) с последующим обращением к табл. 11 приложения по формуле (13.13). Величины C· и C· от формы сечения не зависят.

В задачах второго типа при заданном линейном элементе живого сечения необходимо найти недостающий линейный размер. Находим отношение известного линейного элемента к и по численному значению этого отношения в табл. 12 или 13 приложения (соответствующему данной форме живого сечения) находим значение безразмерного отношения искомого линейного параметра к , найдем искомую величину.

В заданном значении β (для трапеции) и B / h (для параболы) используются формулы, связывающие характеристику живого сечения и заданный параметр. Найдя по вычисленному значению σ соответствующую строку в таблице, принимаем по этой строке все необходимые безразмерные отношения линейных элементов живого сечения к и затем находим значения этих элементов ( найден предварительно).

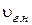При известной величине средней скорости υ (задача четвертого типа) определяются , затем и затем отношение υ/ .

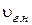По найденной величине υ/ 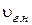аналогично третьему типу задач определяются безразмерные отношения линейных элементов к . Далее находим размеры линейных элементов.

Трапецеидальные каналы гидравлически наивыгоднейшего профиля относительно узкие (см. табл. 13.1), что осложняет их строительство. В связи с этим представляет большой интерес рассмотрение возможности создания трапецеидальных каналов, в которых отношение υ/ 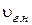было бы незначительно (например, не более 5 %) меньше единицы. Следовательно, в таких каналах ω/ 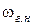незначительно (также не более 5 %) превышает единицу. При столь малых отклонениях от 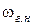(напомним, что она минимальная при данном расходе) отношения b / h при «удалении» от гидравлически наивыгоднейшего профиля резко растут. Поэтому если нельзя запроектировать канал гидравлически наивыгоднейшего профиля, рекомендуется запроектировать канал, назначая требуемое отношение υ/ 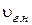(тем самым и ω/ 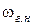), и расчет ведется как для задачи четвертого типа.

Обычно называют ω ≤ (1,01 ÷ 1,05)· 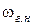. Такого увеличения отношения ω/ 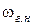в большинстве случаев достаточно для получения приемлемых значений относительной ширины канала.

7. РАСЧЕТ КАНАЛОВ ЗАМКНУТОГО СЕЧЕНИЯ

Равномерное движение в безнапорных водоводах замкнутого сечения характерно для водоотводных труб, туннелей и других конструкций, работающих при неполном заполнении.

В некоторых случаях равномерное движение наблюдается не при всех глубинах.

При равномерном движении расчеты ведутся по формуле Шези с учетом особенностей, присущих только руслам замкнутого сечения. В них при превышении некоторого значения глубины наполнения для круглой трубы (h / d = 0,813) увеличение χ происходит интенсивнее, чем увеличение ω. Вследствие этого гидравлический радиус уменьшается, хотя глубина растет.

Расход и средняя скорость в каналах замкнутого сечения определяются по формулам:

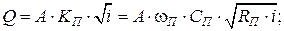(13.32)

(13.33)

где – относительная расходная характеристика;

В = υ / – относительная средняя скорость;

К – расходная характеристика;

υ – средняя скорость при неполном наполнении. Индекс «П» соответствует полному наполнению.

Для круглых труб график зависимости величины А и В от относительной глубины наполнения h / d представлен на рис. 13.1. Очевидно, что рассчитанные значения А и В имеют максимум при h / d = 0,95 (для А) и
h / d = 0,813 (для В).

Однако исследования Н. Ф. Федорова и Ю. М. Константинова показали, что при больших наполнениях расход и средняя скорость имеют меньшие значения, чем вычисленные по (13.32) и (13.33) с использованием А и В из рис. 13.1. Поэтому рекомендуется принимать А и В согласно пунктирным линиям на рис. 13.1.

Дренажные трубы рассчитывают как безнапорные, но полностью заполненные, то есть А = 1. В этом случае при известном расходе 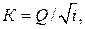а затем определяют необходимый диаметр труб.

Трубы и туннели, для которых применяются замкнутые сечения специальных форм, рассчитываются также по (13.32) и (13.33). Величины А и В при этом принимаются по приводимым в справочниках графикам, соответствующим каждой форме сечения в зависимости от относительной глубины наполнения.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Чем характеризуется безнапорное движение в открытом русле?

2. Какое движение называется равномерным в открытом русле?

3. Какими признаками характеризуется равномерное движение в открытом русле?

4. Запишите формулу для определения расхода при равномерном движении (формулу Шези).

5. Какое сечение называется гидравлически наивыгоднейшим?

6. Какие каналы предпочтительно проектировать с наивыгоднейшим профилем? Почему?

7. Какую скорость принимают под допустимой неразмывающей средней скоростью?

8. Какую скорость принимают за незаиляющую скорость?

9. Какая скорость называется средней незаиляющей скоростью?

10.Что называется гидравлической крупностью наносов?

11.Каким условиям должна удовлетворять средняя скорость в канале?

12.Приведите последовательность решения задачи первого типа.

13.Приведите последовательность решения задачи второго типа.

14.Приведите последовательность решения задачи третьего типа.

15.Приведите последовательность решения задачи четвертого типа.

16.Объясните расчет каналов замкнутого сечения.

МОДУЛЬ 14

Не нашли, что искали? Воспользуйтесь поиском: