
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
кривые спада при < 0.
В зависимости от конкретных условий кривые подпора и спада могут иметь различные особенности. Как отмечено в модуле 12, в зависимости от уклона дна равномерное движение при данном расходе Q может происходить:
а) при спокойном состоянии потока ( >
>  ), если
), если  <
<  ;
;
б) при бурном состоянии потока ( <
<  ), если
), если  >
>  ;
;
в) при критическом состоянии потока ( =
=  ), если
), если  =
=  .
.
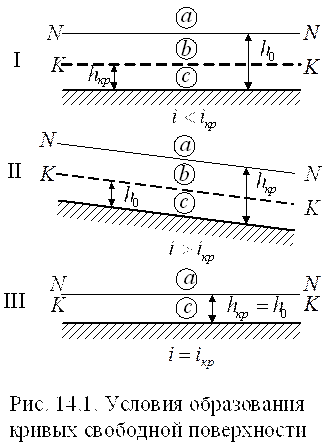
Для анализа условий образования кривых свободной поверхности зафиксируем при  > 0 зоны в потоке, определяемые
> 0 зоны в потоке, определяемые  и
и  (рис. 14.1), проведем также параллельно линии дна линии нормальной NN и критической КК глубин. Тогда получаются следующие зоны, в которых может располагаться кривая свободной поверхности: зона а – выше линии NN и КК; зона b – между линиями NN и КК; зона с – ниже линии NN и КК.
(рис. 14.1), проведем также параллельно линии дна линии нормальной NN и критической КК глубин. Тогда получаются следующие зоны, в которых может располагаться кривая свободной поверхности: зона а – выше линии NN и КК; зона b – между линиями NN и КК; зона с – ниже линии NN и КК.
При  =
=  линии NN и КК совмещены и имеются только зоны а и с. При i > 0 возможны восемь случаев образования кривых свободной поверхности.
линии NN и КК совмещены и имеются только зоны а и с. При i > 0 возможны восемь случаев образования кривых свободной поверхности.
(I случай).
I. Уклон дна  <
<  , то есть при равномерном движении поток находится в спокойном состоянии,
, то есть при равномерном движении поток находится в спокойном состоянии,  >
>  .
.
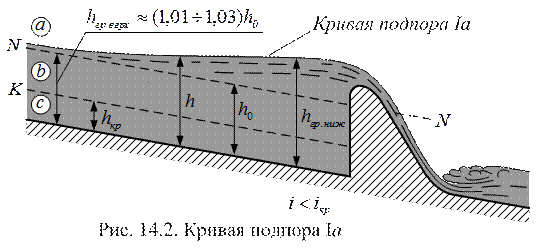
Зона а:  >
>  >
>  (рис. 14.2). Пусть вследствие возведения плотины имевшееся в бытовых (ненарушенных) условиях равномерное движение с глубиной
(рис. 14.2). Пусть вследствие возведения плотины имевшееся в бытовых (ненарушенных) условиях равномерное движение с глубиной  на участке некоторой длины перешло в неравномерное движение с глубинами
на участке некоторой длины перешло в неравномерное движение с глубинами  >
>  . При этом
. При этом  >
> 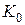 ,
, 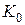 /
/  < 1. Учитываем, что при спокойном состоянии потока
< 1. Учитываем, что при спокойном состоянии потока  < 1, при увеличении h по сравнению с
< 1, при увеличении h по сравнению с  параметр
параметр  будет еще уменьшаться по сравнению с
будет еще уменьшаться по сравнению с  при равномерном движении, поэтому 1 –
при равномерном движении, поэтому 1 –  > 0.
> 0.
Формулу (14.1) условно можно представить только знаками числителя и знаменателя, тогда получим
 .
.
Таким образом, имеем расположенную в зоне а кривую подпора Iа вогнутой формы (так как  > 0). Проанализируем поведение кривой подпора Iа в верхней (по течению) и в нижней (по течению) частях. При
> 0). Проанализируем поведение кривой подпора Iа в верхней (по течению) и в нижней (по течению) частях. При  →
→  получим, что
получим, что  →
→ 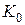 и
и  → 0, то есть кривая подпора Iа в верхней части асимптотически стремится к линии нормальных глубин NN, то есть пересекается с этой линией лишь в бесконечности. Для крупных сооружений на равнинных реках длина кривой подпора может достигать нескольких сотен километров.
→ 0, то есть кривая подпора Iа в верхней части асимптотически стремится к линии нормальных глубин NN, то есть пересекается с этой линией лишь в бесконечности. Для крупных сооружений на равнинных реках длина кривой подпора может достигать нескольких сотен километров.
При возрастании h и К числитель и знаменатель (14.1) стремятся к единицы, так как 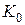 /
/  → 0 и (1 –
→ 0 и (1 –  ) → 1. Тогда
) → 1. Тогда  → i, то есть кривая подпора в нижней части асимптотически стремится к горизонтальной прямой.
→ i, то есть кривая подпора в нижней части асимптотически стремится к горизонтальной прямой.
Зона b:  > h >
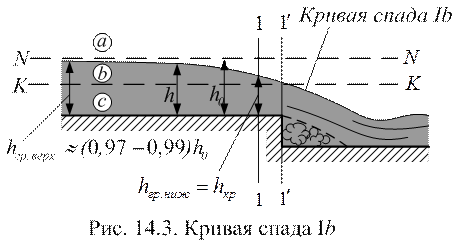
> h >  (рис. 14.3). В этом случае равномерное движение вследствие создания перепада перешло в неравномерное. Здесь
(рис. 14.3). В этом случае равномерное движение вследствие создания перепада перешло в неравномерное. Здесь  <
< 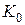 ;
; 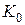 /
/  < 1, а
< 1, а  < 1. Тогда (14.1) можем представить как:
< 1. Тогда (14.1) можем представить как:
 .
.
Глубины по длине потока уменьшаются, то есть в рассматриваемом случае имеем кривую спада Id, располагающуюся в зоне b. Эта кривая асимптотически стремится к линии нормальных глубин NN в верхней своей части, так как  →
→  ,
,  → 0. В нижней части при подходе потока к уступу условия плавной изменяемости, положенные в основу вывода дифференциального уравнения, принимаемого здесь в виде (12.8), не выполняются. Кривизна линий тока становится столь большой, что распределение давления по живому сечению значительно отличается от гидростатического.
→ 0. В нижней части при подходе потока к уступу условия плавной изменяемости, положенные в основу вывода дифференциального уравнения, принимаемого здесь в виде (12.8), не выполняются. Кривизна линий тока становится столь большой, что распределение давления по живому сечению значительно отличается от гидростатического.
Кривая спада Ib располагается в зоне b и обращена выпуклостью вверх. Укажем, что в сечении 1–1, то есть выше уступа на расстоянии, равном
(2 – 2,5)·  , кривая свободной поверхности пересекает линию критических глубин. Строго говоря, применение (15.8) вблизи входа в перепады, то есть на участке между 1–1 и 1'–1', неправильно. При расчете достаточно длинных русл иногда условно считают, что глубина над ребром уступа равна
, кривая свободной поверхности пересекает линию критических глубин. Строго говоря, применение (15.8) вблизи входа в перепады, то есть на участке между 1–1 и 1'–1', неправильно. При расчете достаточно длинных русл иногда условно считают, что глубина над ребром уступа равна  .
.
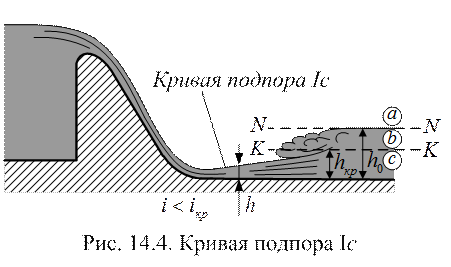
Зона с:  >
>  > h (рис. 14.4). Поток поступает на участок сопряжения бьефов за водосливной плотиной в бурном состоянии, а в естественных (бытовых) условиях находится в спокойном состоянии. От глубины, образующейся у подножья водослива, ниже по течению движения будет неравномерным. Глубины при этом будут увеличиваться, скорости уменьшаться, образуется кривая подпора Iс.
> h (рис. 14.4). Поток поступает на участок сопряжения бьефов за водосливной плотиной в бурном состоянии, а в естественных (бытовых) условиях находится в спокойном состоянии. От глубины, образующейся у подножья водослива, ниже по течению движения будет неравномерным. Глубины при этом будут увеличиваться, скорости уменьшаться, образуется кривая подпора Iс.
Действительно, на участке кривой подпора Iс глубины h <  , то есть
, то есть 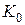 /
/  > 1, а
> 1, а  > 1. Следовательно,
> 1. Следовательно,  > 0. Кривая подпора располагается в зоне с, так как перейти через линию критических глубин плавным образом кривая свободной поверхности не может, что видно на графике изменения удельной энергии сечения Э (см. рис. 12.3). В рассматриваемом случае h <
> 0. Кривая подпора располагается в зоне с, так как перейти через линию критических глубин плавным образом кривая свободной поверхности не может, что видно на графике изменения удельной энергии сечения Э (см. рис. 12.3). В рассматриваемом случае h <  и уменьшение Э до минимума, а затем последующее увеличение удельной энергии сечения и продолжение движения невозможны.
и уменьшение Э до минимума, а затем последующее увеличение удельной энергии сечения и продолжение движения невозможны.
Кривая свободной поверхности имеет вогнутую форму (выпуклостью обращена вниз) и заканчивается в том сечении, где начинается гидравлический прыжок.
Анализ остальных кривых подпора и спада проведем, помня, что каждая кривая свободной поверхности формируется непрерывно только в границах своей зоны.
(II случай).
II. Уклон дна  >
>  , то есть при равномерном движении поток находится в бурном состояния,
, то есть при равномерном движении поток находится в бурном состояния,  <
<  .
.
Зона а: h >  >
>  (рис. 14.5). В этом случае
(рис. 14.5). В этом случае  >
> 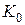 ;
; 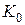 /
/  < 1. Так как h >
< 1. Так как h >  , то в пределах рассматриваемой кривой
, то в пределах рассматриваемой кривой  < 1. Тогда
< 1. Тогда  > 0 и кривая подпора IIа расположена в зоне а. Кривая имеет выпуклую форму, в нижней части асимптотически приближается к горизонтальной линии (снизу от этой линии), так как при h → ∞ отношение
> 0 и кривая подпора IIа расположена в зоне а. Кривая имеет выпуклую форму, в нижней части асимптотически приближается к горизонтальной линии (снизу от этой линии), так как при h → ∞ отношение  → i. Кривая подпора IIа образуется ниже гидравлического прыжка по течению, через который происходит переход потока из бурного состояния в спокойное.
→ i. Кривая подпора IIа образуется ниже гидравлического прыжка по течению, через который происходит переход потока из бурного состояния в спокойное.
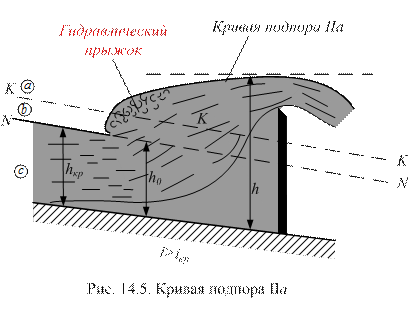
Зона b:  > h >
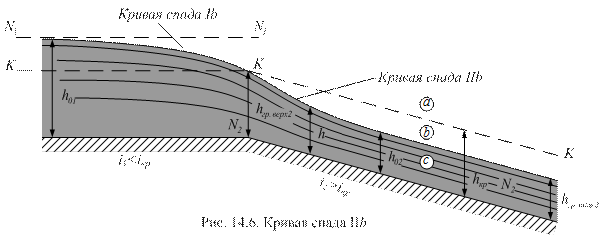
> h >  (рис. 14.6). В этом случае
(рис. 14.6). В этом случае  >
> 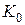 ;
; 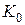 /
/  < 1. При h <
< 1. При h <  параметр
параметр  > 1. Тогда имеем кривую спада IIb.
> 1. Тогда имеем кривую спада IIb.
При h →  кривая асимптотически стремится к линии нормальных глубин NN. Можно считать, что глубина, с которой начинается плавная кривая спада в этой зоне, равна
кривая асимптотически стремится к линии нормальных глубин NN. Можно считать, что глубина, с которой начинается плавная кривая спада в этой зоне, равна  . Ширина канала b на первом и на втором участках канала одинакова. Следовательно,
. Ширина канала b на первом и на втором участках канала одинакова. Следовательно,  будет одной и той же на обоих участках. Но вблизи перелома дна в верхней части кривой движение только условно считается плавно изменяющимся. Кривая спада IIb имеет вогнутую форму.
будет одной и той же на обоих участках. Но вблизи перелома дна в верхней части кривой движение только условно считается плавно изменяющимся. Кривая спада IIb имеет вогнутую форму.
Зона с:  >
>  > h (рис. 14.7). Здесь
> h (рис. 14.7). Здесь  >
> 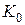 , а
, а  > 1. Тогда
> 1. Тогда  > 0 и имеем кривую подпора IIс. В данном случае начальная глубина
> 0 и имеем кривую подпора IIс. В данном случае начальная глубина  определяется расчетом истечения из-под вертикального плоского затвора. В нижней части кривая IIс асимптотически стремится к линии нормальной глубины, так как при h →
определяется расчетом истечения из-под вертикального плоского затвора. В нижней части кривая IIс асимптотически стремится к линии нормальной глубины, так как при h →  отношение
отношение  → 0. Кривая IIс имеет выпуклую форму.
→ 0. Кривая IIс имеет выпуклую форму.
(III случай).
III. Уклон дна  =
=  , то есть при равномерном движении поток находится в критическом состоянии,
, то есть при равномерном движении поток находится в критическом состоянии,  =
=  . В этом случае имеются лишь две зоны: а и с.
. В этом случае имеются лишь две зоны: а и с.
Зона а: h >  =
=  (рис. 14.8). В этом случае
(рис. 14.8). В этом случае  >
>  ;
;  < 1. Тогда
< 1. Тогда  > 0, то есть имеем кривую подпора. Такая кривая образуется при сопряжении потока, находящегося в критическом состоянии, с потоком, находящегося в русле с
> 0, то есть имеем кривую подпора. Такая кривая образуется при сопряжении потока, находящегося в критическом состоянии, с потоком, находящегося в русле с  <
<  (рис. 14.8). В широких руслах кривая подпора в зоне а близка к горизонтальной прямой.
(рис. 14.8). В широких руслах кривая подпора в зоне а близка к горизонтальной прямой.
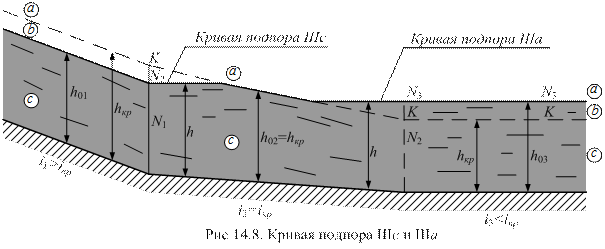
Зона с: h <  =
=  (рис. 14.8). В этом случае
(рис. 14.8). В этом случае  <
< 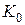 ;
;  > 1. Из уравнения (14.1) имеем
> 1. Из уравнения (14.1) имеем  > 0, и кривая свободной поверхности – кривая подпора III с. Такая кривая создается при сопряжении двух потоков, если уклон подводящего русла
> 0, и кривая свободной поверхности – кривая подпора III с. Такая кривая создается при сопряжении двух потоков, если уклон подводящего русла  >
>  , то есть
, то есть  <
<  , а уклон отводящего русла
, а уклон отводящего русла  =
=  (рис. 14.8). В широких руслах кривая подпора в зоне с также близка к горизонтальной прямой.
(рис. 14.8). В широких руслах кривая подпора в зоне с также близка к горизонтальной прямой.
2. ФОРМЫ СВОБОДНОЙ ПОВЕРХНОСТИ ПОТОКА
В ОТКРЫТЫХ ПРИЗМАТИЧЕСКИХ РУСЛАХ С НУЛЕВЫМ
И ОБРАТНЫМ УКЛОНОМ ДНА
При прямом уклоне дна (i > 0) равномерное движение происходит при равенстве работы силы тяжести в направлении движения и сил сопротивления движению жидкости.
На участке с i ≤ 0 проекция силы тяжести на направление движения равна нулю (при i = 0) или отрицательна (при i < 0). Поскольку на таких участках равномерное движение вообще невозможно, не имеет смысла и понятие нормальной глубины для случаев движения в руслах с i ≤ 0. В связи с этим при i ≤ 0 имеем только две зоны: b и с.
Движение происходит, как и в других случаях, за счет уменьшения удельной (на единицу веса) энергии потока Е, имеющейся в потоке при вступлении на рассматриваемый участок русла.
Удельная энергия потока Е затрачивается на преодоление гидравлических сопротивлений. Удельная энергия сечения Э также будет уменьшаться вниз по течению, как было показано в п. 3 модуля 12.
Поток может вступать на участок с нулевым или обратным уклоном в спокойном или бурном состоянии, так как вступление потока на участок с i ≤ 0 в критическом состоянии энергетически невозможно. Это объясняется тем, что удельная энергия сечения в критическом состоянии минимальна и нет источника энергии для преодоления гидравлических сопротивлений ниже по течению.
Зона b. Поток вступает на участок с i ≤ 0 в спокойном состоянии, h >  . Удельная энергия сечения Э = h +
. Удельная энергия сечения Э = h +  при этом определяется верхней ветвью кривой Э = f (h)(см. рис. 12.3). Уменьшению удельной энергии сечения соответствует уменьшение глубины. Тогда становится ясно, что поток, вступивший на участок с i = 0 или i < 0, может иметь свободную поверхность только в форме кривых спада
при этом определяется верхней ветвью кривой Э = f (h)(см. рис. 12.3). Уменьшению удельной энергии сечения соответствует уменьшение глубины. Тогда становится ясно, что поток, вступивший на участок с i = 0 или i < 0, может иметь свободную поверхность только в форме кривых спада  (при i = 0) или
(при i = 0) или  (при i < 0).
(при i < 0).
Зона с. Поток вступает на участок с i ≤ 0 в бурном состоянии,
h <  . Здесь уменьшение удельной энергии сечения Э возможно лишь при росте глубин [нижняя ветвь кривой Э = f (h)]. Поэтому при вступлении на участок с i ≤ 0 поток в бурном состоянии возможные формы кривой свободной поверхности – только кривые подпора
. Здесь уменьшение удельной энергии сечения Э возможно лишь при росте глубин [нижняя ветвь кривой Э = f (h)]. Поэтому при вступлении на участок с i ≤ 0 поток в бурном состоянии возможные формы кривой свободной поверхности – только кривые подпора  (при i = 0) или
(при i = 0) или  (при i < 0). Итак, в открытых призматических руслах возможны 12 видов кривых свободной поверхности.
(при i < 0). Итак, в открытых призматических руслах возможны 12 видов кривых свободной поверхности.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Изобразите кривую подпора I а и запишите условия ее возникновения.
2. Изобразите кривую спада I b и запишите условия ее возникновения.
3. Изобразите кривую подпора I с и запишите условия ее возникновения.
4. Изобразите кривую подпора II a и запишите условия ее возникновения.
5. Изобразите кривую спада II b и запишите условия ее возникновения.
6. Изобразите кривую подпора II c и запишите условия ее возникновения.
7.
[1], согласно формуле Дарси-Вейсбаха
Не нашли, что искали? Воспользуйтесь поиском: