
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
РАСЧЕТ НАДЕЖНОСТИ СИСТЕМ ПО КРИТЕРИЮ РАБОТОСПОСОБНОСТИ
Цель работы: научиться рассчитывать надежность (безотказность) систем с различным соединением элементов.
Задачи работы:
1. Изучить теоретические основы расчета вероятности безотказной работы систем с различным соединением элементов.
2. Приобрести навыки формализации технических систем в структурные и функциональные схемы.
3. Провести расчеты вероятности безотказной работы систем с различным соединением элементов.
Теоретическая часть [ 3, 4, 5, 10 ]
Техническая система (ТС)– сложный объект, представляющий собой совокупность взаимосвязанных функционально и расположенных в определенном порядке объектов.
Элемент (технической системы) – объект, представляющий собой часть ТС в конкретном рассматриваемом исследовании.
Исправное состояние (исправность) – состояние объекта, при котором он удовлетворяет всем требованиям нормативно-технической документации (НТД).
Неисправное состояние (неисправность) – состояние объекта, при котором он не удовлетворяет хотя бы одному из требований НТД.
Работоспособное состояние (работоспособность) – состояние объекта, при котором значения всех параметров, характеризующих его способность выполнять заданные функции, соответствуют требованиям НТД.
Неработоспособное состояние (неработоспособность) – состояние объекта, при котором значение хотя бы одного параметра, характеризующего его способность выполнять заданные функции, не соответствуют требованиям НТД.
Предельное состояние – состояние объекта, при достижении которого его дальнейшее применение по назначению недопустимо или невозможно.
Повреждение – событие, заключающееся в нарушении исправности объекта при сохранении его работоспособности.
Отказ – событие, заключающееся в нарушении работоспособности объекта.
Автомобили в периоды их использования, хранения, транспортирования, ТО и ремонта в течение всего срока службы всегда находятся в одном из рассмотренных выше четырех состояниях. Особым видом неработоспособного состояния является предельное состояние. Переход из одного состояния в другое фиксируется событиями – повреждением или отказом.
Ремонтируемый объект – объект, для которого возможность проведения ремонтов и ТО предусмотрена в НТД.
Автомобили относятся к классу ремонтируемых объектов.
Неремонтируемый объект – объект, для которого возможность проведения ремонтов и ТО не предусмотрена в НТД.
К ним могут быть отнесены подшипники качения, шпонки, клиновые ремни, манжеты, уплотнения и т.д., нарушение работоспособности которых по критерию прочности или предельного износа соответствует их переходу в предельное состояние с последующей сдачей в утиль.
Показатель надежности – величина, характеризующая одно из свойств (единичный показатель) или несколько свойств надежности (комплексный показатель).
Наработка – это продолжительность или объем работы изделия. Для автомобиля естественно исчисление наработки в километрах пробега, тогда как для других технических средств могут быть удобнее иные единицы измерения (например, наработка радиоэлектронных систем измеряется в единицах времени, наработка станков – в единицах выпущенной продукции).
Безотказность изделий характеризуется следующими показателями: вероятностью безотказной работы, интенсивностью отказов, наработкой до отказа, наработкой на отказ.
Вероятность безотказной работы (ВБР) – вероятность того, что в пределах заданной наработки (срока службы) отказ в изделии не возникает. Символически это определение можно записать в виде формулы (1.1):
Р(t) = p(Q > tз), (1.1)
где Q - случайное время (наработка) возникновения отказа;
tз – заданное время (наработка).
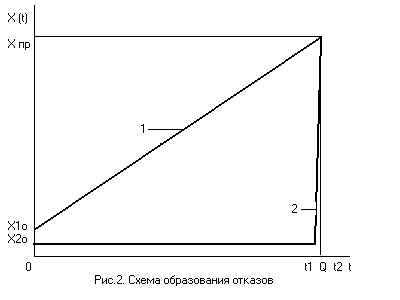
Графически интерпретировать это определение можно с помощью рис.1.4, где условно показан характер возникновения 1 - постепенного и 2 - внезапного отказов. На рис. 1.4 Х 1,0, Х 2,0 соответствуют начальным значениям каких-либо параметров изделия, а Х ПР – предельному значению параметра.
Кроме ВБР при оценке безотказности изделий используется и другая вероятность – вероятность отказа (ВО). Вероятность отказа - это вероятность события, противоположного работоспособности изделия.
Вероятностью отказа (ВО) называется вероятность того, что случайное время возникновения отказа Q (см. рис. 1.4) окажется меньше заданного времени t2, т.е.
F(t) = p(Q < t2). (1.1)
| Рис. 1.4. Схема формирования отказов |
Таким образом, ВБР и ВО являются вероятностями двух противоположных событий, следовательно вполне справедлива формула
(1.2):
Р (t) + F (t) = 1. (1.2)
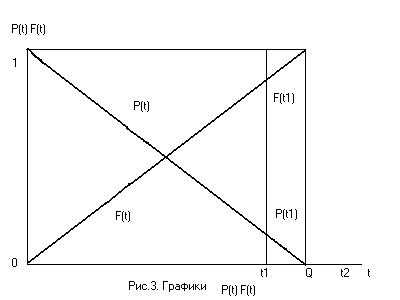
Графическая интерпретация ВБР Р(t) и ВО F(t) показана на рис. 1.5.
| Рис. 1.5. График зависимости P(t) и F(t) |
ВБР можно рассчитать по статистической формуле (1.3):
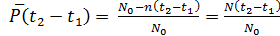 , (1.3)
, (1.3)
где No – число изделий до начала испытаний (наблюдений);
t2 – t1 – отрезок времени (наработки), в течение которого велись испытания (наблюдения);
n(t2 – t1) – число изделий, отказавших за время (t2 – t1).
По формуле (1.3) можно определить ВБР только за отрезок времени (t2 – t1) и невозможно определить Р(t) за другой период времени.
В вероятностной постановке, ВБР и ВО, с учетом того, что изделия имеют наработку до отказа Т, а t является заданной наработкой, т.е. вероятность Вер(T ³ t), будут между собой связаны следующим соотношением.

Прогнозировать ВБР можно на основе теоретических зависимостей, когда известны законы распределения времени возникновения отказов.
Интенсивность отказов (lt) – отношение числа изделий n(t), отказавших в единицу времени, к среднему числу изделий N СР, исправно работающих в данный отрезок времени D t, при условии, что отказавшие изделия не восстанавливаются и не заменяются новыми т.е.

где n(t) – число отказавших изделий за время D t (в интервале t…t+Dt);
D t – интервал времени;
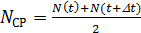 , (1.5)
, (1.5)
где N(t) – количество изделий до начала испытаний (наблюдений);
N(t+Dt) = N(t) – n(t) – количество работоспособных изделий, оставшихся после испытаний.
| Рис. 1.6. График интенсивности отказов по периодам эксплуатации |

Для многих элементов `l(t) имеет закономерность, приведенную на рис. 1.6, где можно выделить три характерные периода:
(0... t1) - (1-й период) – участок приработки. На этом участке l(t) определяется функцией;
(t1…t2) – (2-й период) – участок нормальной эксплуатации.
Для многих элементов в этот период имеют место только внезапные отказы. Следовательно, на этом участке интенсивность отказов может быть найдена по следующей формуле:
 (1.6)
(1.6)
Интегрируя (1.6), легко получить:
 . (1.7)
. (1.7)
Это выражение является одним из основных уравнений теории надежности. В частном случае постоянства интенсивности отказов v(t)=λ= const (1.5) переходит в известное в теории вероятностей экспоненциальное распределение:
P (t)=e–v t; F (t)=1–e–v t; f (t)=ve–v t (1.8)
после t 2 – (3-й период), в течение которого к внезапным отказам добавляются еще постепенные отказы, связанные с повышенным износом и старением. В этом периоде l(t) непостоянна, определяется функцией.
Понятие интенсивности отказов используется в основном невосстанавливаемых изделий.
Для восстанавливаемых изделий используется понятие параметра потока отказов w (t), которым называется отношение изделий, отказавших в единицу времени, к числу испытываемых изделий при условии, что все отказавшие изделия восстанавливаются и продолжают работать. На основе этого имеем:
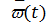 =
= 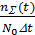 = f(t), (1.9)
= f(t), (1.9)
то есть `w(t) численно равен ¦(t),
где n å(t) – число всех отказов, полученных за время Dt;
N o – число изделий, участвующих в испытаниях.
Поток отказов при v(t)=const называется простейшим. Он реализуется в течение периода нормальной эксплуатации от окончания приработки до начала периода повышенного старения и износа (см. рис. 1.6). Простейший параметр потока отказов, который характеризуется тремя основными свойствами – стационарностью, ординарностью и без последействием:
1- если w (t) = const, то поток считается стационарным;
2– если вероятность возникновения одновременно двух отказов близка к нулю, то поток называется ординарным;
3 – если отказы независимы, то поток считается без последействия.
Для простейшего потока отказов применим закон Пуассона:
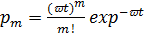 , (1.10)
, (1.10)
где pm - вероятность возникновения m отказов за время t.
Наработка до отказа (среднее время безотказной работы) Тср, `Т (для не восстанавливаемых изделий) – среднее значение наработки изделия между отказами при условии восстановления каждого отказавшего элемента.
В вероятностной постановке:
 (1.11)
(1.11)
где t – значения наработки до отказа;
P (t) – вероятность безотказной работы (см. (1.8));
f (t) – плотность распределения наработки до отказа, характеризующая распределение отказов во времени:
 , (1.12)
, (1.12)
где F (t)=Вер(T < t) – функция распределения наработки до отказа (Вер(T < t) – вероятность того, что наработка до отказа T меньше заданного значения t);
Q (t) – вероятность отказа в течение наработки t;
d Q – вероятность отказа в течение времени d t;
d n (t)– число отказавших изделий в течение времени d t.
В статистической постановке может определяться по формуле (1.13):
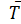 i =
i = 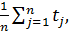 (1.13)
(1.13)
где n - число отказов в каждом i - м изделии;
tj – наработка (ВБР) между (j – 1)-м j -м отказами.
Средняя наработка на отказ T 0 (для восстанавливаемых изделий) – это отношение наработки восстанавливаемого изделия к математическому ожиданию числа его отказов в течение этой наработки. Другими словами, средняя наработка на отказ – это математическое ожидание наработки изделия до очередного отказа после начала эксплуатации или ремонта.
В вероятностной трактовке:
 , (1.14)
, (1.14)
где t – значения наработки на отказ;
f (t) – плотность распределения наработки на отказ (по другому – плотность вероятности отказа) – величина, характеризующая распределение отказов во времени и определяющаяся аналогично плотности распределения наработки до отказа (отличие заключается только в том, что аргумент t в этом случае является наработкой на отказ).
Подставив выражение плотности вероятности f (t) экспоненциального распределения (1.8) в (1.14), получим:
 , (1.15)
, (1.15)
т.е. при простейшем потоке отказов средняя наработка Т 0 обратно пропорциональна интенсивности отказов l. С помощью (1.8), также можно показать, что за время средней наработки t=T 0 вероятность безотказной работы изделия составляет 1/е.
Часто используют показатель, называемый g -процентной наработкой – наработкой, в течение которой отказ не наступит с вероятностью g(%):
 (1.16)
(1.16)
Выбор показателя для количественной оценки надежности определяется назначением, режимами работы изделия, удобством применения в расчетах на стадии проектирования.
Большинство технических объектов, в том числе автомобили, являются системами, состоящими из отдельных узлов, деталей, агрегатов, устройств контроля, управления и т.д. (элементов). Расчленение системы на элементы достаточно условно и зависит от постановки задачи расчета надежности. Например, при анализе работоспособности технологической линии ее элементами могут считаться отдельные установки и станки, транспортные и загрузочные устройства и т.д.. В свою очередь станки и устройства также могут считаться техническими системами и при оценке их надежности они должны быть разделены на элементы – узлы, блоки, которые, в свою очередь – на детали.
При определении надежности системы в первую очередь необходимо оценить влияние каждого элемента на работоспособность системы в целом. С этой точки зрения целесообразно разделить все элементы на четыре группы:
1. Элементы, отказ которых практически не влияет на работоспособность системы (например, деформация кожуха, изменение окраски поверхности и т.п.).
2. Элементы, работоспособность которых за время эксплуатации практически не изменяется и вероятность безотказной работы близка к единице (корпусные детали, малонагруженные элементы с большим запасом прочности).
3. Элементы, ремонт или регулировка которых возможна при работе изделия или во время планового технического обслуживания.
4. Элементы, отказ которых сам по себе или в сочетании с отказами других элементов приводит к отказу системы.
Очевидно, при анализе надежности системы имеет смысл включать в рассмотрение только элементы последней группы.
По способности систем продолжать выполнять свои функции при отказе одного или нескольких элементов все системы делятся на системы типа«m из n», мостиковые и комбинированные.
Система типа “m из n” способна выполнять свои функции, если из n ее элементов работоспособными окажутся любые m и более элементов. В электрических системах и системах связи, технологических линиях наиболее часто встречаются системы типа “ m из n ” при m < n.
Вариантами систем типа “ m из n ” являются последовательные системы (в этом случае m = n) и параллельные системы (m =1).
Последовательная система – это система типа “ n из n ”. Отказ любого элемента этой системы приводит к отказу всей системы. Примером последовательной системы служат: последовательно соединенные электрические лампы; система подшипников.
Параллельная система – это система типа “1 из n ”. Отказ параллельной системы наступает при отказе всех ее элементов. Примером параллельной системы служат: параллельно соединенные электрические лампы; резервированные системы.
Мостиковая система представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей (рис. 2.7). Работоспособность такой системы нарушается при возникновении определенной комбинации отказов ее элементов.
Комбинированная система – это система, состоящая из подсистем типа «m из n» имостиковых подсистем. Для отказа такой системы необходимо возникновение определенной комбинации отказов. Примеры: смешанно соединенные электрические лампы; частично резервированные системы.
Надежность систем графически можно изобразить с помощью структурной схемы надежности. Отдельные блоки этой схемы соответствуют элементам системы, в которых может произойти отказ. Блоки последовательной системы соединяются последовательно (порядок соединения может быть выбран произвольно), блоки параллельной системы – параллельно.
На рис. 1.7 представлена структурная схема надежности последовательной системы. Если на вход такой системы подать сигнал и условно предположить, что исправные элементы пропускают его, а неисправные – нет, то на выход системы входной сигнал пройдет только в случае безотказной работы всех элементов системы. Вероятность безотказной работы данной системы равна: Р = Р (А 1∙ А 2∙...∙ Аn), где А 1, А 2,... Аn – события, заключающиеся в безотказной работе соответствующего элемента системы.
На рис.1.8 представлена структурная схема надежности параллельной системы. Вероятность безотказной работы данной системы равна: Р = Р (А 1+ А 2+...+ Аn).
На рис. 1.9 представлена структурная схема надежности системы типа “2 из 5”, которая работоспособна, если из пяти её элементов работают любые два, три, четыре или все пять (на схеме пунктиром обведены функционально необходимые два элемента, причем выделение элементов 1 и 2 произведено условно, в действительности все пять элементовравнозначны).
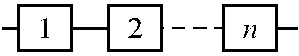
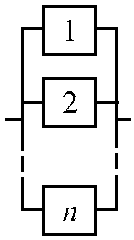
| Рис 1.7. Структурная схема надежности последовательной системы | Рис. 1.8. Структурная схема надежности параллельной системы |
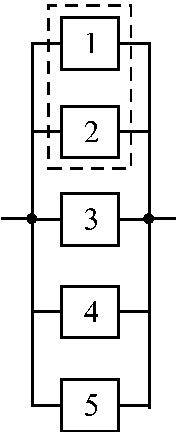
Рис. 1.9. Структурная схема надежности системы типа “2 из 5”
На рис.1.10, а представлена структурная схема надежности мостиковой системы. Работоспособность этой системы будет утрачена при одновременном отказе элементов (1 и 2) или (4 и 5) или (2, 3 и 4) и т.д. В то же время отказ элементов (1 и 5) или (2 и 4) или (1, 3 и 4) или (2, 3 и 5) к отказу системы не приводит.
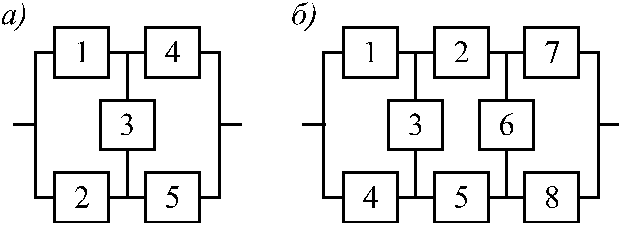
Рис. 1.10. Структурные схемы надежности мостиковых систем
На рис. 1.11 представлена структурная схема надежности комбинированной системы. Вероятность безотказной работы данной системы равна: Р = Р ((А 1+ А 2+ А 3)× А 4)
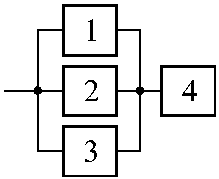
Рис. 1.11. Структурная схема надежности комбинированной системы
Конечной целью расчета надежности технических устройств является оптимизация конструктивных решений и параметров, режимов эксплуатации, организация технического обслуживания и ремонтов. Поэтому уже на ранних стадиях проектирования важно оценить надежность объекта, выявить наиболее ненадежные узлы и детали, определить наиболее эффективные меры повышения показателей надежности. Решение этих задач возможно после анализа структурных схем надежности проектируемых систем. Этот анализ, как правило, включает следующие операции.
1. Система делится на элементы.
2. Определяются возможные отказы элементов, их причины и последствия.
3. Определяются показатели надёжности элементов.
4. Оценивается влияние отказов элементов на работоспособность системы.
5. Составляется структурная схема надежности технической системы.
6. По надежности элементов в соответствии со структурной схемой надежности вычисляются показатели надёжности системы.
На основании результатов расчета показателей надежности системы делаются выводы и принимаются решения об изменении или доработке элементной базы, резервировании отдельных элементов или узлов, об установлении определенного режима профилактического обслуживания, о номенклатуре и количестве запасных элементов для ремонта и т.д.
Не нашли, что искали? Воспользуйтесь поиском: