
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
A. Бінарныя алгебрычныя аперацыі. Асацыятыўныя, камутатыўныя аперацыі; нейтральны элемент, сіметрычны элемент. Азначэнні, прыклады, ўласцівасці.
Азн.1: Няхай Х-непустое мноства.Будзем казаць, што на мностве Х вызначана бінарная алгебрычная аперацыя, калі кожнай спарадкаванай пары (a,b) элементаў мноства Х пастаўлены ў адпаведнасць адназначна вызначаны элемент з мноства Х.
Такім чынам, бінарная алгебрычная аперацыя на мностве Х – гэта f: Х  Х
Х  Х.
Х.
Вобраз пары (а,b) f(а,b) будзем называць кампазіцыяй элементаў а,b і абазначаць а  b.
b.
Калі аперацыя на мностве называецца множаннем (складаннем), тады кампазіцыю а  b будзем называць здабыткам (сумай) і абазначаць аb (а
b будзем называць здабыткам (сумай) і абазначаць аb (а  b).
b).
Прыклады бінарных алгебрычных аперацыяў:
1) Складанне і множанне на мноствах: N, Z, Q, R, C, R[x], Rn*n
2) Адыманне на мноствах: Z, Q, R, C, R[x], Rn*n
3) Дзяленне на мноствах: Q*= Q\{0}, R*= R\{0}, C*= C\{0}.
Азн.2: Будзем казаць, што элемент n 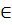 Х з’яўляецца нейтральным у дачыненні да бінарнай алгебрычнай аперацыі
Х з’яўляецца нейтральным у дачыненні да бінарнай алгебрычнай аперацыі  , калі для кожнага а
, калі для кожнага а 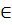 Х, а
Х, а  n= n
n= n  а= a.
а= a.
Прыклады:
1)Для мностваў Z, Q, R, C нейтральны элемент у дачынненні да аперацыі: складання - 0, множання – 1.
2) Для R[x] нейтральнымі элементамі у дачынненні да складання і множання будуць адпаведна нулявы паліном і паліном нулявой ступені, роўны 1.
3) Для Rn*n нейтральным элементам у дачынненні да складання і множання служаць нулявая і адзінкавая матрыцы.
Сцв.1: Для адвольнай бінарнай алгебрычнай аперацыі  не больш за адзін нейтральны элемент.
не больш за адзін нейтральны элемент.
Азн.3:Бінарная алгебрычная аперацыя  на мностве Х наз. асацыятыўнай, калі для адвольнага a,b,c
на мностве Х наз. асацыятыўнай, калі для адвольнага a,b,c 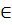 X, a
X, a  (b
(b  c)=(a
c)=(a  b)
b)  c.
c.
Сцв.2: Калі бінарная алгебрычная аперацыя асацыятыўна, тады для адвольных натуральных n и i, 1  i
i  n:
n:
(a1  a2
a2 
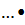 ai)
ai)  (ai+1
(ai+1  an) = a1
an) = a1  a2
a2  an.
an.
Азн.4:Няхай на мностве Х вызначана бінарная алгебрычная аперацыя 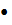 ,якая мае нейтральны элемент n.Элемент а1
,якая мае нейтральны элемент n.Элемент а1 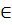 Х наз сіметрычным да элементу а
Х наз сіметрычным да элементу а 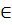 Х у дачыненні да аперацыі
Х у дачыненні да аперацыі 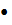 , калі a
, калі a  а1=а1
а1=а1  а=n.
а=n.
Калі а1 - сіметрычным да элементу а, тады а -сіметрычным да элементу а1.
Сцв.3: Калі бінарная алгебрычная аперацыя на мностве Х асацыятыўна, тады для кожнага а 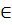 Х існуе не больш за адзін сіметрычны элемент.
Х існуе не больш за адзін сіметрычны элемент.
Калі аперацыя называецца множаннем, тады сіметрычны да а элемент называюць адваротным і абазначаюць а-1, калі аперацыя называецца складаннем, тады сіметрычны да а элемент называюць супрацьлеглым і абазначаюць -а.
Азн.5: Бінарная алгебрычная аперацыя  на мностве Х, наз. камутатыўнай, калі для адвольных элементаў a,b
на мностве Х, наз. камутатыўнай, калі для адвольных элементаў a,b 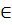 X:
X:
a  b=b
b=b  a.
a.
Прыклады:
1) Аперацыі “+” і “*” на мноствах Z, Q, R, C, R[x]– камутатыўныя.
2) На Rn*n “+” – камутатыўнае, а “*” для n>1 – некамутатыўнае.
Не нашли, что искали? Воспользуйтесь поиском: