ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Калі -элемент бясконцага парадку,тады група ( ) – бясконцая і для n≠k n,k .
Заўвага: Калі 
- элемент парадку 
, тады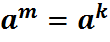 
.
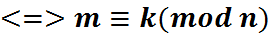У прыватнасці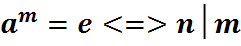 
.
Тэарэма3: Кожная падгрупа цыклічнай групы -цыклічная.
Сцв.2: Няхай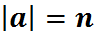 
. Для адвольнага k 
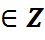парадак 
.
Сцв.3: У цыклічнай групе парадку n, для адвольнага натуральнага k, k | n існуе адзіная падгрупа парадку k.
Тэарэма 5: 1) Адвольная бясконцая цыкічная група ізаморфная адытыўнай групе Z;
2) Адвольная канцоўная цыклічная група парадку n ізаморфная групе C(n) камплексных каранёў ступені n з адзінкі.
A. Сіметрычная група. Раскладанне падстановы ў здабытак незалежных цыклаў (без доказу). Парадак падстановы. Цотнасць падстановы (без доказу карэктнасці азначэння цотнасці). Зменназнакавая група.
Няхай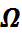 
непустое мноства. Мноства 
усіх біекцыяў 
ёсць группа ў дачыненні да аперацыі множання адлюстраванняў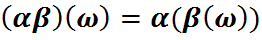 
, для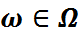 
- сіметрычная група мноства .
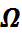Яе элементы наз. падстановамі мноства .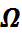
Калі 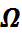- канцоўнае мноства прадку n, тады таксама абазначаюць 
і наз. сіметрычная група ступені n.
Падстанову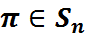 
абазначым 
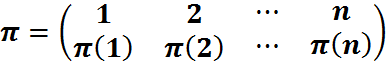. З таго, што 
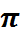- падстанова, г.зн. біекцыя вынікае 
– перастаўленне лікаў 1,2,…,n. Значыць лікі 1,2,…,n сустракаюцца адзін і толькі aдзін раз.
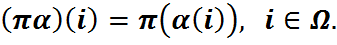
Тэарэма1: Парадак групы роўны n! 
.
Азн.1: Падстановы 
наз. незалежнымі, калі
.
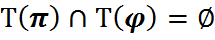Азн.2: Няхай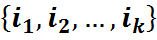 
- падстанова з k элементаў мноства 
= 
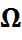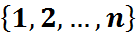. Падстанова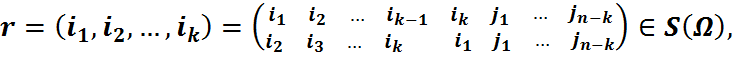 
дзе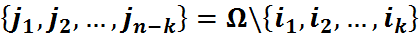 
, наз. цыклам даўжыні k.
Азн.3: Цыклы (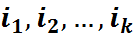 
) і ( 
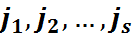) наз. незалежнымі ці неперасякальнымі, калі 
. Незалежныя цыклы перастановачныя.
Тэарэма2: Адвольная падстанова 
раскладаецца ў здабытак незалежных цыклаў даўжыні, больш за 1. Гэты расклад адназначны з дакладнасцю да парадку сумножніка.
Вынік1: Парадак падстановы 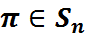роўны найменшаму супольнаму кратнаму даўжыняў незалежных цыклаў, якія ўваходзяць у расклад .
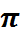Азн.4: Цыкл даўжыні 2 наз. транспазіцыяй.
Вынік2: Кожная падстанова з 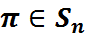раскладаецца ў здабытак транспазіцыяў.
Азн.5: Функцыя f(x1,x2,…,xn), вызначаная на камутатыўным колцы, наз. косасіметрычнай, калі r 
f=-f для адвольнай транспазіцыі r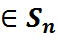 
.
Лема:Няхай.Тады.
Тэарэма3: Няхай ,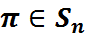 
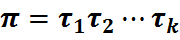– некаторы расклад 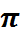у здабытак транспазіцыяў. Тады цотнасць ліку k цалкам вызначаецца падстановай 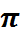і не залежыць ад раскладу .
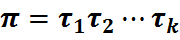Азн.6: Падстанова наз. цотнай, калі яна раскладацца ў здабытак цотнай колькасці транспазіцыяў, і няцотнай, калі яна раскладаецца ў здабытак няцотнай колькасці транспазіцыяў.
Вынік: Усе цотныя падстановы ступені складаюць падгрупу 
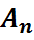групы парадку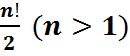 
.
Група 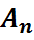наз. зменназнакавай групай ступені n.
Не нашли, что искали? Воспользуйтесь поиском: