A. Гомамарфізмы групаў. Азначэнне, прыклады, уласцівасці.

Азн.1: Няхай G і - групы з аперацыямі • і * адпаведна. Адлюстраванне наз. гомамарфізмам групы G у групу , калі для адвольных элементаў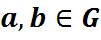

.

Прыклады:

1) Няхай G і – адвольныя групы. Адлюстраванне 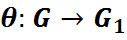такое, што для адвольнага . Дзе – адзінка , відавочна, гомамарфізм групаў. Ён наз. нулявым гомамарфізмам;

2) Калі H – падгрупа групы G, тады адлюстраванне 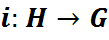такое, што для - ін’екцыіны гомамарфізм групаў. Яго наз. укладаннем у групу .

3) Адлюстраванне : , дзе - гомамарфізм.

Бо для адвольных камплексных лікаў .

Уласцівасці гомамарфізмаў групаў:

Калі – гомамарфізм групаў, тады:

1) , дзе e, - адзінкі групаў адпаведна.

2) .

3) Калі H – падгрупа групы G, тады – падгрупа групы , у прыватнасці, – падгрупа групы - вобраз гомамарфізму

4) Калі 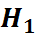- падгрупа групы поўны правобраз - падгрупа групы G.

5) Калі H⊲ G, тады .

6) Калі .

7) Калі – гомамарфізм групаў, тады 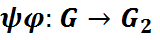– гомамарфізм групаў.

Азн.2: Няхай - гомамарфізм групаў, - адзінкі групаў . Мноства =Ker 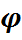наз. ядром гомамарфізму

Тэарэма1: Няхай G і – групы, – гомамарфізм. Ядро гомамарфізму 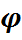- нармальная падгрупа групы G.

Не нашли, что искали? Воспользуйтесь поиском: