Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса.

Метод Гаусса – метод послед-го исключ.переменных. Сначала(на 1-м шаге прямого хода Гаусса) из всех ур-ний,кроме 1-го исключается переменная х₁. Потом (на 2 шаге) из всех ур-й,кроме первых 2-х исключается переменная х₂ и т.д.,пока последнее ур-е не приобретёт вид: С _* Х_n=b_m, если ч-ло С=0, а b_m не=0,то с-ма не совместная,т.е.нет решений. Если С=0 и b_m=0,т.е. 0_*Х_n=0,то с-ма неопределённая,т.е. имеет бескон.мн.реш.,то с-ма совместно-определённая. В этом сл-е Хn=b_n/C

Полученное зн-е Х_n подстав.в предпосл.ур-е,находим Х_n-1 и тд.,пока не получ.все неизв-е.

Обратный ход Гаусса. Из м-цы ступенч.вида записывается ур-е. Далее,начиная с конца находим все переменные. Допустим Х₄. Подставляем в верхнее и нах-м Х₃ и т.д.

Метод Гаусса — Жордана исп-ся для реш.квадр.систем лин.ур-ний, нахождения обрат.м-цы, отыскания ранга м-цы. Метод явл-ся модификацией метода Гаусса. Назван в честь Гаусса и Жордана.

Теорема Кронекера-Капелли. Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы.

r<m – ур-я с-мы(строки расш.м-цы)зависимые;

r=m –ур-я с-мы (стр.расш.м.)независимые;

r(A)не=r(A|B) - с-ма несовм-ная;

r(A)=r(A|B)=r – с-ма совм-ная;

r<n – с-ма неопред.(бескон.мн.реш.);

r=n – с-ма опред-ная (единств.реш.)

Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная.

Если система лин.ур-й имеет единств.решение Х=(х₁,х₂,…х_n),то такая сист.наз. определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист .не определённая.

8. Системы m линейных уравнений с n переменными.Теорема Кронекера-Капелли.Условие определённости и неопределённости любой системы линейных уравнений.

Системы m линейных уравнений с n переменными имеет вид:

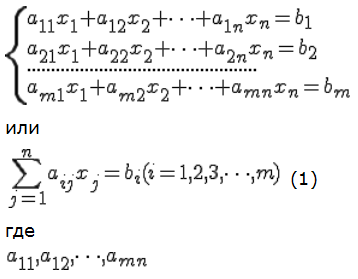
Произвольные числа, называемые соответственно коэффициентами при переменных и

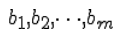
-свободными членами уравнений.
Решением системы (1) называется такая совокупность n чисел

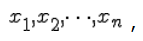
при подстановке которых каждое уравнение системы обращается в верное равенство

Теорема Кронекера-Капелли. Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы.

r<m – ур-я с-мы(строки расш.м-цы)зависимые;

r=m –ур-я с-мы (стр.расш.м.)независимые;

r(A)не=r(A|B) - с-ма несовм-ная;

r(A)=r(A|B)=r – с-ма совм-ная;

r<n – с-ма неопред.(бескон.мн.реш.);

r=n – с-ма опред-ная (единств.реш.)

Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная.

Если система лин.ур-й имеет единств.решение Х=(х₁,х₂,…х_n),то такая сист.наз. определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист .не определённая.

9. Базисные(основные) и свободные(неосновные) переменные системы m линейных уранений с n переменными. Базисное решение.
Любые m переменных системы m линейных уравнений с n переменными (m < n) называются основными, если определитель матрицы коэффициентов при них отличен от нуля. Тогда остальные m-n переменных называются неосновными (или свободными). Базисным решением системы m линейных уравнений c n переменными (m < n) называется всякое ее решение, в котором все неосновные переменные имеют нулевые значения.

10. Системы линейных однородных уравнений и её решения.Условия существования ненулевых решений системы.

Системы линейных однородных уравнений.

Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:

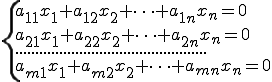
Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (или тривиальное) решение (0; 0;...; 0).

Систему (8) можно записать а виде:

А*Х=0 (9).

Если в системе (8) m=n, а ее определитель отличен от нуля, то такая система имеет только нулевое решение, как это следует из теоремы и формул Крамера. Ненулевые решения, следовательно, возможны лишь для таких систем линейных однородных уравнений, в которых число уравнений меньше числа переменных или при их равенстве, когда определитель системы равен нулю.

Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при r(A)<n.

11. Векторы на плоскости и в пространстве (геометрические векторы). Линейные операции над векторами(сложение,умножение вектора на число).Коллинеарные и компланарные векторы.
Вектором называется направленный отрезок, имеющий определенную длину, т. е. отрезок определенной длины, у которого одна из ограничивающих его точек принимается за начало, а вторая — за конец.

Если А — начало вектора и В — его конец, то вектор обозначается символом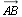

Обычно векторы обозначают одной малой латинской буквой со стрелкой либо выделяют жирным шрифтом: 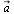, a.

Вектор изображается отрезком со стрелкой на конце:

Длина вектора 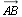называется его модулем и обозначается символом

Вектор 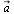, у которого 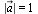называется единичным.

Вектор называется нулевым (обозначается ), если начало и конец его совпадают.

Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.

Векторы 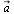и , расположенные на одной прямой или на параллельных прямых, называются коллинеарными. Нулевой вектор коллинеарен любому вектору.

Два вектора 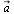и называются равными, если они коллинеарны, имеют одинаковую длину и одинаковое направление.

В этом случае пишут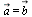

Все нулевые векторы считаются равными.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства (в частности, плоскости). Такой вектор называется свободным.

Два коллинеарных вектора (отличные от нулевых векторов), имеющие равные модули, но противоположно направленные, называются противоположными.

Вектор, противоположный вектору 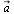, обозначается .

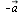Для 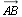вектора противоположным является вектор .

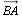Векторы a1, a2,..., an называются компланарными, если каждый из них параллелен одной и той же плоскости.

Любые два вектора всегда компланарны.

Очевидно, если три вектора компланарны, то их можно изобразить направленными отрезками, лежащими в одной плоскости.

Сумма векторов

Пусть даны два вектора а = OA(вектор) и b = OB(вектор) (рис. 5).

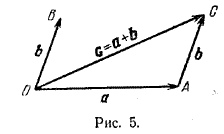
От точки А отложим отрезок АС такой, что AС(вектор) = b. Тогда, вектор с = OС(вектор) называется суммой векторов а и b и обозначается а + b.

Таким образом, OA(вектор) + AС(вектор) = OС(вектор). Это равенство называют правилом треугольника сложения двух векторов.

Oчевидно, что это правило справедливо и в том случае, когда точки О, А и В лежат на одной прямой (рис. 6, 7). В частности, а + 0 = а.

Не нашли, что искали? Воспользуйтесь поиском: