
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Приравнивая соотношения (1.7) и (2.5), получим
 (5.4)
(5.4)
Приравнивание формул (1.7) и (3.6) дает
(5.5)
 (5.6)
(5.6)
Для различных случаев сложных процентов получаем уравне-
ние эквивалентности, приравнивая формулы (3.1) и (3.6):
 (5.7)
(5.7)
 (5.8)
(5.8)
Полученная по формуле (5.7) годовая ставка сложных про-
центов, эквивалентная номинальной процентной ставке, называ-
ется эффективной ставкой сложных процентов.
Эффективную ставку сложных процентов полезно знать, чтобы
оценить реальную доходность финансовой операции, или срав-
нить процентные ставки в случае, когда используются различные
интервалы начисления. Очевидно, что значение эффективной
процентной ставки больше значения номинальной, а совпадают
они при т=1.
Далее из формул (3.1) и (4.1) имеем
(5.9)
 (5.10)
(5.10)
Аналогичным образом получаем зависимости между любыми
другими эквивалентными процентными ставками.
Проанализировав полученные формулы, можно
 сделать два замечания.
сделать два замечания.
1. Эквивалентность различных процентных ставок нико-
гда не зависит от величины первоначальной суммы р (для
данного рассматриваемого случая, когда первоначальная
сумма р предполагается одинаковой).
2. Эквивалентность процентных ставок всегда зависит от
продолжительности периода начисления за исключением
случая эквивалентности между собой сложных процентных
ставок разного вида (если период начисления один и тот
же).
Используя для вычислений формулы (3.1) и (4.1), можно по-
строить таблицу, отражающую зависимость между эквивалентны-
ми сложными учетными ставками и ставками ссудных процентов
(табл. 2). Видно, что небольшие учетные ставки имеют эквива-
лентные ставки ссудного процента, сопоставимые по величине,
но с ростом учетных ставок разница увеличивается очень быстро.
Таблица 2. Зависимость между эквивалентными сложными
учетными ставками dc(%) и ставками ссудных процентов ic(%)
| I dA%) | «%) | «%) | UK) |
| 5% | 5,26% | 50% | 100% I |
| 6% | 6,4% | 60% | 150% |
| 8% | 8,7% | 70% | 233% |
| 10% | 11% | 80% | 400% |
| 20% | 25% | 85% | 567% |
| 30% | 43% | 90% | 900% |
| 40% | 66,7% | 95% | 1900% |
| I 45% | 82% | 99% | 9900% | |
Можно определить также процентную ставку, эквивалентную
данной, когда начальные условия полностью или частично не со-
впадают. Данная ситуация может возникнуть, например, если
есть возможность выбора между различными коммерческими
предложениями.
Рассмотрим следующую задачу:
Какова должна быть сложная учетная ставка d0 чтобы сумма
Pj, вложенная под эту ставку на /ij лет, достигла той же величи-
ны, что и сумма P2, вложенная под сложную ставку ссудного про-
цента ic на Ai2 лет?
Поскольку финансовые результаты обеих операций должны
быть равны, составляем следующее уравнение эквивалентности:
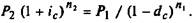
Отсюда
 (5.11)
(5.11)
Можно решить уравнение относительно /, тогда
 (5.12)
(5.12)
Аналогичные зависимости можно получать для любых видов
процентных ставок.
Принцип эквивалентности также используется при решении
вопросов финансовой эквивалентности платежей.
Как определить, что выгоднее, заплатить сумму ^1 через п^ лет
или сумму S2 через п2 лет? Будем считать, что Sx < S2 и пх < п2
(иначе задача имеет тривиальное решение).
В зависимости от размера процентной ставки (возьмем для
примера сложную ставку ссудного процента), под которую могут
быть вложены деньги, суммы ^1 и S2 имеют различные современ-
ные величины Р{и P2.

Очевидно, что для i = О S1 = P1 и S2= P2.
В этом случае выгоднее выплачивать меньшую сумму Sj. По-
скольку Л|< п2, для достаточно больших ic будет выполняться
Px > P2 (см. рис. 4). Тогда найдется /0, уравнивающая ставка, при
которой современные величины обеих сумм совпадут.
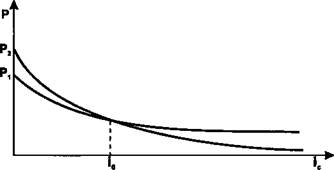
Рис. 4

Т.е.

|
откуда
(5.13)
Для всех ic < /0 предпочтительнее вариант с меньшей суммой и
меньшим сроком. Для /с > /0 —• с большими. При i = Z0 финансо-
вые результаты обеих операций эквивалентны.
Аналогичные формулы могут быть получены для всех видов
процентных ставок.
Пример 17
Срок уплаты по долговому обязательству — полгода, учетная
ставка равна 18%. Какова доходность данной операции, измерен-
ная в виде простой ставки ссудного процента?
Решение
Используем формулу (5.1):
I = 0,18/(1 - 0,5 • 0,18) = 0,198 = 19,8%.
Пример 18
Рассчитать эффективную ставку сложных процентов, если но-
минальная ставка равна 24% и начисление процентов происходит
ежемесячно.
Решение
Вычисление проводим по формуле (5.7):
ic = (1 + 0,24/12)12 - 1 = 0,268 = 26,8%.
Пример 19
Определить, под какую ставку процентов выгоднее поместить
капитал в 10 000 000 руб. на пять лет:
а) под простую ставку процентов 30% годовых;
б) под сложную ставку в 25% при ежеквартальном начислении?
Решение
В данном случае не обязательно считать величину наращенной
суммы, получаемой при различных процентных ставках. Поэтому
не важна величина первоначального капитала. Достаточно найти,
например, простую процентную ставку, эквивалентную данной
сложной ставке, воспользовавшись формулой (5.5):
I = [(I + 0,25/4)20 - 1] /5 = 0,472 =47,2%.
Так как простая процентная ставка (47,2%), которая дала бы
одинаковый с данной сложной процентной ставкой результат,
значительно превышает предложенную (30%), ясно, что гораздо
выгоднее использовать сложную процентную ставку. Посчитаем
теперь наращенные суммы, получаемые в обоих случаях, чтобы
выяснить, насколько более выгодна сложная ставка. Используем
для этого формулы (1.7) и (3.6):
а) S = 10 000 000 (1 + 5 • 0,3) = 25 000 000 (руб.).
б) S = 10 000 000 (1 + 0,25/4)20 = 33 618 521 (руб.).

|
Ощутимая разница в результатах подтверждает
сделанный ранее вывод. Можно заметить, что ре-
шение примера с использованием эквивалентных про-
центных ставок требует в два раза меньше вычислений.
Пример 20
Определить номинальную ставку процентов, которая обеспе-
чивала бы годовую доходность в 26%, если начисление процентов
происходит ежемесячно.
Решение
По формуле  (5.8) получаем
(5.8) получаем
Пример 21
Капитал, взятый в кредит, вложен под сложную ставку ссудно-
го процента 22% годовых. Для расчета с кредиторами необходимо
выплатить 30 000 000 через два года или 36 000 000 через три года.
Какой вариант предпочтителен?
"Решение
По формуле (5.13) найдем уравнивающую процентную ставку /0:
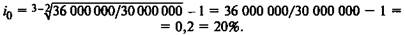
Данная нам ставка 22% больше найденной, следовательно, со-
временная величина второй (большей) суммы оказывается мень-
ше, предпочтительнее отдать ее через три года.
2.6. Учет инфляционного обесценения денег
в принятии финансовых решений
Инфляция характеризуется обесценением национальной валю-
ты (т. е. снижением ее покупательной способности) и общим по-
вышением цен в стране. Очевидно, что в различных случаях
влияние инфляционного процесса сказывается неодинаково.
Так, если кредитор (инвестор) теряет часть дохода за счет обесце-
нения денежных средств, то заемщик может получить возмож-
ность погасить задолженность деньгами сниженной покупатель-
ной способности.
Во избежание ошибок и потерь в условиях снижения покупа-
тельной способности денег рассмотрим механизм влияния ин-
фляции на результат финансовых операций и проведем неслож-
ные математические расчеты и преобразования.
Пусть Sa — сумма, покупательная способность которой с уче-
том инфляции равна покупательной способности суммы при от-
сутствии инфляции. Через AS обозначим разницу между этими
суммами.
Отношение AS /S9 выраженное в процентах, называется уров-
нем инфляции.
При расчетах используют относительную величину уровня ин-
фляции — темп инфляции а.

Тогда для определения Sa получаем следующее выражение:
 (6.1)
(6.1)
Величину (1 + а), показывающую, во сколько раз Sa больше S
(т. е. во сколько раз в среднем выросли цены), называют индексом
инфляции /и.
 (6.2)
(6.2)
Динамика индекса инфляции за несколько лет отражает изме-
нения, происходящие в инфляционных процессах. Понятно, что
повышение индекса инфляции за определенный период по срав-
нению с предыдущим таким же периодом указывает на ускорение
инфляции, снижение — на уменьшение ее темпов.
Пусть а — годовой уровень инфляции. Это значит, что через
год сумма S'a будет больше суммы S в (1 + а) раз. По прошествии
еще одного года сумма S^ будет больше суммы S'a в (1 + а) раз,
т. е. больше суммы Sb (1 + а)2 раз. Через п лет сумма S£ вырастет
по отношению к сумме 5в (1 + а)п раз. Отсюда видно, что инфля-
ционный рост суммы S при годовом уровне инфляции а — то же
самое, что наращение суммы S по сложной годовой ставке про-
центов а.
Разумеется, те же рассуждения применяются, если вместо года
берется любой другой временной интервал (квартал, месяц, день
и т. д.).
Очень важно запомнить данную аналогию со
 сложным процентом, так как одна из наиболее
сложным процентом, так как одна из наиболее
часто встречающихся ошибок, связанных с расчетом уров-
ня инфляции за некоторый период, связана именно с не-
учетом данного обстоятельства.
Например, если цены каждый месяц растут на 2%, то за
годовой уровень инфляции, недолго думая, принимают
2% • 12 = 24%. Такие расчеты часто используют банки и
финансовые компании, привлекая клиентов вкладывать
средства, к примеру, под 25% годовых. Между тем, если
уровень инфляции составляет 2% в месяц, это значит, что
за месяц цены вырастают в (1 + 0,02) = 1,02 раза, а за год —
в 1,0212 = 1,268 раза. Значит годовой темп инфляции со-
ставляет 1,268 - 1 = 0,268, т. е. годовой уровень инфляции
достигает 26,8%. После такого расчета процентная ставка
25% годовых теряет свою инвестиционную привлекатель-
ность и может рассматриваться лишь в плане минимиза-
ции потерь от инфляции.
По
Рассмотрим теперь различные случаи задания уровня инфля-
ции.
Если известен годовой уровень инфляции а, то за период в п
лет (при том, что п = па + пь и па — целое число лет, пь — остав-
шаяся нецелая часть года) индекс инфляции, очевидно, составит
следующую величину:
 (6.3)
(6.3)
В некоторых случаях может быть задан уровень инфляции ат
за короткий (меньше года) интервал. Тогда за период, составляю-
щий т таких интервалов, индекс инфляции будет равен
 (6.4)
(6.4)
Теперь можно приложить изложенные в предыдущих па-
раграфах варианты начисления процентов к условиям инфляци-
онной экономики.
Если в обычном случае первоначальная сумма P при заданной
ставке процентов превращается за определенный период в сумму
S, то в условиях инфляции она должна превратиться в сумму Sa,
что требует уже иной процентной ставки.
Назовем ее ставкой процентов, учитывающей инфляцию.
Пусть
— ставка ссудного процента, учитывающая инфляцию;
— учетная ставка, учитывающая инфляцию;
— номинальная ставка сложного процента, учитываю-
щая инфляцию;
— номинальная сложная учетная ставка, учитывающая
 инфляцию.
инфляцию.
Зададим годовой уровень инфляции а и простую годовую став-
ку ссудного процента /. Тогда для наращенной суммы S, превра-
щающейся в условиях инфляции в сумму Sa, используем формулу
(1-7): 
Для данной суммы можно записать еще одно соотношение:

а затем составить уравнение эквивалентности:

| ill |
из которого следует, что
 (6.5)
(6.5)
Мы получили, таким образом, известную формулу И. Фишера,
в которой сумма (а + /а) является величиной, которую необходи-
мо прибавить к реальной ставке доходности для компенсации ин-
фляционных потерь. Эта величина называется инфляционной
премией.
Зная формулу И. Фишера, можно избежать еще
 одной распространенной ошибки. Часто для под-
одной распространенной ошибки. Часто для под-
счета процентной ставки, учитывающей инфляцию, к вели-
чине реальной ставки доходности просто прибавляют ве-
личину темпа инфляции, т. е. если / = 25% и а = 15%, то за
процентную ставку, учитывающую инфляцию, принимается
сумма (/ + а) = 25 + 15 = 40%. Но нужно помнить, что суще-
ствует еще произведение (/ а), величина которого тем
больше, чем больше значения / и а. В нашем примере оно
составляет 0,15 • 0,25 = 0,0375 = 3,75%. Наверное не стоит
пренебрегать даже такой, на первый взгляд, небольшой
величиной. Ведь когда счет идет на десятки миллионов,
каждый процентный пункт — это сотни тысяч рублей.
Рассмотрим теперь различные случаи начисления процентов с
учетом инфляции. При этом всегда удобно пользоваться значени-
ем индекса инфляции за весь рассматриваемый период.
Для простых процентных ставок по формуле (1.7) получаем

В то же время должно выполняться равенство:
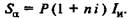
Составим уравнение эквивалентности:

из которого получаем
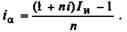 (6.6)
(6.6)
Для простых учетных ставок аналогичное уравнение эквива-
лентности будет иметь вид:
 (6.7)
(6.7)
Для случая сложных процентов используем формулу (3.1):

Отсюда
 (6.8)
(6.8)
Если начисление процентов происходит несколько (/и) раз в го-
ду, используем формулу (3.6):
Отсюда
 (6.9)
(6.9)
Таким же образом получаем две формулы для случая сложных
учетных ставок:
(6.10)
 (6.П)
(6.П)
Используя полученные формулы, можно находить процентную
ставку, компенсирующую потери от инфляции, когда заданы
процентная ставка, обеспечивающая желаемую доходность фи-
нансовой операции, и уровень инфляции в течение рассматри-
ваемого периода. Эти формулы можно преобразовать и получить
зависимость / от /а или любую другую. Например, из формулы
(6.6) можно получить формулу, позволяющую определить реаль-
ную доходность финансовой операции, когда задан уровень ин-
фляции и простая ставка процентов, учитывающая инфляцию:
 (6.12)
(6.12)
Из формулы (6.8) получаем аналогичную формулу для случая
сложных процентов:

|
(6.13)
Подставив в последнюю формулу вместо индекса инфляции
выражение  получим простую формулу:
получим простую формулу:
 (6.14)
(6.14)
отражающую несколько очевидных соображений:
Из
если ica = а (доходность вложений и уровень инфляции рав-
ны), то /с = 0, т. е. весь доход поглощается инфляцией;
если ica < а (доходность вложений ниже уровня инфляции), то
/с < 0, т. е. операция приносит убыток;
если /са > а (доходность вложений выше уровня инфляции), то
ic > 0, т. е. происходит реальный прирост вложенного капитала.
Пример 22
Кредит в размере 50 000 000 руб. выдан на два года. Реальная
доходность операции должна составить 10% годовых по сложной
ставке ссудного процента. Ожидаемый уровень инфляции состав-
ляет 15% в год. Определить множитель наращения, сложную став-
ку процентов, учитывающую инфляцию, и наращенную сумму.
Решение
По формуле (6.3) получаем
I11 = (I +0,15)2= 1,3225.
Множитель наращения и номинальная ставка доходности рав-
ны:
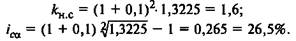
Далее для наращенной суммы получаем

Пример 23
Первоначальный капитал в размере 20 000 000 руб. выдается на
три года, проценты начисляются в конце каждого квартала по но-
минальной ставке 8% годовых. Определить номинальную ставку
процентов и наращенную сумму с учетом инфляции, если ожи-
даемый годовой уровень инфляции составляет 12%.
Решение
Воспользуемся формулой (6.3):
/и = (1 +0,12)3=1,4.
По формуле (6.9) имеем
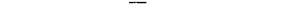
|
ja= [(I + 0,08/4) 1^M - 1] 4 = 0,107 = 10,7%.
Отсюда

|
S = 20 000 000 (1 + 0,107/4)12 = 27 454 048 (руб.).
Пример 24
При выдаче кредита должна быть обеспечена реальная доход-
ность операции, определяемая учетной ставкой 5% годовых. Кре-
дит выдается на полгода, за которые предполагаемый индекс ин-
фляции составит 1,06. Рассчитать значение учетной ставки, ком-
пенсирующей потери от инфляции.
Решение
Производим вычисления по формуле (6.7):

Пример 25
Определить реальную доходность финансовой операции, если
при уровне инфляции 0,9% в месяц выдается кредит на два года
по номинальной ставке сложных процентов 15% годовых. Про-
центы начисляются ежеквартально.
Решение
Принимая заданную номинальную процентную ставку за став-
ку, учитывающую инфляцию, получим из формулы (6.9) соотно-
шение для определения реальной номинальной ставки сложных
процентов:
 (6.15)
(6.15)
По формуле (6.4):

Отсюда

Пример 26
Определить, какой реальной убыточностью обладает финансо-
вая операция, если при уровне инфляции 14% в год капитал вкла-
дывается на один год под номинальную ставку 8% при еже-
месячном начислении.
Решение
Находим сначала индекс инфляции:

Далее используем формулу (6.15):

Таким образом, данная операция будет приносить 5,1%-ный
убыток.
Аннуитеты
В большинстве современных коммерческих операций подразу-
меваются не разовые платежи, а последовательность денежных
поступлений (или, наоборот, выплат) в течение определенного
периода. Это может быть серия доходов и расходов некоторого
предприятия, выплата задолженностей, регулярные или нерегу-
лярные взносы для создания разного рода фондов и т. д. Такая
последовательность называется потоком платежей.
Поток однонаправленных платежей с равными интервалами
между последовательными платежами в течение определенного
количества лет называется аннуитетом (финансовой рентой).
Теория аннуитетов является важнейшей частью финансовой
математики. Она применяется при рассмотрении вопросов до-
ходности ценных бумаг, в инвестиционном анализе и т. д. Наибо-
лее распространенные примеры аннуитета: регулярные взносы в
пенсионный фонд, погашение долгосрочного кредита, выплата
процентов по ценным бумагам.
Аннуитеты различаются между собой следующими основными
характеристиками:
• величиной каждого отдельного платежа;
• интервалом времени между двумя последовательными плате-
жами (периодом аннуитета);
• сроком от начала аннуитета до конца его последнего периода
(бывают и неограниченные по времени — вечные аннуитеты);
• процентной ставкой, применяемой при наращении или дис-
контировании платежей.
Аннуитет, для которого платежи осуществляются в начале со-
ответствующих интервалов, носит название аннуитета пренуме-
рандо; если же платежи осуществляются в конце интервалов, мы
получаем аннуитет постнумерандо (обыкновенный аннуитет) —
пожалуй, самый распространенный случай.
Наибольший интерес с практической точки зрения представ-
ляют аннуитеты, в которых все платежи равны между собой (по-
стоянные аннуитеты), либо изменяются в соответствии с некото-
рой закономерностью. Именно такие аннуитеты мы и изучим в
дальнейшем.
Введем следующие обозначения:
— величина каждого отдельного платежа;
— сложная процентная ставка, по которой начисляются
 проценты;
проценты;
— наращенная сумма для к-го платежа аннуитета постну-
мерандо;
— наращенная (будущая) сумма всего аннуитета постну-
мерандо (т. е. сумма всех платежей с процентами);
— современная величина fc-го платежа аннуитета постну-
мерандо;
— современная величина всего аннуитета постнумерандо
(т. е. сумма современных величин всех платежей);
— наращенная сумма аннуитета пренумерандо;
— современная величина аннуитета пренумерандо;
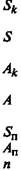 — число платежей.
— число платежей.
|
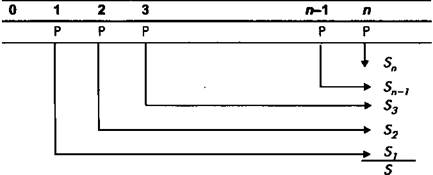
| Рис. 5. Будущая стоимость аннуитета постнумерандо |
Рассмотрим аннуитет постнумерандо с ежегодными платежами
P в течение п лет, на которые начисляются проценты по сложной
годовой ставке ic (рис. 5).
Сумма Si для первого платежа, проценты на который будут на-
числяться, очевидно, (п — 1) раз, составит по формуле (3.1):
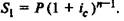
Для второго платежа (проценты на него будут начисляться на
один год меньше) имеем
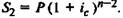
и так далее. На последний платеж, произведенный в конце л-го
года, проценты уже не начисляются, т. е.
Sn = P.
Не нашли, что искали? Воспользуйтесь поиском: