
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Так, для определения размера очередного платежа (7) имеем
(7.7)
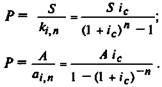 (7.8)
(7.8)
Для определения срока аннуитета (л), при прочих заданных ус-
ловиях, получаем
(7.9)
 (7.Ю)
(7.Ю)
Для конкретных вычислений выбирается одна из двух формул
каждой пары в зависимости от заданных известных величин.
Рассмотрим далее аннуитет пренумерандо с теми же начальны-
ми условиями (рис. 7).
Очевидно, отличие от предыдущего случая состоит здесь в том,
что период начисления процентов на каждый платеж увеличива-
ется на один год, т. е. каждая наращенная сумма Sk увеличивается
в (1 + /с) раз. Следовательно, для всей суммы Sn имеем

|
Рис. 7. Будущая стоимость аннуитета пренумерандо
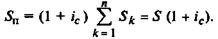
|
(7.11)
Для коэффициента наращения аннуитета пренумерандо kf1^
получаем следующее соотношение:
 (7.12)
(7.12)
Можно также заметить, что для определения современных зна-
чений каждого платежа дисконтирование по заданной ставке ic
проводится на один раз меньше, чем в случае аннуитета пренуме-
рандо. Поэтому каждая современная величина Ак будет больше в
(1 + /) раз. Таким образом,
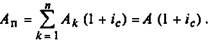 (7.13)
(7.13)
А для коэффициента приведения afn получаем
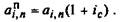 (7.14)
(7.14)
Для нахождения размера платежа и срока аннуитета пренуме-
рандо можно по формулам (7.11) и (7.13) найти для заданных зна-
чений Sn и An соответствующие значения 5 и А и пользоваться да-
лее формулами, выведенными для аннуитета постнумерандо.
Для определения коэффициентов наращения и
 приведения обыкновенного аннуитета существу-
приведения обыкновенного аннуитета существу-
ют таблицы, которыми удобно пользоваться в практиче-
ских вычислениях. Максимальные процентные ставки в та-
ких таблицах обычно не превышают 30—40%, что значи-
тельно ниже размера процентных ставок, применяемых в
России в настоящее время. Но нужно иметь в виду, что п в
данном случае — не число лет, а число периодов одинако-
вой продолжительности (день, месяц, квартал и т. д.), в ко-
торых принята данная процентная ставка. Таким образом,
если задана годовая процентная ставка, можно найти эк-
вивалентную ей ставку на более коротком интервале и
рассматривать далее п как число таких интервалов.
Если срок аннуитета п не ограничен, мы получаем случай веч-
ного аннуитета. Для аннуитета постнумерандо выражения для на-
ращенной суммы и современной величины приобретут следую-
щий вид:
(7.15)
 (7.16)
(7.16)
Для аннуитета пренумерандо, соответственно, получаем
(7.17)
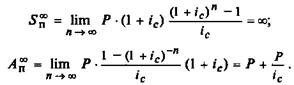 (7.18)
(7.18)
Таким образом, различие между двумя типами вечных аннуите-
тов, естественно, сказывается на определении их современной
величины.
Не менее важен случай, когда последовательность платежей из-
меняется по некоторому закону, и, следовательно, также может
быть описана с помощью математических средств.
Рассмотрим обыкновенный аннуитет, в котором платежи по-
стоянно увеличиваются на определенную положительную вели-
чину А, т. е. являются членами арифметической прогрессии с пер-
вым членом A1 = Ph разностью A. T. е. платежи представляют со-
бой ряд:
£/>+Л, />+2А,... Р+ (п- I)A.

|
Для наращенной суммы всего аннуитета получаем следующее
выражение:
Умножим обе части данного равенства на (1 + /с) и вычтем
первое выражение из полученного после умножения:
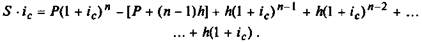
Видно, что часть полученного равенства представляет собой
сумму членов геометрической прогрессии, где A1 = A(I + Q; q =
= (1 + Q. После несложных преобразований получаем:
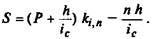 (7.19)
(7.19)
Найдем теперь современное значение аннуитета А.
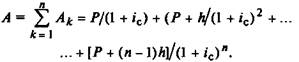
Умножим  обе части равенства на (1 + ir)n.
обе части равенства на (1 + ir)n.
Как видим, в данном случае верна формула (7.6), полученная
ранее для обыкновенного аннуитета:
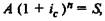
Отсюда
 (7.20)
(7.20)
Возможен также случай, когда платежи постоянно возрастают
в q раз, т. е. являются членами геометрической прогрессии:
P, Pq, Pq2,..., Pqn~X.
Тогда для наращенной суммы аннуитета имеем
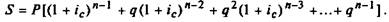
В квадратных скобках мы получили геометрическую прогрес-
сию с первым членом а\ = (1 + ic)n и знаменателем q/{\ + ic). Ис-
пользуя опять формулу для суммы геометрической прогрессии,
получаем выражение для S.
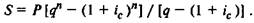
Очевидно, чтобы найти современное значение аннуитета А,
здесь также можно применить формулу (7.6):
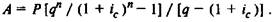
Теперь мы имеем возможность решить пример по определению
потока платежей произвольной величины.
Пример 27
Найти современную величину потока платежей, определяемого
следующим образом: первый год — поступления 500 ам. долл.,
второй год — поступления 200 ам. долл., третий год — выплата
400 ам. долл., далее в течение семи лет — доход по 500 ам. долл.
Ставка дисконтирования — 6% годовых.
Решение
В данном примере поток платежей в течение последних семи
лет представляет собой постоянный аннуитет. По формуле (7.5)
мы можем рассчитать его современную величину Aq. Нельзя за-
бывать, что это будет современная величина на момент начала
четвертого периода:
A0 = 500 • 5,58 = 2791 (ам. долл.)
(коэффициенты приведения находим по таблице 4 Приложе-
ния 2). Далее, используя формулу (3.11), находим современные
значения на момент начала потока платежа для всех оставшихся
платежей и величины A0:
А\ = 500 -0,953 = 471,5 (ам. долл.);
А2 = 200 • 0,89 = 178 (ам. долл.);
Аъ = -400 • 0,840 = -336 (ам. долл.);
А4 = 2791 • 0,840 = 2344,44 (ам. долл.).
Складывая получившиеся величины, находим современную ве-
личину всего потока платежей:
А = Ax + A2 + A3 + A4 = 2657,94 ам. долл.

Современная величина аннуитета
|
Во всех случаях, когда в произвольном потоке
платежей встречаются серии, которые могут быть
описаны как постоянные или изменяющиеся по некоторо-
му закону аннуитеты, следует обращать внимание на на-
чальный момент и срок этих аннуитетов, не совпадающие
с начальным моментом и сроком полного потока платежей.
Следующий этап нашего изучения — конверсия аннуитетов.
Под конверсией аннуитета понимается такое изменение на-
чальных параметров аннуитета, после которого новый аннуитет
был бы эквивалентен данному.
Два аннуитета считаются эквивалентными, если равны их со-
временные величины, приведенные к одному и тому же моменту
времени.
На практике необходимость рассчитать параметры эквивалент-
ного аннуитета чаще всего возникает при изменении условий вы-
платы долга, погашения кредита или займа и т. п. При этом кон-
версия может произойти как в момент начала аннуитета (на этот
момент и рассчитываются современные величины эквивалент-
ных аннуитетов), так и после выплаты некоторой части аннуите-
та. В последнем случае все расчеты производятся на остаток долга
в момент конверсии.
Рассмотрим наиболее распространенные случаи конверсии по-
стоянных аннуитетов.
1. Через некоторый промежуток времени л0 (он может быть ра-
вен и 0) после начала аннуитета весь остатрк долга может быть
выплачен за один раз (выкуп аннуитета). Очевидно, что в этом
случае величина выплачиваемой суммы будет равна современной
величине остатка аннуитета, рассчитанной для срока п\ = п- W0-
2. Может возникнуть задача, обратная предыдущей: задолжен-
ность погашается частями, в виде выплаты постоянного аннуите-
та, и требуется определить один из параметров аннуитета при за-
данных остальных. Поскольку здесь известна сумма долга, т. е.
современная величина аннуитета, для нахождения неизвестного
параметра используем формулы (7.8) или (7.10).
3. Период выплаты долга может быть изменен при сохранении
прежней процентной ставки. Величину P1 платежа для срока W1
находим, используя уравнения эквивалентности (приравнивают-
ся современные значения аннуитетов):
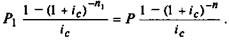
Отсюда
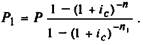
Очевидно, что, если срок аннуитета увеличится, значение P со-
кратится, и наоборот.
4. Может возникнуть ситуация, когда величина платежа P дол-
жна быть изменена в ту или другую сторону. Рассмотрим данный
случай на примере 28.
Пример 28
Для погашения кредита, выданного под сложную процентную
ставку 4% годовых, в течение 10 лет должны вноситься ежегодные
платежи в размере 5 000 ам. долл. Изменившиеся условия дают
возможность с самого начала вносить по 7 500 ам. долл. Опреде-
лить новый срок W1, за который долг будет полностью выплачен.
Решение
Рассчитаем сначала современную величину имеющегося анну-
итета (которая и представляет собой величину долга на началь-
ный период).
По формуле (7.5) получаем
А = 5 000 [1 - (1 + 0,04)-10]/0,04 = 40554,5 (ам. долл.).
Далее для изменившегося P найдем коэффициент приведения
аннуитета по той же формуле:
ain = AfPx = 40554,5 ам. долл./ 7500 ам. долл. = 5,4.
Используя таблицу 4 Приложения 2 найдем значение W1, более
всего подходящее данному коэффициенту при процентной ставке
4%, округляя его в меньшую сторону: W1 = 6. Поскольку значение
W1 найдено приближенно, необходимо рассчитать современное
значение нового аннуитета:
Ax = 7 500 [1 - (1 + 6,04)"6]/0,04 = 39 316 (ам. долл.).
Если величины платежей изменяться не могут, недостающая
сумма Aq = 40 554,5 — 39 316 = 1238,5 (ам. долл.) должна быть вы-
плачена кредитору сразу. (Пример, когда в такой ситуации кор-
ректируются величины платежей, рассматривается в конце этого
раздела).
5. Начало выплаты задолженности при заданной процентной
ставке гс может быть отсрочено:
а) при сохранении размера платежа;
б) при сохранении срока выплаты.
Очевидно, что в первом случае должен увеличиться срок ан-
нуитета, а во втором — величина платежа.
Обозначим через W0 период отсрочки. Тогда на момент начала
выплаты, сумма долга Ax, которая должна являться современной
величиной нового аннуитета, составит по формуле сложного про-
цента:
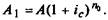
Отсюда получаем уравнение эквивалентности:
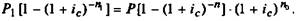
Далее поступаем аналогично рассмотренным ранее случаям. В
первом варианте находим значение п± продолжительности нового
аннуитета при заданном значении P1 = Р(п{ будет найдено при-
ближенно, поэтому потребуется выплата компенсирующей сум-
мы, см. пример 28). Во втором — величину платежа P1 при Ai1 =
= п - Ai0.
6. В некоторых случаях может потребоваться объединение не-
скольких аннуитетов в один (консолидация аннуитетов). При
этом объединяемые аннуитеты могут быть любыми, а в искомом
объединяющем аннуитете один из параметров неизвестен при
всех остальных заданных.
Пример 29
Два аннуитета с параметрами:
1) величина платежа —- 2 000 ам. долл., процентная ставка —
5% годовых, срок — 12 лет;
2) величина платежа — 3 500 ам. долл., процентная ставка —
6% годовых, срок — 10 лет;
требуется заменить одним — со сроком 10 лет и процентной став-
кой 6% годовых.
Определить величину нового платежа.
Решение
Найдем сначала общую современную величину двух аннуите-
тов. По формуле (7.5) имеем
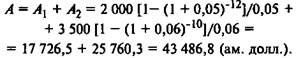
Далее по формуле (7.7) находим величину нового платежа:
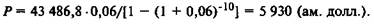
Нам остается теперь рассмотреть важное практическое прило-
жение теории аннуитетов — составление различных вариантов
(планов) погашения задолженности. При составлении плана по-
гашения интерес представляют размеры периодических платежей
заемщика — выплаты процентов и выплаты по погашению ос-
новной суммы долга — при различных условиях погашения (та-
кие платежи носят название срочных уплат).
Основных вариантов погашения задолженности — пять:
1. Займы без обязательного погашения, по которым постоянно
выплачиваются проценты. Задача в данном случае заключается в
нахождении размера выплачиваемой суммы P при заданной про-
центной ставке /. Мы имеем здесь случай вечного аннуитета. Раз-
мер платежа определяется по формуле (7.15), из которой получаем
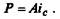
Не нашли, что искали? Воспользуйтесь поиском: