Движение электрона в атоме

Электрон в атоме не может быть непод­вижным, так как под действием силы электростатического притяжения он немедленно упал бы на положи­тельно заряженное ядро. Но электрон и не вращается вокруг атомного ядра.

Согласно современным представлениям электрон имеет двойствен­ную природу[29], проявляя одновременно свойства частицы[30] (вещества) и электромагнитной волны[31] (поля).

Наличие массы и заряда характеризует электрон как частицу, а способность электрона подвергаться дифракции и интерференции [32] свидетельствует о его волновых свойствах.

Особенности поведения электрона в атоме вызваны прежде всего его волновыми свойствами, так как движение волны принципиально отличается от движения частицы. При описании движения волны нельзя пользоваться понятием "траектория". Поэтому для характеристики движения электрона вместо терминов "траектория" и "орбита", опираясь на законы квантовой (волновой) механики[33], применяют вероятно­стный подход.

Квантовая механика показала, что электрон движется по всему атомному объё­му, образуя электронное облако, которое для разных электронов может иметь разную форму (рис. 17). При этом частота пребывания электрона (плотность электронного облака) в той или иной области атомного пространства неодинакова (рис. 13), то есть движение электрона в атоме носит вероятностно-волновой характер.

Таким образом, движение электрона описывают через веро­ятность его нахождения в данной точке атомного про­странства. В одних областях такого пространства электрон можно обнаружить чаще (и говорят о большей вероятности его нахождения в них), в других – реже (меньшая ве­роятность пребывания его там), в третьих он не бывает никогда (тогда говорят о нулевой вероят­ности). Соответственно говорят о повышенной или пониженной электронной плотности в разных областях атомного пространства; вблизи атомного ядра она практически равна нулю.

Согласно законам квантовой механики электрон в силу высокой скорости движения в атоме (2·10⁶ м/с, или 2000 км/с) оказывается как бы находящимся одновременно во всём его объёме кроме ядра, образуя электронное облако1 с неравномерной плотностью, которое у электронов одного и того же атома может иметь разную форму. Формы электронных облаков аналогичны атомным орбиталям [34].

Атомной орбиталью (АО) называется пространство вокруг атомного ядра, в котором наиболее вероятно пребы­вание электрона с определённой энергией; обычно такая вероятность принимается равной 90 %.

Например, для атома во­дорода на расстоянии более 120 пм от ядра вероятность пребывания электрона становится настолько малой, что ею можно пренебречь. И, очер­тив вокруг атомного ядра сферу радиусом 120 пм, можно сказать: "Вот область пространства, где движется электрон в атоме водорода".

Атомная орбиталь характеризуется энергией, размерами, формой и ориентацией в пространстве относительно ядра атома.

Для уточнения понятия "орбиталь" приведём такую ана­логию. Допустим, имеется множество фотографий одного из участников футбольного матча, например вратаря. Используя эти фотографии, можно нанести на чертёж все точки футбольного поля, где во время матча в разные моменты застал вратаря объектив фотографа. Ясно, что наибольшее число отметок придётся на участки поля, непосредственно примыкающие к воротам, – там вратарь бывает чаще, поэтому там больше и вероятность его обнаружения. Полученное таким способом "вратарное облако", конечно, не будет обра­зом самого вратаря, а будет характеризовать его движение по футбольному полю во время матча.

Изменение вероятности нахождения электрона на каком-либо удалении от атомного ядра можно изобразить при помощи графика. Но такой способ недостаточно нагляден, поэтому принято изображать вероятность нахождения электрона при помощи точек: чем больше вероятность нахождения электрона в той или иной области атомного пространства, тем больше плотность точек. Именно таким образом на рис. 13 изображено электронное облако атома водорода.

Рис. 13. Электронное облако и граница атомной орбитали

в атоме водорода

Причём точки на рисунке нельзя отождествлять с электроном. Не корректным будет и утверждение, что электрон "размазан в пространстве" – просто невозможно знать, где именно в данный момент времени он находится. Рядом с атомным ядром, а также на значительном удалении от него вероятность нахождения электрона мала, но не равна нулю. Расстояние от атомного ядра, на котором вероятность нахождения электрона наиболее высока, принято называть атомным радиусом. Так, например, радиус атома водорода равен 78 пм.

Граничная поверхность атомной орбитали характеризуется изоэлектронной плотностью, то есть она является поверхностью, равной электронной плотности. Все атомные орбитали изображаются трёхмерными фигурами. Возникновение, например, p-орбиталей можно представить вращением их двумерных изображений на 180⁰ вокруг соответствующих осей декартовой системы координат этих осей. Орбитали и 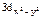располагаются вдоль, а 3d_xy , 3d_yz и 3d_xz – между этими осями (см. рис. 17).

Графически атомную орбиталь принято изображать в виде квантовой (энергетической) ячейки в форме круга ○, черты — или квадрата (клетки) □, а электроны – в виде стрелок, направленных вверх или вниз: – спаренные электроны; – неспаренный электрон; свободная, или вакантная, орбиталь – □.

Вследствие закономерностей дви­жения электронной волны в ограниченном пространстве круговой ("боровской", см. с. 15) орбиты возникает так называемая трёхмерная стоячая волна, наглядной моделью которой является механическая одномерная стоячая волна колеблющейся струны, то есть на длине орбиты укладывается целое число волн (рис. 14).

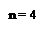
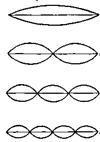
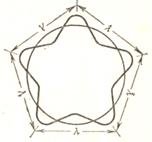
а б

Рис. 14. Стоячие волны (а) в колеблющейся струне

и (б) электронная волна в пределах атома (n = 5)

Отсюда вытекают закономерности математического описания волновых свойств элек­трона в атоме, который может находиться не в любых, а только в оп­ределённых состояниях, то есть для состояний электрона в атоме и величин, их характеризующих, свойственна квантованность (дискретностность).

Аналогией может служить человек, совершающий серию прыжков с пола – на стул, со стула – на стол и обратно. При известной сноровке он может запрыгнуть с пола сразу на стол, но никакая физическая подготовка не позволит ему оказаться где-нибудь в промежутке между поверхностями (пол – стул – стол). Нечто подобное происходит и в атоме: энергия электрона может принимать только определённые значения.

Квантовые числа

Основная характеристика, определяющая состояние электро­на в поле атомного ядра, – его энергия, которая принимает лишь определённые квантованные значе­ния.Атомная орбиталь, как любая геометрическая фигура, характеризуется тре­мя параметрами (координатами). Электронное облако характеризу­ется четырьмя параметрами, так как электрон в атоме участвует в двух видах движения: орбитальном относительно ядра и собст­венном вращательном. Следо­вательно, для полной характеристики состояния электрона в ато­ме необходимо иметь четыре параметра:

• энергию электрона		характеризуют движение электрона в атоме вокруг ядра
• величину орбитального момента количества движения электрона
• направление орбитального момента количества движения электрона
• направление собственного момента количества движения электрона		характеризует собственное (как бы вращательное) движение электрона

Эти параметры вследствие волновых свойств электро­на, также как и его энергия, принимают определённые значения, то есть их величины пропорциональны безразмерным величинам, называемым квантовыми числами.

Главное квантовое число (n) характеризует энергию электрона в атоме водорода и общий запас энергии электрона в любом многоэлектронном атоме, то есть энергетический уровень атома. Это число определяет и размеры атомной орбитали. Чем большей энергией обладает электрон, тем менее прочно он связан с атомным ядром.

Главное квантовое число может принимать значения натуральных чисел от единицы до бесконечности: n = 1, 2, 3,… ∞. Число энергетических уровней атома в основном состоянии равно номеру периода в периодической системе химических элементов, в котором находится данный элемент. Поэтому для электронов атома n изменяется от 1 до 7 (соответственно номеру периода в периодической системе химических элементов). Энергетические уровни обозначаются арабскими цифрами, соответствующими значению n или латинскими буквами K-, L-, М-, N-, O-, P-, Q и т.д. При п = 1 электрон находится на первом (или К-энергетическом) уровне, то есть в состоянии с минимальной энергией. По мере возрастания п энергия уровней, которая имеет отрицательные значения, увеличивается. При n → ∞ энергия притяжения электрона атомным ядром стремится к нулю. Электрон отрывается от атома, и происходит его ионизация:

Э – е^– → Э⁺.

Физический смысл главного квантового числа иллюстрирует рис. 14а, на котором указано, что число стоячих волн однозначно определяется значением n. Поскольку электронные волны в атоме представляют собой более сложный процесс, чем стоячая волна колеблющейся струны, состояние электрона определяется не одним, а четырьмя квантовыми числами.

На рис. 15 представлена диаграмма1, на которой положение каждого энергетического уровня атома отображается горизонтальной чертой. Разность энергий между первым и вторым уровнями относительно велика. Однако она резко уменьшается между каждым последующими энергетическими уровнями, так как с увеличением заряда атомного ядра усиливается притяжение между этим ядром и электронами, что сопровождается уменьшением размера атома.

Помимо энергии главное квантовое число определяет размеры атомной орбитали. Чем больше значение n, тем больше энергия электрона, и тем дальше от атомного ядра располагается область его наиболее вероятного нахождения, и, следовательно, больше радиус (r) атома:

E ₁ < Е ₂ < E ₃ <... < E_n; r ₁ < r ₂ < r ₃ <... < r_n .

+ Е
0	––– n → ∞
	––– n = 4
	––– n = 3
	–––n = 2
– Е	–––n = 1

Рис. 15. Диаграмма энергетических уровней атома

Значение главного квантового числа ука­зывает также на число подуровней на энергетическом уровне. Так, например, первый энергетический уровень (n = 1) состоит из одного подуровня, второй (n = 2) – из двух, третий (n = 3) – из трёх и т. д.[35]

Таким образом, главное квантовое число характеризует энергетический уровень атома и среднее расстояние, на которое электрон этого уровня удалён от атомного ядра, обозначает номер энергетического уровня и определяет в нём число подуровней, а также соответствует номеру периода в Периодической системе химических элементов Д.И. Менделеева (табл. 2).

Орбитальное (побочное, азимутальное) квантовое число ( l) характеризует момент количества движения (момент импульса) электрона вокруг атомного ядра[36]. Иными словами, оно уточняет энергетическое состояние электрона в атоме в пределах энергетического подуровня. Значения l задаются для каждого энергетического уровня главным квантовым числом. Для электронов, находящихся на энергетическом уровне со значением п, l может принимать значения натуральных чисел от 0 до n – 1. Это значит, что количество возможных значений l (число энергетических подуровней) равно значению n (табл. 2), но фактически, ни один уровень не имеет больше четырёх подуровней.

Энергия электронов, характеризуемых одинаковыми значениями n, но разными значениями l, неодинакова, так как они занимают разные атомные орбитали. Совокупности электронов с одинаковыми значениями l образуют энергетические подуровни, которые обозначаются буквами: s, p, d, f (и далее по алфавиту). Энергетические подуровни, характеризующиеся значениями l: 0, 1, 2, 3, называют соответственно s -, p -, d -, f -подуровнями[37], а находящиеся на них электроны s -, p -, d -, f -электронами.

Пер­вый энергетический уровень (n = 1, l = 0) состоит из одного s -подуровня; второй (n = 2), третий (n = 3) и четвёртый (n = 4) энергети- че­ские уровни состоят соответственно из двух (s, р), трёх (s, p, d) и четырёх (s, p, d, f) подуровней. Больше четырёх подуровней не заполняется, так как значения l: 0, 1, 2, 3 характеризуют энергию электронов всех 118 известных в настоящее время химических элементов. Значения l определяет также формы атомных орбиталей (электронных облаков):

- при l = 0 энергетическому s -подуровню соответствует орбиталь сферической формы, называемая s-орбиталью (рис. 17);

- при l = 1 р -подуровень содержит три орбитали в форме объёмной восьмёрки (гантели), называемые р -орбиталями (рис. 17);

- при l = 2 d -подуровень содержит пять d -орбиталей, четыре из которых имеют форму двух взаимно перпендикулярных объёмных восьмёрок, а одна – объёмную восьмерку, находящуюся в торе (рис. 17);

- при l = 3 f- под­уровень содержит семь f -орбиталей сложной формы (рис. 17).

Энергетические подуровни принято обозначать двумя символами: цифровым (главное квантовое число) и буквенным (орбитальное квантовое число), например: 1 s, 2 s, 2 p, 3 d, 4 f.

В многоэлектронном атоме, вследствие межэлектронных взаимодействий, в пределах одного энергетического уровня вели­чины энергии подуровней различны, причём Е_ns < Е_пр < E_nd < E_nf.

Таким образом, орбитальное квантовое число характеризует тип и энергию подуровня, а также определяет форму атомной орбитали (табл. 2).

Магнитное квантовое число (m_l) характеризует проекцию орбитального момента количества движения (момента импульса) электрона, который как величина векторная может совпадать с направлением внешнего электрического или магнитного поля, иметь противоположное направление или принимать промежуточные значения. Количество положений этого вектора, а следовательно, и проекций его на произвольно выбранную ось, обычно совмещаемую с направлением внешнего поля, определяется значением m_l (рис. 16).

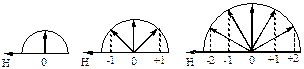
Рис. 16. Ориентации орбитального момента количества движения электрона относительно направления внешнего магнитного поля

Иными словами, магнитное квантовое число связано с магнитным моментом электрона, обусловленным его орбитальным движением как заряженной частицы в электрическом или магнитном поле, и характеризует ориентацию атомных орбиталей относительно направления этого поля.

Магнитное квантовое число принимает целочисленные значения от – l до +l, включая нуль, то есть 2 l + 1 значений, которым соответствует число атомных орбиталей на данном энергетическом подуровне.

Следует отличать количество значений, которое может принимать магнитное квантовое число при данном l, от самих его зна­чений. Количество значений m_l – это число энергетических состояний (атомных орбиталей), в которых могут находиться электроны данного энергетического подуровня. При определённых n и l может быть несколько состояний электрона с одинаковой энергией. Эти состояния называются вырожденными. Так, для s -электронов возможно лишь одно состояние (2 · 0 + 1 = 1), для р -электронов – 3 со­стояния (2 · 1 + 1 = 3), для d - и f -электронов – соответственно 5 и 7 состояний (рис. 17), то есть s -, p -, d -, f -электроны вырождены однократно, троекратно, пяти- и семикратно.

Таким образом, m_l определяет число атомных орбиталей на энергетическом подуровне и их ориентацию в пространстве (табл. 2).

s -орбиталь (l = 0)

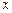
m_l = 0

p -орбитали ( l = 1)

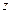
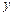
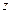
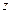
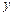
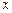
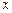
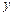
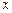
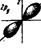
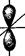
p_y (m_l = -1) p_z (m_l = 0) p_x (m_l = +1)

d -орбитали ( l = 2)

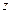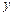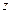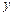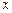
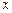
d_xy (m_l = -2) d_yz (m_l = -1) d_z² (m_l = 0) d_xz (m_l = +1) d_x² _{– y}² (m_l = +2)

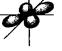
f -орбитали (l = 3)

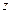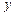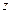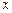
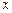
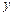
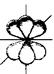
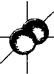
(m₁ = -3, -2, -1, 0, +1, +2, +3)

Рис. 17. Формы атомных орбиталей

При помощи трёх квантовых чисел п, l и m_l описывается состояние электрона при перемещении его в пространстве с тремя степенями свободы относительно атомного ядра, то есть характеризуется атомная орбиталь, на которой находится данный электрон.

Вместе с тем электрон, обладая собственным моментом количества движения (моментом импульса), как электрически заряженная частица, имеет и собственный магнитный момент – спин.

Спиновое квантовое число (т_s), или просто спин (S), характеризует собственный момент количества движения (момент импульса) электрона.

Спиновое квантовое число может принимать только два зна­чения: +½ и –½, в зависимости от того, параллельно или антипараллельно внешнему магнитному полю, ориентируется магнитное поле электрона, обусловленное собственным движением электрона.

Спин электрона – это внутренняя его характеристика, как масса или электрический заряд, четвёртая степень его свободы, имеющая сугубо квантовый характер. При переходе к классической механике спин обращается в нуль, и в этом смысле классического аналога не имеет.

 

Наличие у атомов спина в 1922 году подтвердили экспериментально немецкие физики Отто Штерн и Вальтер Герлах. Исследуемое вещество (серебро) разогревалось в специальной печи П до парообразного состояния (рис. 18). Пучок атомов, выделенный с помощью диафрагмы D, направлялся между полюсными наконечниками, создающими неоднородное магнитное поле. Движение атомов происходило в вакууме и заканчивалось на стеклянной пластинке С (экран). Пучок атомов с точки зрения классических представлений должен был создать на экране сплошное размытое изображение, так как магнитный момент атомов может принимать любые значения. Согласно же квантовой теории, оперировавшей лишь орбитальным магнитным моментом, пучок атомов должен был либо расщепиться, по меньшей мере, на три части, либо остаться неизменным. Однако эксперимент показал, что пучок атомов одновалентных элементов делится на две одинаковые части, свидетельствуя о том, что магнитный момент атомов принимает не любые значения. Для объяснения этого эффекта американские физики Джордж Уленбек и Сэмюэл Абрахам Гаудсмит в 1925 г. выдвинули гипотезу о существовании у электрона собственного магнитного момента – спина, предположив, что электрон можно рассматривать как "вращающийся волчок" (отсюда и термин "спин", от англ. spin – вращение).

Выполненные позже опыты с пучками атомов других металлов, а также с пучками протонов и электронов доказали существование собственного магнитного момента у всех исследованных частиц, что явилось доказательством постулатов квантовой теории.

 

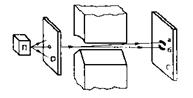
Рис. 18. Схема опыта Штерна-Герлаха

Значения спинового квантового числа +½ и –½ символически обозначают противоположно направленными стрелками ↑ и ↓. Электроны, находящиеся на одной атомной орбитали и имеющие одинаковые значения квантовых чисел n, l, m_l, но противоположно направленные (антипараллельные) спины: ↑↓, называются спаренными или неподелённой электронной парой. Электроны с нескомпенсированными параллельными спинами: ↑↑ называются неспаренными.

 

 

Таким образом, значения спинового квантового числа определяют проекции собственного магнитного момента электрона на ось квантования (рис. 19, табл. 2).

 

 

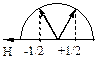
Рис. 19. Ориентации спинового момента электрона

относительно внешнего магнитного поля

 

С целью наглядной иллюстрации понятия "спин" электрон уподобляют заряженному шарику, движущемуся вокруг своей оси по часовой или против часовой стрелки (рис. 20). Однако это крайне грубая аналогия, ибо электрон даже отдалённо не напоминает шарик. Представить же наглядно, что электрон как волна "крутится волчком", невозможно.

 

ms = –1/2

ms = +1/2

ms = –1/2

 

Рис. 20. Модель орбитального и внутреннего движения электронов

как частиц в атоме лития

Таким образом, квантовые числа n, l, m_l определяют форму, размеры и ориентацию в пространстве атомных орбиталей (табл. 2).

 

Таблица 2

Квантовые числа

 

⇐ Предыдущая234567891011Следующая ⇒

---

Не нашли, что искали? Воспользуйтесь поиском: