Полная производная по времени t функции Ляпунова, вычисленная в силу системы

Пусть дана нелинейная нестационарная система дифференциальных уравнений вида:

(1.6.1)

с областью определения

(1.6.2)

Причем в этой области функция :

(а)) непрерывна по t, x;

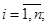
(б) имеет непрерывные частные производные вида , (1.6.3) ограниченные равномерно по на любом компактном подмно-

жестве из области (или говорят кратко, непрерывно

дифференцируемы по );

в) 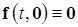, т.е. система допускает тривиальное решение

Повторим, что условия (1.6.3) означают, что область (1.6.2) есть область единственности для системы (1.6.1).

Пусть также дана функция Ляпунова вида , определенная в некоторой области , и пусть функция Ляпунова вида – непрерывно дифференцируема по t, x в 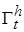, т.е. усилим свойства ее непрерывности, задаваемые введенным выше определением функции Ляпунова.

Вычислим полную производную по времени как сложную функцию аргументов t, x. Введем обозначения

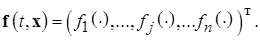
Тогда

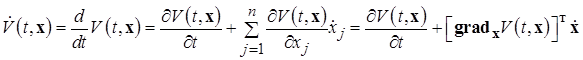
Подставляя в последнее выражение для 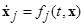в силу системы (1.6.1), получим:

(1.6.4)

Здесь введена вектор-функция – градиент скалярной-функции по вектору x вида:

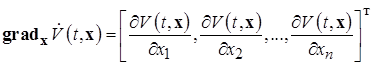(1.6.5)

Определение. Выражение (1.6.4) называется полной производной по времени t функции Ляпунова , вычисленной в силу приведенной системы (1.6.1).■

Замечание 1. Если 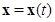есть произвольное решение системы (1.6.1), то , в силу выражения (1.6.4), представляет собой полную производную по времени t сложной функции , т.е.

.■ (1.6.6)

Замечание 2. Заметим, что если функции Ляпунова из формулы полной производной (1.6.4) не придать дополнительные свойства непрерывной дифференцируемости по t и x, то из формулы (1.6.6) могут не следовать формулы (1.6.4), (1.6.5), так как для ) не будет удовлетворяться требование непрерывности по t, x кней как к функции Ляпунова. ■

Не нашли, что искали? Воспользуйтесь поиском: