Способы задания плоскости на чертеже

Всякая геометрическая фигура, погруженная в пространство, состоит из некоторого множества точек пространства. Плоскость как одна из геометрических фигур, представляет собой совокупность множества точек. Из этого определения плоскости можно установить способы задания ее положения в пространстве. Для этого достаточно вспомнить аксиому сочетания – через три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну.

На рис. 21 представлены способы задания положения плоскости в пространстве:

а – тремя точками, не лежащими на одной прямой;

б – прямой и точкой, взятой вне прямой;

в – двумя пересекающимися прямыми;

г – двумя параллельными прямыми.

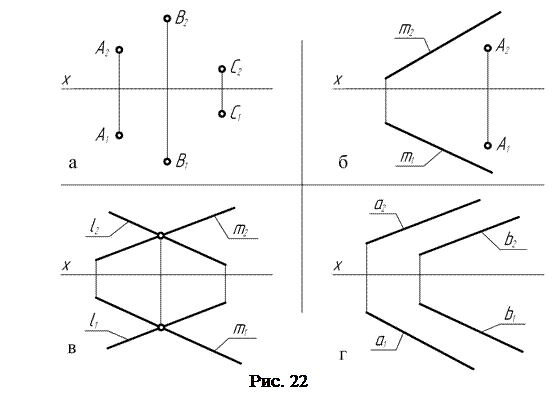
На комплексном чертеже (рис. 22) плоскость может быть задана:

а – проекциями трех точек, не лежащих на одной прямой;

б – проекциями прямой и точки, взятой вне прямой;

в – проекциями двух пересекающихся прямых;

г – проекциями двух параллельных прямых.

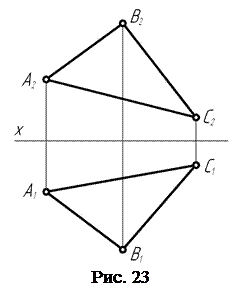
Каждый из представленных на рис. 22 способов задания плоскости на чертеже может быть преобразован из одного в другой. Так, например, проведя через точки А и В (рис. 22, а) прямую, получают задание плоскости, представленное на рис. 22, б. От него можно перейти к способу, представленному на рис. 22, г, если через точку С провести прямую, параллельную прямой АВ. Если точки А, В и С соединить попарно прямыми, то получают треугольник АВС – плоскую фигуру (рис. 23), проекциями которой может быть задана плоскость на чертеже.

При этом всегда следует помнить о том, что плоскость, как геометрическая фигура, безгранична и поэтому нельзя ограничиваться построениями только в пределах площади этого треугольника, так как в общем случае проекции плоскости занимают всю каждую из плоскостей проекций: горизонтальную П_I, фронтальную П₂ и профильную П₃.

Более наглядно плоскость может быть задана при помощи прямых, по которым она пересекает плоскости проекций (рис. 24, а).

Эти прямые называются следами плоскости. В общем случае оба следа должны пересекаться между собой в точке на оси проекций, которую называют «точкой схода следов».

Из всего многообразия положений плоскости относительно заданной системы плоскостей проекций обычно выделяют такие, когда:

- плоскость перпендикулярна одной из плоскостей проекций;

- плоскость параллельна одной из плоскостей проекций;

- плоскость не перпендикулярна и не параллельна ни одной из плоскостей проекций.

Не нашли, что искали? Воспользуйтесь поиском: