Принадлежность прямой и точки плоскости

Известно, что принадлежность прямой линии плоскости устанавливает аксиома сочетания – если две точки прямой располагаются непосредственно на плоскости, то и сама прямая принадлежит этой плоскости. На основании принадлежности точки прямой можно сформулировать и признак принадлежности точки плоскости – если точка принадлежит плоскости, то она должна принадлежать прямой, лежащей в этой плоскости.

С помощью признаков принадлежности прямой и точки плоскости успешно решаются многие метрические и позиционные задачи начертательной геометрии. Так, при рассмотрении вопроса о принадлежности точки М (рис. 36, а) плоскости общего положения, заданной треугольником АВС, исходят из того, что точка М будет принадлежать плоскости только в том случае, если она располагается непосредственно на прямой, принадлежащей этой плоскости. Отсюда следует план решения задачи – провести через тоску М прямую, принадлежащую плоскости треугольника АВС. Если это условие выполнимо, тогда точка М будет принадлежать плоскости.

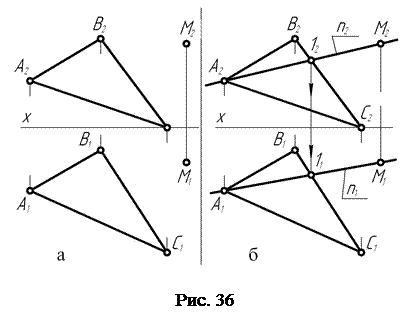На чертеже (рис. 36, б) необходимые условия выполняют в следующей последовательности: на горизонтальной или фронтальной плоскости проекций через соответствующую проекцию точки М проводят произвольную прямую таким образом, чтобы она проходила через две точки, заведомо принадлежащие плоскости треугольника АВС.

Например, на фронтальной плоскости проекций через точку М₂ проведена произвольная прямая n₂ так, что она проходит через точки А₂ и I₂, определяющие принадлежность прямой n заданной плоскости. Затем с помощью точек I₁ и А₁ построена горизонтальная n₁ проекция прямой, принадлежащей плоскости.

В результате выполненных построений оказалось, что проекции точки М (М₂, М₁) располагаются на соответствующих проекциях прямой n (n ₂, n ₁), принадлежащей плоскости треугольника АВС. На основании этого можно сделать вывод о том, что точка М принадлежит заданной плоскости. В случае несовпадения расположения проекций точки М на соответствующих проекциях прямой n, принадлежащей плоскости, следовало бы сделать вывод о том, что точка М плоскости треугольника АВС не принадлежит.

Среди множества прямых, принадлежащих плоскости, наибольший практический интерес представляет построение прямых наибольшего наклона плоскости к той или иной плоскости проекций.

Прямые линии, расположенные перпендикулярно прямым уровня плоскости, называются прямыми наибольшего наклона плоскости к плоскостям проекций.

Не нашли, что искали? Воспользуйтесь поиском: