Перпендикулярность прямой плоскости

Прямая линия в пространстве может располагаться перпендикулярно плоскости. Положение же плоскости в пространстве однозначно определяется положением двух пересекающихся прямых, принадлежащих этой плоскости. Таким образом, в случае перпендикулярности прямой плоскости она должна располагаться перпендикулярно двум пересекающимся прямым, лежащим в этой плоскости. С другой стороны, прямой угол между пересекающимися прямыми проецируется в натуральную величину только в том случае, когда одна из его сторон является прямой уровня.

Таким образом, если некоторая прямая m (рис. 43) перпендикулярна

плоскости a, то она должна быть перпендикулярна двум пересекающимся прямым уровня этой плоскости, одна из которых является горизонталью h, а другая – фронталью f. Эта перпендикулярность прямой двум пересекающимся прямым уровня сохраняется: для горизонтали на горизонтальной плоскости проекций – m ₁ ^ h ₁, а для фронтали f на фронтальной П₂ плоскости проекций – m ₂ ^ f ₂.

Справедливо и обратное положение: если горизонтальная проекция какой-либо прямой перпендикулярна горизонтальной проекции горизонтали данной плоскости, а фронтальная проекция той же прямой перпендикулярна фронтальной проекции фронтальной плоскости, то прямая и плоскость взаимно перпендикулярны.

Рассмотрим пример. Через точку А (рис. 44, а) плоскости, заданной треугольником АВС, требуется провести прямую m, перпендикулярную плоскости.

Вначале (рис. 44, б) в плоскости треугольника строят произвольную горизонталь h плоскости, проходящую, например, через точку А (А₂-I₂,
I₁-A₁), и на горизонтальной плоскости проекций через А₁ проводят прямую m ₁, перпендикулярную h ₁ (A₁-I₁). Затем (рис. 44, в) строят произвольную фронталь f плоскости, также проходящую через точку А (A₁-2₁, 2₂-A₂), и на фронтальной плоскости проекций через А₂ проводят прямую m ₂, перпендикулярную f ₂ (A₂-2₂) – фронтальной проекции фронтали плоскости. Проекции m ₁, m ₂ и являются проекциями искомой прямой m, перпендикулярной плоскости, заданной треугольником АВС.

Если же точка, через которую требуется провести прямую, перпендикулярную заданной плоскости, находится вне ее, то построение проекций этой прямой выполняют согласно условиям: горизонтальная проекция прямой должна располагаться перпендикулярно горизонтальной проекции произвольной горизонтали плоскости, а фронтальная проекция прямой – перпендикулярно фронтальной проекции произвольной фронтали той же плоскости. Для определения положения на чертеже основания перпендикуляра строят проекции точки пресечения его с заданной плоскостью.

Рассмотрим пример решения другой задачи: через точку А (рис. 45, а) требуется провести плоскость, перпендикулярную прямой l общего положения.

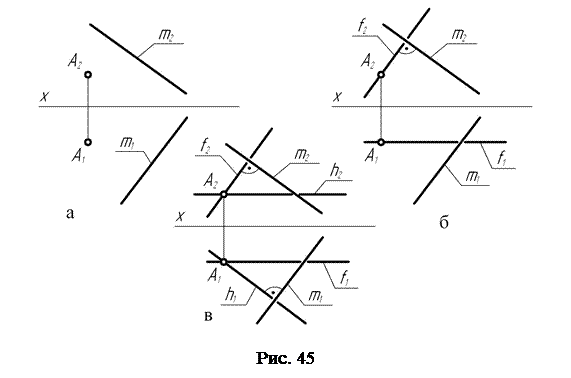В начале (рис. 45, б) на фронтальной плоскости проекций через А₂ проводят фронтальную f ₂ проекцию произвольной фронтали f, перпендикулярно фронтальной l ₂ проекции прямой l. Горизонтальную f ₁ проекцию этой фронтали проводят через А₁ параллельно оси проекций Х.

Затем (рис. 45, в) на горизонтальной плоскости проекций через А₁ проводят горизонтальную h ₁ проекцию произвольной горизонтали h, перпендикулярно горизонтальной l ₁ проекции прямой l. Тогда фронтальную h ₂ проекцию этой горизонтали проводят через А₂ параллельно оси Х.

Пересекающиеся в точке А прямые h и f однозначно определяют положение произвольной плоскости, перпендикулярной заданной прямой l общего положения.

Вопросы для самопроверки

1. В чем состоит условие принадлежности прямой плоскости?

2. В чем состоит условие принадлежности точки плоскости?

3. Какого условия достаточно, чтобы по чертежу можно было бы установить принадлежность точки или прямой проецирующей плоскости?

4. Что такое прямая наибольшего наклона плоскости?

5. Как расположена прямая наибольшего наклона плоскости общего положения к горизонтальной плоскости проекций в пространстве и на чертеже?

6. Как определить на чертеже натуральную величину наибольшего угла наклона плоскости общего положения к горизонтальной плоскости проекций?

7. Как определить на чертеже натуральную величину наибольшего угла наклона плоскости общего положения к фронтальной плоскости проекций?

8. Как построить на чертеже проекции точки пересечения прямой общего положения с проецирующей плоскостью?

9. Как построить на чертеже проекции точки пересечения проецирующей прямой с плоскостью общего положения?

10. Как построить на чертеже проекции линии пересечения проецирующей плоскости с плоскостью общего положения?

11. Изложите последовательность построения на чертеже проекций точки пересечения прямой общего положения с плоскостью общего положения.

12. Как определяется на чертеже видимость проекций прямой и плоскости относительно друг друга?

13. В чем состоит условие перпендикулярности прямой плоскости?

1.4. Последовательность выполнения построений
графического решения задачи 1 [1]

Задача – построить линию пересечения треугольников АВС и ЕДК и показать видимость их в проекциях. Определить натуральную величину треугольника АВС.

Не нашли, что искали? Воспользуйтесь поиском: