Числовая последовательность. Предел числовой последовательности

Определение: Числовой последовательностью будем называть множество чисел: , каждое из которых имеет свой порядковый номер, по которому однозначно определяется по определенному правилу соответствующий элемент последовательности (член последовательности). Если задан 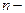ый член последовательности , то по нему можно восстановить и всю последовательность. Например, , тогда имеем числовую последовательность

Если с возрастанием номера члены последовательности приближаются сколь угодно близко к некоторому числу , то это число будем называеть пределом числовой последовательности, при этом числовая последовательность называется сходящейся к числу . Применяются обозначения:

, или .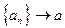

Одно и то же число может быть пределом многих числовых последовательностей. Например,

.

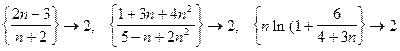Но, если последовательность имеет предел, то этот предел единственен и не зависит от способа его вычисления. Например, вычисляя предел

числовой последовательности с четными , получаем значение предела, равное нулю, с нечетными – значение предела либо +1, либо –1 в зависимости о выбранных значений нечетных чисел. Таким образом предела данной числовой последовательности не существует. Это можно установить, также если восстановить все члены последовательности

.

Видно, что с ростом члены последовательности не приближаются сколь угодно близко ни к какому числу.

Теперь дадим строгое определение предела последовательности:

Определение: Число называется пределом числовой последовательности , если для любого положительного числа найдется такой номер , что при всех члены последовательности удовлетворяют неравенству .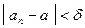

Будем называтьчисловую последовательность бесконечно большой, если с ростом члены последовательности по модулю могут превысить сколь угодно большое положительное число. В этом случае можно записать: 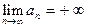( если начиная с некоторого номера все члены последовательности положительны ); или (если начиная с некоторого номера все члены последовательности отрицательны).

Приведем примеры бесконечно больших последовательностей:

,.

Как видим, среди бесконечно больших последовательностей имеются последовательности, имеющие предел, равный бесконечности, предел, равный минус бесконечности. Существуют и последовательности, не имеющие предела (обозначим его отсутствие знаком?).

Действительно, если предел существует, то он – единственен. Если для четных и нечетных знак бесконечности разный, то предел не существует: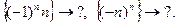

Не нашли, что искали? Воспользуйтесь поиском: