Пример решения задачи 3. Найти производную функции

.

Производная функции равна сумме следующих функций:

;

;

;

.

Здесь кроме правила дифференцирования сложной функции были использованы формулы

.

Задача 4. Найти производную функции

4.1

4.2

4.3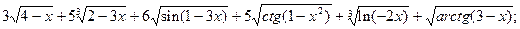

4.4

4.5

4.6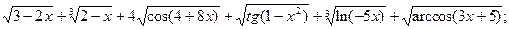

4.7

4.8

4.9

4.10

Пример решения задачи 4 Найти производную функции

.

Решение. Производная функции равна сумме следующих функций:

;

;

Здесь кроме правила дифференцирования сложной функции были использованы формулы:

.

Задача 5. Найти производную функции

5.1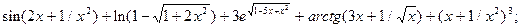

5.2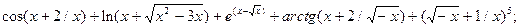

5.3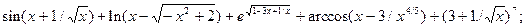

5.4

5.5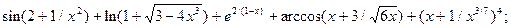

5.6

5.7

5.8

5.9

5.10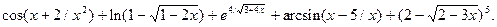

Пример решения задачи 5. Найти производную функции

.

Искомая производная равна сумме следующих функций:

, ,

,

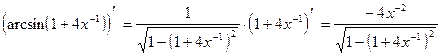Здесь кроме правила дифференцирования сложной функции были использованы формулы:

.

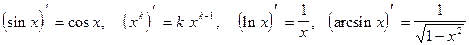Задача 6. Найти производную функции

6.1

6.2

6.3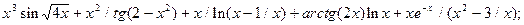

6.4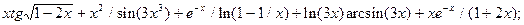

6.5

6.6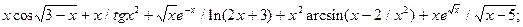

6.7

6.8

6.9

6.10

Пример решения задачи 6. Найти производную функции

.

Искомая производная равна сумме следующих функций:

,

.

Здесь кроме правила дифференцирования сложной функции и свойств производных

были использованы формулы:

Не нашли, что искали? Воспользуйтесь поиском: