
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задача 7. Найти дифференциал функции, используя свойства дифференциала
7.1 
7.2 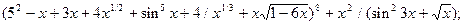
7.3 
7.4 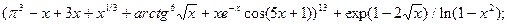
7.5 
7.6 
7.7 
7.8 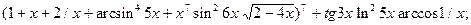
7.9 
7.10 
Пример решения задачи 7. Найти дифференциал функции  , используя свойства дифференциала.
, используя свойства дифференциала.
Решение:

.
В свою очередь,
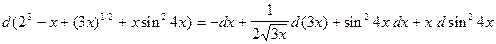 ;
;
 ;
;
 ;
;
 .
.
При решении были использованы свойства дифференциала:
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5. Для сложной функции  имеет место свойство инвариантности дифференциала:
имеет место свойство инвариантности дифференциала:
 ,
,
которое становится очевидным, если учесть правило дифференцирования сложной функции

и определение дифференциала
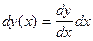 , или
, или  .
.
Задача 8. Найти градиент скалярного поля в точке А(1, 2, 3)
8.1 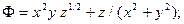 8.6
8.6 
8.2  8.7
8.7 
8.3  8.8
8.8 
8.4  8.9
8.9 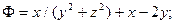
8.5  8.10
8.10 
Пример решения задачи 8. Найти градиент скалярного поля  в точке А(0, 1, 2).
в точке А(0, 1, 2).
Решение: Находим градиент поля в произвольной точке с координатами
 :
:

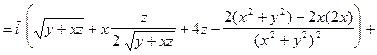
 .
.
Подставляя значения точки А, получаем градиент поля в точке А:
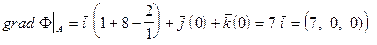 .
.
Задача 9. Найти полный дифференциал функции, используя свойства полного дифференциала. В качестве функции взять скалярное поле Ф Задачи 8.
Пример решения задачи 9. Найти полный дифференциал функции  , используя свойства полного дифференциала.
, используя свойства полного дифференциала.
Решение:

.
В свою очередь:
.
.
 ;
;

 ;
;
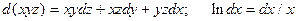 .
.

При решении примера были использованы свойства полного дифференциала:
1.  ;
;
2.  ;
;
3.  ;
; 
4.  ;
;
5. Для сложной функции  имеет место свойство инвариантности полного дифференциала:
имеет место свойство инвариантности полного дифференциала:
 ,
,
очевидность которого, вытекает из правила дифференцирования сложной функции
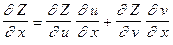 ,
,
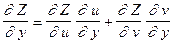 ,
,

и определения полного дифференциала
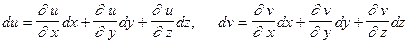 .
.
ГРАФИКИ ФУНКЦИЙ
Не нашли, что искали? Воспользуйтесь поиском: