
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Предел функции в точке. Предел функции на бесконечности
Определение: Число  называется пределом функции
называется пределом функции  в точке
в точке  , если для любой числовой последовательности, сходящейся к числу
, если для любой числовой последовательности, сходящейся к числу  ,
,  , соответствующая числовая последовательность
, соответствующая числовая последовательность 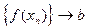 , сходится к числу
, сходится к числу  . Применяемые обозначения:
. Применяемые обозначения:
 или
или  при
при  . Особо подчеркнем здесь выделенное слово «любой», означающее, что значение предела функции, не должно зависеть от вида выбранной последовательности
. Особо подчеркнем здесь выделенное слово «любой», означающее, что значение предела функции, не должно зависеть от вида выбранной последовательности  , и должно оставаться одним и тем же для разных числовых последовательностей
, и должно оставаться одним и тем же для разных числовых последовательностей  .
.
Другими словами, если для разных последовательностей  , соответствующие последовательности
, соответствующие последовательности  стремятся к разным пределам, то предела функции в точке
стремятся к разным пределам, то предела функции в точке  не существует.
не существует.
Определение: Число  называется пределом слева (справа) функции
называется пределом слева (справа) функции  в точке
в точке  , если для любой, сходящейся слева (справа) к числу
, если для любой, сходящейся слева (справа) к числу  числовой последовательности
числовой последовательности 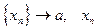 <
<  (
(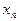 >
>  ) соответствующая числовая последовательность
) соответствующая числовая последовательность 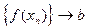 , сходится к числу
, сходится к числу 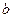 . Для предела функции слева используются обозначения:
. Для предела функции слева используются обозначения:
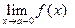 или
или 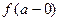 .
.
Аналогично, для предела функции справа:
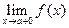 или
или 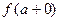 .
.
Теорема: Предел функции в точке существует и равен  тогда и только тогда, когда пределы функции слева и справа в этой точке существуют и оба равны
тогда и только тогда, когда пределы функции слева и справа в этой точке существуют и оба равны  .
.
Продемонстрируем различные ситуации с существованием и не существованием предела функции  , изображенной на Рис.2.
, изображенной на Рис.2.

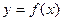















 2
2
 |
 1
1


-5 -4 -3 -2 -1 0 1 2 3 4 5
 -1
-1
 -2
-2
-3
Рис. 2
1)  ;
;
2)  ;
;
3)  ;
;
4) 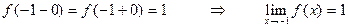 ;
;
5) 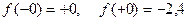 ;
;
6).
Определение: Число  называется пределом функции
называется пределом функции  на
на  (на
(на  ), если для любой бесконечно большой числовой последовательности
), если для любой бесконечно большой числовой последовательности 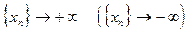 соответствующая последовательность сходится к числу
соответствующая последовательность сходится к числу  , т. е.
, т. е. 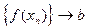 , Применяемые обозначения:
, Применяемые обозначения:

или  .
.
Изобразим на Рис.3 указанные пределы:



 |





 2
2
 |




 |




 -3
-3
Рис. 3
 ,
,
.
Введенные здесь добавки +0 и –0, используемые для уточнения расположения графика функции  относительно ее горизонтальных асимптот
относительно ее горизонтальных асимптот  и
и  , означают, что асимптотическое поведение функции
, означают, что асимптотическое поведение функции 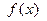 при
при  таково, что функция располагается ниже горизонтальной асимптоты
таково, что функция располагается ниже горизонтальной асимптоты  . А асимптотическое поведение той же функции при
. А асимптотическое поведение той же функции при 
таково, что график функции располагается выше горизонтальной асимптоты  .
.
- Предел функций целочисленного аргумента
Пример 1. Вычислить пределы функций целочисленного аргумента при 
 ;
;  .
.
Решение примера 1
 о
о

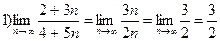 .
.
0
При вычислении предела в числителе и знаменателе пренебрегли постоянными слагаемыми по сравнению с бесконечно большой величиной ~  ;
;
2)  ;
;
Здесь были использованы свойства бесконечности (бесконечно больших величин):
 .
.

 о о
о о
3) 


о о
Здесь сначала пренебрегли постоянными в числителе и знаменателе по сравнению с бесконечно большими слагаемыми. Затем в числителе пренебрегли величиной  по сравнению с бесконечно большой величиной высшего порядка
по сравнению с бесконечно большой величиной высшего порядка  . В знаменателе величина
. В знаменателе величина  , которой пренебрегаем, может рассматриваться как бесконечно малая по сравнению с величиной
, которой пренебрегаем, может рассматриваться как бесконечно малая по сравнению с величиной 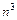 ;
;
 |
 оо
оо
4) 
 .
.
О
Здесь опять постоянной величиной пренебрегали по сравнению с бесконечно большой величиной  , которая сама является бесконечно малой по сравнению с
, которая сама является бесконечно малой по сравнению с  , поскольку для степеней имеет место неравенство
, поскольку для степеней имеет место неравенство 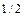 < 2/3.
< 2/3.
В знаменателе по тем же причинам пренебрегли величиной 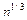 по сравнению с ее квадратом
по сравнению с ее квадратом  . Последняя является бескончно большой величиной высшего порядка по сравнению с величиной
. Последняя является бескончно большой величиной высшего порядка по сравнению с величиной 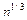 .
.
Замечание: При сравнении порядков бесконечно больших степенных функций можно пользоваться шкалой бесконечно больших функций);
5) 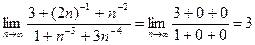 .
.
6)
Здесь учтено, что бесконечно большие величины в отрицательной степени становятся бесконечно малыми. Действительно, например:
 ;
;
 о
о
7) 
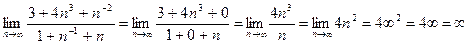
0
Здесь пренебрегли постоянными величинами по сравнению с бесконечно большими, а также учтено, что бесконечно большая величина в отрицательной степени является бесконечно малой величиной.
Не нашли, что искали? Воспользуйтесь поиском: