Задача 2 . Вычислить пределы функций, если они существуют, при и при и изобразить их графически

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

ДИФФЕРЕНЦИРОВАНИЕ

· Производные.

· Дифференциалы.

· Частные производные.

· Полный дифференциал.

· Градиент скалярного поля.

Задача 1. Найти производную функции

1.1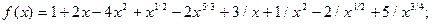

1.2

1.3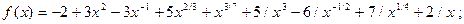

1.4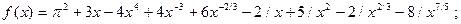

1.5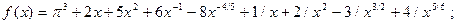

1.6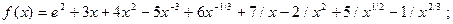

1.7

1.8

1.9

1.10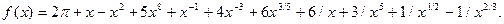

Пример решения задачи 1. Найти производную функции

.

Поскольку производная суммы функций равна сумме производных, имеем:

.

Первые три слагаемые обращаются в ноль ввиду того, что производная константы равна нулю. Оставшиеся производные выпишем отдельно, вычисляя производные по формуле .

.

Задача 2. Найти производную функции

2.1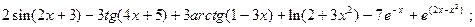

2.2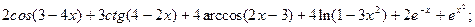

2.3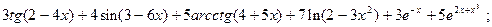

2.4

2.5

2.6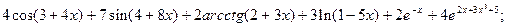

2.7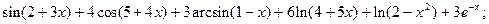

2.8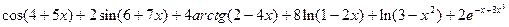

2.9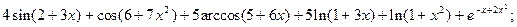

2.10 ;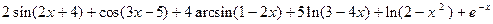

Пример решения задачи 2. Вычислить производную функции

.

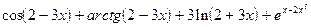Производная функции, как и в первом примере, равна сумме следующих функций:

;

;

;

.

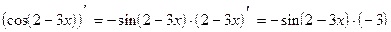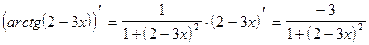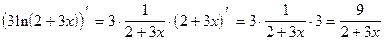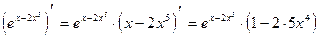Здесь было использовано правило дифференцирования сложной функции, а также формулы дифференцирования:

.

Задача 3. Найти производную функции

3.1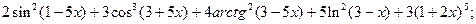

3.2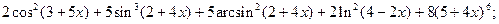

3.3

3.4

3.5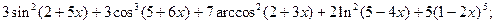

3.6 ;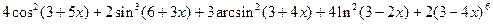

3.7

3.8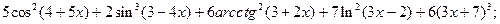

3.9

3.10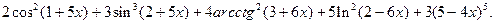

Не нашли, что искали? Воспользуйтесь поиском: