Пр.1 Построим график функции .

ОДЗ: .

С учетом нечетности функции 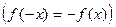произведем сужение области определения, отбрасывая из рассмотрения область отрицательных значений аргумента: ОДЗ: .

Выясним поведение функции на границах ОДЗ:

;

.

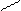
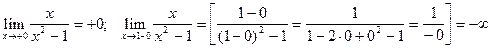Нанесем на координатную плоскость результаты вычисления пределов (Рис. 1):

y y

Рис.1 Рис. 2

0 1 x 0 1 x

Теперь можно нарисовать предположительный вид графика функции (Рис. 2).

Убедимся, в справедливости нашего предположения. Проверим, что на графике отсутствуют локальные экстремумы.

Найдем первую производную функции, попытаемся приравнять ее нулю:

.

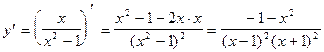Поскольку в числителе имеем отрицательное число, производная в нуль не обращается. Следовательно, критических точек на графике функции нет, как нет и дифференцируемых экстремумом.

Найдем, в каких точках производная не существует или обращается в бесконечность. Приравнивая знаменатель производной нулю, получаем значение такой точки: . Однако из Рис. 2 мы уже знали, что при производная обращается в бесконечность (слева от это , справа ). Таким образом, на Рис. 2 график изображен правильно.

Сделаем одно уточнение. Найдем под каким углом пересекает начало координат график функции. Для этого подставим абсциссу начала координат в найденную производную:

.

Таким образом пересечение графика функции начала координат осуществляется под углом 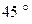, примерно так, как мы и нарисовали.

С учетом нечетности функции, продолжим график функции на всю числовую ось, и окончательно получим искомый график (Рис. 3).

y Рис. 4

-1 0 1 x

Не нашли, что искали? Воспользуйтесь поиском: