Сферические координаты положения главной оси гироскопа

При рассмотрении теории навигационных гироскопических устройств пользуются двумя системами координат: горизонтной и инерциальной.

Система координат, связанная неподвижно с земными плоскостями называется горизонтной.

Гироскопические приборы и системы, используемые в судовождении, имеют целью стабилизировать различные направления (меридиана, отвесной линии и другие) относительно земных плоскостей, поэтому рассмотрим вначале, как определяется положение главной оси гироскопа относительно горизонтной системы -координат (ГСК).

ГСК образуется пересечением трех основных земных плоскостей: плоскости меридиана, плоскости горизонта и плоскости первого вертикала. Оси ГСК называются: полуденной линией (NS) и обозначается N; отвесной линией (z_n n) и обозначается η. и линией EW, которая обозначает Е. Начало ГСК принимается в точке подвеса гироскопа (0).

Надгоризонтная часть ГСК изображена на рис. 3.

Пусть положительный конец оси X гироскопа отклонена от N в плоскости горизонта к востоку (Е) на угол α и приподнят над плоскостью горизонта на угол β (Положительным концом оси Х называется тот, откуда вращение ротора гироскопа видно против движения часовой стрелки).

Спроектируем ось Х гироскопа на плоскость горизонта. Получим проекцию х.'

Положение главной оси гироско-па относительно земных плоскостей (ГСК) определится углами α и β Угол α, заключенный между полуденной линией NS и проекцией оси Х гироскопа на плоскость горизонта (х^’), называется азимутом. Азимут отсчитывается от точки N.

Рис.3 Угол β, заключенный между осью Х гироскопа и её проекцией х' на плоскость горизонта называется высотой. Высота отсчитывается от плоскости горизонта. Азимут и высота является сферическими координатами главной оси гироскопа в горизонтной системе координат и определяют её положение относительно земных плоскостей.

Азимут и высота имеют положительные значения при отклонении положительного конца оси х гироскопа к востоку и вверх. На рис.3 углы α и β положительны.

Для определения положительных направлений осей ГСК в теории гироскопа принимают правую систему координат, при которой увеличение положительных углов усматривается с положительного направления осей, как движение против часовой стрелки.

Увеличение угла β против движения часовой стрелки видно с востока (Е), а угла α снизу. Следовательно, при заданном направлении оси Х гироскопа, положительное направление оси У к Е, оси Z- вниз, как показано на рис.3.

При рассмотрении свойств гироскопа вместо ГСК за условно неподвижную систему необходимо принимать систему координат, связанную с инерциальным пространством. Обычно инерциальное пространство ограничивается солнечной системой. Оси 0 ξ*,η*, У * инерциальной системы координат (ИСК) произвольно ориентированы в пространстве. Положение главной оси гироскопа в ИСК определяется сферическими координатами γ (гамма) и ψ (пси). Начало ИСК, как и ГСК, расположено в точке подвеса гироскопа.

Если оси ИСК и ГСК совпадают, то углы, определяющие положение оси Х гироскопа, попарно равны, т.е. α = γ, a β = ψ. Если указанные системы координат не совпадают, то. α ≠ γ, a β ≠ ψ.

ЛЕКЦИЯ №2

ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ГИРОСКОПА

К динамическим характеристикам (параметрам) гироскопа относятся:

1. Угловая скорость вращения ротора.

2. Момент инерции ротора.

3. Кинетический момент.

Рассмотрим последовательно каждую из перечисленных динамических характеристик гироскопа.

1. Угловая скорость вращения ротора.

Вращение любого твердого тела характеризуется тремя элементами:

- положением оси, вокруг которой происходит вращение;

- направлением самого вращения;

- величиной угловой скорости вращения.

Этими же элементами характеризуется и вращение гироскопа.

Собственное вращение ротора происходит вокруг его оси симметрии - главной оси гироскопа с определенной угловой скоростью. Угловой скоростью вращающегося ротора (Ω)называется величина, учитывающая скорость изменения угла поворота ротора (У). Аналитическая запись этого определения имеет вид:

Ω =dy/dt (1)

Условно все элементы собственного вращения ротора гироскопа изображаются вектором угловой скорости Ω,. Вектор Ω. направлен по оси, вокруг которой происходит вращение и в ту сторону, откуда вращение наблюдается против движения часовой стрелки (рис.4). Величина вектора изображает в определенном масштабе величину угловой скорости вращения.

Угловая скорость вращения определяется числом радиан в секунду или в технике числом оборотов в минуту.

Соотношение числа оборотов в минуту и числа радиан в секунду определяется выражением:

Ω =π·n/30 (рад/сек) (2)

n = 30·Ω/π (об/мин) (3)

где n - число оборотов в минуту.

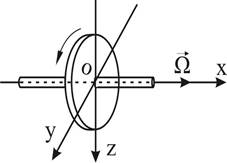Ротор гироскопа с тремя степенями свободы имеет возможность вращаться не только вокруг главной оси Х, но и вместе с ней вокруг оси У или Z. Если вращающийся гироскоп поворачивается вокруг оси У или Z, то вектор результирующей угловой скорости можно представить в виде двух составляющих: вектора угловой скорости вращения главной оси гироскопа вокруг оси У или Z и вектора угловой скорости собственного вращения ротора Ω. Угловая скорость вращения ротора

Рис.4 может достигать 10000 - 30000 об/мин, и во много раз больше скорости вращения гироскопа вокруг оси У или Z. Пренебрегая по малости угловой скоростью вращения гироскопа вокруг осей У и Z, результирующую угловую скорость вращения можно считать равной Ω и направленной по главной оси Х гироскопа.

Не нашли, что искали? Воспользуйтесь поиском: