Теорема об изменении кинетического момента

Эта теорема определяет закон изменения вектора кинетического момента Н при действии на вращающееся тело моментов внешних сил. Этот закон имеет несколько формулировок, одна из которых относится к изменению кинетического момента системы относительно точки, которая и будет нас интересовать, т.к. главная ось гироскопа совершает движение относительно неподвижной точки -точки подвеса гироскопа.

Теорема об изменении вектора кинетического момента, или закон моментов, применительно к гироскопу формулируется следующим образом.

Производная по времени от вектора кинетического момента вращающегося гироскопа относительно точки равна вектору главного момента всех внешних сил (L), действующих на гироскоп, относительно той же точки

L =dH/dt (8)

Анализ формулы (8) показывает, что кинетический момент величина переменная и является функцией времени. Во всех случаях изменение вектора Н во времени определяется вектором главного момента внешних сил (L), приложенных к гироскопу. Если векторы Н и L совпадают или диаметрально противоположны, то L характеризует изменение модуля Н. Если Н и L взаимно перпендикулярны, то L характеризует изменение только направления вектора Н. Если Н и L составляют угол, отличный от О⁰, 90°, 180°и 270° то L характеризует и изменение модуля вектора Н, и изменение его направления.

Известно, что производная по времени от вектора равна линейной скорости движения конца этого вектора, т.е.

dH/dt = V (9)

где: V - вектор линейной скорости конца вектора Н. Сравнивая формулы 8 и 9, можно написать

V=L (10)

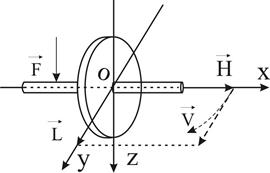Равенство (10) дает геометрическое толкование теоремы об изменении кинетического момента, известное под названием теоремы Резаля.

Теорему Резаля применительно к вращающемуся гироскопу можно сформулировать так: вектор линейной скорости V конца вектора кинетического момента Н гироскопа относительно точки подвеса 0, равен вектору главного момента L всех внешних сил, действующих на гиро-

Рис. 6 скоп, относительно той же точки.

Анализ закона моментов показывает, что под действием момента L внешней силы F вектор Н (главная ось X гироскопа) будет перемещаться в инерциальном пространстве не в направлении действия внешней силы, а в направлении действия момента этой силы, (рис.6).

Этот закон имеет значение для понимания физической сущности свойств гироскопа.

ЛЕКЦИЯ 3

ТЕМА: СВОЙСТВА ГИРОСКОПА

I. Технические уравнения движения гироскопа

Ранее было показано, что в результате действия момента внешней силы главная ось гироскопа перемещается относительно первоначального положения.

Следовательно, можно сказать, что в общем случае гироскоп изменяет свое положение относительно инерциального пространства и земных плоскостей, т.е. сферические координаты осей гироскопа непрерывно изменяется, для определения положения гироскопа достаточно знать положение его главной оси Х. Возьмем ИСК и мгновенное положение главной оси Х гироскопа в этой системе координат. Тем самым будет определено положение осей Y и Z гироскопа (рис.7). На рис.7 показано положение главной оси X

Рис.7 гироскопа, отклоненной на углы γ и ψ

Из рис. 7 видно, что угловая скорость вращения гироскопа вокруг оси I_* ИСК определится вектором , а вокруг оси Y гироскопа - вектором .Тогда угловая скорость вращения гироскопа вокруг оси Z гироскопа определится вектором r = γ·cosψ.

Для определения сферических координат положения гироскопа в инерциальном пространстве γ и ψ необходимо знать законы движения главной оси X гироскопа вокруг осей X Y и Z. Эти законы могут быть найдены из технических уравнений движения гироскопа. Технические уравнения, или усеченные уравнения Эйлера, имеют вид:

(11)

где: I и А – полярный и экваториальный моменты инерции соответственно; и – абсолютные (относительно ИСК) угловые скорости движения главной оси гироскопа вокруг осей У и Z; L_y и L_z – моменты внешних сил, действующих вокруг осей У и Z соответственно.

Уравнение 1 – системы определяет постоянную угловую скорость собственного вращения гироскопа, поэтому в дальнейшем оно рассматриваться не будет.

Уравнения 2 и 3 системы характеризуют величины моментов внешних сия, действующих по осям У и Z гироскопа соответственно, или проекции моментов на указанные оси. Первые слагаемые левых частей уравнений (11) называются инерциальными членами, вторые слагаемые – гироскопическими членами технических уравнений движения гироскопа.

Анализ уравнений (11) показывает, что угловые скорости абсолютного движения q и r гироскопа можно определить по значениям моментов внешних сил L_y и L_z. Рассчитав значения q и r, можно определить сферические координаты положения главной оси Х гироскопа в ИСК, т.е. углы γ и ψ. Чтобы найти углы γ и ψ, необходимо знать угловые скорости и . Из рис.7 видно, что указанные скорости связаны следующими соотношениями:

; (12)

(13)

Не нашли, что искали? Воспользуйтесь поиском: