
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Свойства гироскопа с тремя степенями свободы
Принцип действия современных навигационных гироскопических приборов и систем основан на использовании свойств гироскопа, к которым относятся:
A. Устойчивость положения главной оси гироскопа.
Б. Прецессионное движение гироскопа (прецессия),
B. Нутационное движение гироскопа (нутация).
А Устойчивость положения главной оси гироскопа Устойчивость положения главной оси гироскопа является основным свойством гироскопа и характеризуется:
• неизменностью положения оси X свободного гироскопа относительно инерциального пространства;
• нечувствительностью гироскопа к ударам.
Для доказательства основного свойства гироскопа используют технические уравнения. Задача сводится к определению, углов γ и ψ – сферических координат положения главной оси гироскопа относительно ИСК. Для отыскания значений этих углов воспользуемся ранее выведенными формулами:  и
и  откуда
откуда
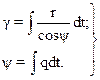 (14)
(14)
Для решения системы уравнений (14) предварительно необходимо определить законы изменения угловых скоростей q и r, для чего воспользуемся техническими уравнениями 2 и 3 системы (11). Для свободного гироскопа Ly= Lz = 0. Тогда уравнения 2 и 3 (11) после несложных преобразований примут вид:
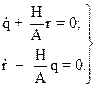 (15)
(15)
 Обозначив k=Н/А, и решив полученные дифференциальные уравнения (15) получим законы изменения углов γ и ψ во времени:
Обозначив k=Н/А, и решив полученные дифференциальные уравнения (15) получим законы изменения углов γ и ψ во времени:
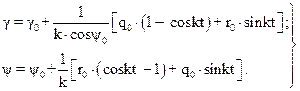 (16)
(16)
где: γ0 и ψ0 – начальные значения координат;
γ и ψ – текущие значения координат;
k – круговая частота;
kt – фаза колебаний;
q0 и r0 – угловые скорости движения гироскопа по углам γ0 и ψ0 соответственно.
Анализ системы уравнений показывает, что первое уравнение – есть закон изменения угла γ, который показывает, что при большой скорости собственного вращения гироскопа угол γ, благодаря малости второго слагаемого, остается близким к начальному значению γ0, поэтому можно принять
γ0 = γср=const (17)
Второе уравнение системы (16) – есть закон изменения угла ψ в котором ψ0 =const и не зависит от времени. Второе слагаемое – периодическая функция от времени, характеризующая колебательный процесс и позволяющая определить величину угла отклонения оси X от её начального положения. Амплитудное значение угла очень мало, т. к. круговая частота очень велика, т.е.Н»А. На основании изложенного можно сделать вывод, что периодическая функция (второе слагаемое выражения) – есть функция времени, которая изменяет начальный угол ψ0, незначительно и создает вокруг него колебания с большой частотой и малой амплитудой. Эта амплитуда колебаний уменьшается с увеличением Н. Пренебрегая по малости вторым слагаемым, получим
ψ0 = ψср=const (18)
Таким образом, проанализировав законы изменения углов γ и ψ, видно, что при большой угловой скорости собственного вращения гироскопа углы γ и ψ остаются близкими к их начальным значениям γ0 и ψ0, т.е. главная ось X свободного гироскопа сохраняет свое положение относительно инерциального пространства неизменным с точностью до величины периодического члена.
Для доказательства основного свойства гироскопа можно воспользоваться теоремой Резаля. Это доказательство проще, но не строго объясняет основное свойство.
Для свободного гироскопа, как это следует из определения, L=0, и теорему Резаля. можно записать в следующем виде:  .
.
Это означает, что 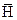 =const, т.е. вектор кинетического момента свободного гироскопа остается постоянным по величине и направлению в инерциальном пространстве, а т.к. его направление всегда совпадает с главной осью X гироскопа, то можно считать, что главная ось свободного гироскопа сохраняет неизменным первоначально заданное направление в инерциальном пространстве. Следовательно, если глазная ось X свободного гироскопа направлена на Солнце или звезду в начальные момент времени, то в дальнейшем она все время будет указывать это направление.
=const, т.е. вектор кинетического момента свободного гироскопа остается постоянным по величине и направлению в инерциальном пространстве, а т.к. его направление всегда совпадает с главной осью X гироскопа, то можно считать, что главная ось свободного гироскопа сохраняет неизменным первоначально заданное направление в инерциальном пространстве. Следовательно, если глазная ось X свободного гироскопа направлена на Солнце или звезду в начальные момент времени, то в дальнейшем она все время будет указывать это направление.
Пользуясь свободным гироскопом, можно проследить суточное вращение Земли. Действительно, если главная ось свободного гироскопа сохраняет неизменным свое первоначальное направление в инерциальном пространстве, а сама Земля вращается, то наблюдатель должен увидеть, что ось X свободного гироскопа поворачивается относительно Земли. Если направить главную ось X свободного гироскопа на Солнце, то она, сохраняя направление неизменным, будет вместе с Солнцем изменять свой азимут и высоту, т.к. плоскости меридиана и горизонта вращаются в инерциальном пространстве вместе с Землей. Такое изменение положения главной оси гироскопа относительно земных плоскостей1 называется видимым движением.
С точки зрения физики основное свойство гироскопа объясняется инерцией. Все точки вращающегося ротора имеют скорости, направленные в плоскости вращения, и по закону инерции каждая точка стремится сохранить неизменной в пространстве плоскость своего вращения. На этом основании плоскость вращения всего ротора, а следовательно, и его главная ось также сохраняют неизменными в пространстве первоначальные направления.
Вполне очевидно, что чем больше угловая скорость вращения ротора, тем большим кинетическим моментом обладает гироскоп и тем сильнее выражено его основное свойство.
Нечувствительность гироскопа к удару является положительным качеством гироскопа. Удар – это кратковременное (мгновенное) действие момента внешней силы. Доказательство этого качества гироскопа производится решением технических уравнений. Не приводя решений уравнений, напишем законы изменения углов γ и ψ гироскопа после удара:
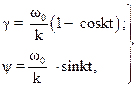 (19)
(19)
где ω0 – начальная угловая скорость оси X гироскопа.
Выражения (19) есть законы изменения углов γ и ψ после удара. Анализ системы уравнений показывает, что главная ось X гироскопа совершает гармонические колебания в плоскости углов γ и ψ около положения равновесия, определяемого углами:
ψр = 0; γр = ω0/k. (20)
Эти колебания имеют очень малую амплитуду и большую частоту. Практически при очень большой скорости вращения ротора гироскопа эти колебания неощутимы.
Отклонение оси X гироскопа от первоначального положения при ударе происходит только непосредственно в момент удара, и оно столь мало, что им можно пренебречь и считать;– удар практически не изменяет положения оси гироскопа в пространстве.
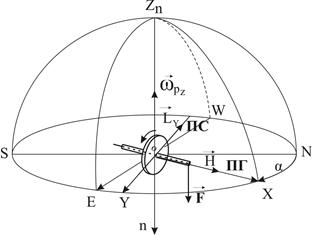
Б. Прецессионное движение гироскопа. Пусть на гироскоп действует внешняя сила F, как показано на рис. 7. Эта сила стремится повернуть гироскоп вокруг оси Y. Следовательно, момент внешней силы (LY) будет действовать вокруг оси Y. Рассмотрим поведение гироскопа в этом случае. Под влиянием момента внешней силы LY движение гироскопа определяется выражениями (12) и (13), значения q и r определяются из технических уравнений:
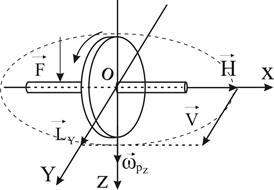
 (21)
(21)
В нашем случае LZ = 0, и k=Н/А, отсюда уравнения (21) после несложных преобразований примут вид:
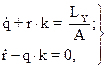 (22)
(22)
Решение дифференциальных уравнений (22)
рис.7 приводит к выражениям вида:
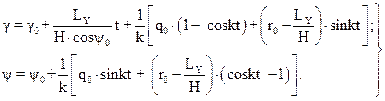 (23)
(23)
Система уравнений (23) характеризует законы изменения углов γ и ψ при действии на гироскоп момента внешней силы LY
Второе уравнение системы характеризует закон изменения угла ψ и позволяет определить текущее значение этого угла на любой момент времени. Второе слагаемое характеризует изменение утла ψ и представляет собой периодическую функцию. При большой скорости вращения ротора гироскопа частота колебаний главной оси X велика, а второе слагаемое в целом мало. Это означает, что угол ψ остается практически равным ψ0 т.е. не изменяется ψ0 = const.
Первое уравнение показывает, что угол γ с течением времени изменяется. Второе слагаемое 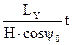 , есть произведение угловой скорости на время. Оно показывает изменение величины угла γ под действием момента внешней силы Ly; главная ось X гироскопа движется не в направлении действия силы F, а в плоскости, перпендикулярной этому направлении. Такое движение гироскопа называется прецессионным (рис.7). Третье слагаемое характеризует колебательное движение оси Z гироскопа, которое называется нутацией. При большой скорости собственного вращения гироскопа амплитуда этих колебаний, как и в законе для угла ψ, столь мала, а частота настолько велика, что колебания практически неощутимы. Фактическое движение гироскопа, оцениваемое системой уравнений (23), называется псевдорегулярной прецессией
, есть произведение угловой скорости на время. Оно показывает изменение величины угла γ под действием момента внешней силы Ly; главная ось X гироскопа движется не в направлении действия силы F, а в плоскости, перпендикулярной этому направлении. Такое движение гироскопа называется прецессионным (рис.7). Третье слагаемое характеризует колебательное движение оси Z гироскопа, которое называется нутацией. При большой скорости собственного вращения гироскопа амплитуда этих колебаний, как и в законе для угла ψ, столь мала, а частота настолько велика, что колебания практически неощутимы. Фактическое движение гироскопа, оцениваемое системой уравнений (23), называется псевдорегулярной прецессией
Прецессионное и нутационное движения совершается одновременно. Главная ось гироскопа поворачивается вокруг точки подвеса 0 с угловой скоростью, равной угловой скорости прецессии 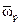 и одновременно совершает нутационные колебания с большой частотой и малой амплитудой.
и одновременно совершает нутационные колебания с большой частотой и малой амплитудой.
Угловая скорость прецессии гироскопа определяется равенством: 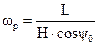 , при ψ0 = 0
, при ψ0 = 0
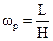 . (24)
. (24)
Формула (24) выражает основной закон прецессии: угловая скорость прецессионного движения гироскопа прямо пропорциональна моменту внешних сил (L) и обратно пропорциональна кинетическому моменту Н
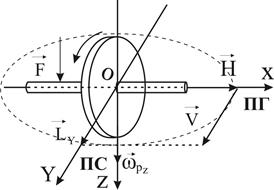 Прецессионное движение гироскопа объясняется и теоремой Резаля. Согласно этой теореме, линейная скорость движения конца вектора кинетического момента вращающегося гироскопа равна по величине и направлению главному моменту всех внешних сил, приложенных к гироскопу.
Прецессионное движение гироскопа объясняется и теоремой Резаля. Согласно этой теореме, линейная скорость движения конца вектора кинетического момента вращающегося гироскопа равна по величине и направлению главному моменту всех внешних сил, приложенных к гироскопу.
На рис.7 и 8 показан гироскоп, к которому приложена сила F, стремящаяся повернуть его
Рис.8 вокруг оси У. Построим вектор момента этой внешней силы Ly. Согласно принятому в механике правилу, вектор Ly должен лежать на оси, вокруг которой действует сила, и из его конца действие силы должно усматриваться против движения часовой, стрелки.
Согласно формуле (10) V = L, где V - вектор линейной скорости движения конца вектора Н. Построим у конца вектора Н вектор V так, чтобы он по величине и направлению был равен вектору Ly. Вектор V покажет нам направление и скорость движения конца вектора Н. Из рисунка видно, что конец вектора Н вместе с главной осью X гироскопа начнет совершать движение вокруг оси Z гироскопа, т.е. в плоскости, перпендикулярной направлении действия силы F. Ось, вокруг которой совершается прецессионное движение гироскопа, называется осью прецессии.
Определим угловую скорость прецессии гироскопа 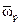 . Для этого достаточно определить угловую скорость одной точки гироскопа, например точки, определяющей конец вектора Н. Так как при вращательном движении точки угловая скорость её равна линейной, деленной на радиус вращения, то, как следует из рис. 8,
. Для этого достаточно определить угловую скорость одной точки гироскопа, например точки, определяющей конец вектора Н. Так как при вращательном движении точки угловая скорость её равна линейной, деленной на радиус вращения, то, как следует из рис. 8, 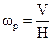 , но V = L следовательно.
, но V = L следовательно. 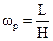
Направление вектора угловой скорости прецессии 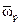 определится по известному нам правилу: из конца этого вектора прецессионное движение должно усматриваться против движения часовой стрелки.
определится по известному нам правилу: из конца этого вектора прецессионное движение должно усматриваться против движения часовой стрелки.
Рассматривая рис.7 и 8, видим, что в прецессионном движении конец вектора Н стремится к концу вектора L. Конец вектора Н назовем полюсом гироскопа (ПГ), а конец вектора L – полюсом внешней силы (ПС). Для определения направления прецессии пользуются следующим правилом; в прецессионном движении полюс гироскопа стремится к полюсу силы по кратчайшему пути. Это правило называется правилом полюсов.
Правив полюсов позволяет решать следующие задачи, связанные с практикой использования навигационных гироскопических приборов и систем.
Задача 1. Зная направление вращения ротора гироскопа (направление вектора Н) и направление действия силы F, действующей на гироскоп, можно определить направление прецессии, т.е. направление вектора 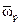 .
.
Эта задача уже была решена при рассмотрении рис. 7, рис. 8.
 Задача 2. Зная направление вращения ротора гироскопа, т.е.Н, и направление вектора угловой скорости прецессии
Задача 2. Зная направление вращения ротора гироскопа, т.е.Н, и направление вектора угловой скорости прецессии 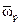 , можно определить направление действия силы F и момента этой силы L. Такая задача, например, решается на практике при ускоренном приведении ГК в меридиан. На рис. 9 показано положение главной оси гироскопа относительно меридиана. Требуется приложить к гироскопу такой, момент силы, чтобы его главная ось X в результате прецессии пришла в меридиан. Для определения направления вектора Ly рассуждаем так: по правилу полюсов ПГ стремится к ПС кратчайшим путем. По условию задачи гирокомпас должен прецессировать к меридиану, т.е. вектор
, можно определить направление действия силы F и момента этой силы L. Такая задача, например, решается на практике при ускоренном приведении ГК в меридиан. На рис. 9 показано положение главной оси гироскопа относительно меридиана. Требуется приложить к гироскопу такой, момент силы, чтобы его главная ось X в результате прецессии пришла в меридиан. Для определения направления вектора Ly рассуждаем так: по правилу полюсов ПГ стремится к ПС кратчайшим путем. По условию задачи гирокомпас должен прецессировать к меридиану, т.е. вектор 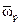 должен быть направлен по оси прецессии Z
должен быть направлен по оси прецессии Z
рис.9 вверх. Следовательно, ПС должен лежать на
оси У к западу. Положение же ПС определяет направление вектора Ly Зная Ly, легко определить направление F
Задача 3. Зная направление действия силы F, а значит вектора L, а также направление прецессии гироскопа (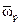 )можно определить направление вращения ротора, т.е. направления вектора Н.
)можно определить направление вращения ротора, т.е. направления вектора Н.
Такая задача может решаться при определении направления вращения ротора гироскопа гироазимута. Для этого достаточно определить положение ПГ. Чтобы определить положение ПГ, надо приложить к гироскопу произвольную силу и проследить, какой конец главной оси гироскопа прецессирует к ПС. Такая задача может быть определена при рассмотрении рис.9.
В заключение отметим, что прецессия гироскопа прекращается сразу же после прекращения действия момента внешней силе. В силу этого свойства всякие толчки и удары, которые передаются от корпуса судна на гирокомпас или гироазимут, вызывают прецессию гироскопа только в течении.своего действия, а т.к. оно кратковременно, то главная ось гироскопа практически не изменяет первоначального направления.
В Нутационное движение гироскопа Из технических уравнений для свободного гироскопа имеем:
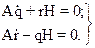 (25)
(25)
следует, что 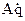 и
и 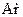 являются инерционными членами. Допустим, что они равны нулю, т.е.
являются инерционными членами. Допустим, что они равны нулю, т.е.  , тогда
, тогда
 (26)
(26)
Так как Н#0, то r = q = 0, следовательно, нутационное движение гироскопа совершается под действием инерционных сил. Нутация гироскопа носит колебательный характер. Колебания главной оси гироскопа совершаются с большой частотой и малой амплитудой.
Чем больше кинетический момент гироскопа, - тем меньше амплитуда нутационных колебаний и больше частота.
Лекцая 4
Тема: МОМЕНТ ГИРОСКОПИЧЕСКОЙ РЕАКЦИЙ
При рассмотрении вопроса о прецессии гироскопа мы видели, что под действием приложенной внешней силы главная ось гироскопа движется не по направлению силы, а перпендикулярно ей и оказывает этой силе сопротивление.
 Если, например, пальцем нажать на опоры главной оси гироскопа с некоторой силой F (рис.10), то со стороны опор этой оси к пальцу прикладывается противодействующая сила реакции R, уравновешивающая нажим, т.е. силу F Рис.10. Сила R реакции опор гироскопа называется гироскопической реакцией, а момент этой силы - моментом гироскопическое реакции, или гироскопическим моментом LR. Силы F и R равны по величине, но противоположны по направлению. Поэтому момент гироскопической реакции равен по величине, но противоположен по направлению моменту L приложенной силы:
Если, например, пальцем нажать на опоры главной оси гироскопа с некоторой силой F (рис.10), то со стороны опор этой оси к пальцу прикладывается противодействующая сила реакции R, уравновешивающая нажим, т.е. силу F Рис.10. Сила R реакции опор гироскопа называется гироскопической реакцией, а момент этой силы - моментом гироскопическое реакции, или гироскопическим моментом LR. Силы F и R равны по величине, но противоположны по направлению. Поэтому момент гироскопической реакции равен по величине, но противоположен по направлению моменту L приложенной силы:
LR= - L (27)
Рис.10
Угловая скорость прецессии определяется по формуле ωР =L/H отсюда:
L = ωР·H. (28)
Следовательно
LR=- ωР H. (29)
Таким образом, момент гироскопической реакции равен произведению кинетического момента на угловую скорость прецессии и направлен в сторону, противоположную моменту внешней силы, вызвавшей прецессию гироскопа,
Для определения направления вектора гироскопического момента пользуются правилом, которое вытекает непосредственно из (рис. 10): направление вектора LR таково, что он как бы стремится совместить по кратчайшему пути вектор кинетического момента Н гироскопа с вектором угловой скорости прецессии ωР.
Гироскопический момент препятствует главной оси гироскопа повороту в направлении действия силы.
Из формулы (29) следует, что появление гироскопического момента всегда обусловливается наличием двух вращений: прецессии гироскопа, которая, в свой очередь, возникает из действия на гироскоп момента внешней силы и вращения ротора.
Момент гироскопической реакции возникает при всяком вынужденном повороте гироскопа вокруг оси, не совпадающей с осью вращения. Чтобы убедиться в этом, достаточно попробовать повернуть руками главную ось гироскопа.
Тогда мы почувствуем, что эта ось сопротивляется повороту, стремятся вырваться из рук и оказывает на наши руки давление. По ощущению в руках мы убедимся, что при повороте в горизонтальной плоскости ось гироскопа давит на руки вертикальной парой сил, и наоборот.
Чтобы продемонстрировать появление гироскопического момента при вынужденном повороте, лишим гироскоп, показанный на рис.11, возможности поворачиваться вокруг оси У. Такой гироскоп будет иметь две степени свободы: вокруг оси X и вокруг оси Z. Возьмем прибор в руки и будем поворачивать его вместе с подставкой, вокруг оси У с некоторой угловой скоростью ωву. Такой поворот гироскопа называется вынужденным поворотом, или вынужденной прецессией.
Мы увидим, что гироскоп, совершая вынужденную прецессию вокруг оси У, начнет одновременно поворачиваться вокруг оси Z. так, чтобы вектор Н кратчайшим путем совместился с вектором ωву (сверху этот поворот будет виден против движения часовой стрелки).
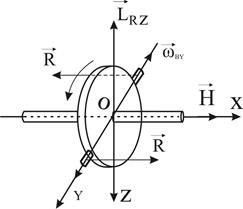 Таким образом, на гироскоп передается пара сил R, устанавливающая его ось определенным образом. Момент этой пары является гироскопический моментом Lrz, возникающим вследствие вынужденной прецессии. В этом можно убедиться, определив направление вектора Lrz, в данном примере по правилу, которое приводилось выше.
Таким образом, на гироскоп передается пара сил R, устанавливающая его ось определенным образом. Момент этой пары является гироскопический моментом Lrz, возникающим вследствие вынужденной прецессии. В этом можно убедиться, определив направление вектора Lrz, в данном примере по правилу, которое приводилось выше.
Величина гироскопического момента при вынужденном повороте (вынужденной прецессии) гироскопа определится из формулы:
Рис.11 LRZ = - ωву. (30)
Не вникая в физическую природу гироскопического момента, отметим, что он является следствием так называемых кориолисовых сил инерции, которые возникают при повороте вращающегося тела вокруг оси, не совпадающей с осью собственного вращения. В наших примерах гироскопический момент возникал при одновременных поворотах гироскопа: собственного вращения ротора вокруг оси X и прецессии (вынужденной прецессии) главной оси вокруг оси У или Z.
ЛЕКЦИЯ 5
Тема: УРАВНЕНИЯ ДВИЖЕНИЯ ГИРОСКОПА
Не нашли, что искали? Воспользуйтесь поиском: