Процедуры сглаживания

Процедуры сглаживания строят таким образом, чтобы они обеспечивали минимизацию случайных отклонений уровней временного ряда от некоторой гладкой кривой предполагаемого тренда (закономерности) изучаемого процесса. Наиболее простой и довольно распространенный прием заключается в расчете осреднении текущего уровня временного ряда по некоторой совокупности окружающих его точек. Причем, эта операция перемещается вдоль временного ряда, в связи с чем, ее обычно называют процедурой скользящей средней. В самом простом варианте эту процедуру осуществляют с помощью линейной функции, а сглаживающая группа состоит из предыдущей, текущей и последующей точек. В более сложных ситуациях сглаживание проводят с помощью нелинейной функции и используют сглаживающую группу произвольного числа точек.

Рассмотрим простейший случай, когда сглаживающая группа состоит из трех точек и сглаживающее значение определяется как среднее этих трех точек, т.е. по первым трем точкам , , 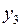получают сглаженное значение , по следующим трем точкам , , 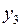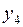получают сглаженное значение и т.д. Как правило, сглаживанию подвергается центральная точка из сглаживающей группы точек.

В общем случае формула скользящей средней для группы из 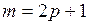точек записывается следующим образом:

(2.9)

где – значение скользящей средней для момента t ();

– фактическое значение уровня в момент i.

Расчет скользящей средней при большом числе уровне можно несколько упростить, используя рекурсивную формулу

(2.10)

в которой используется предыдущее значение сглаженного уровня.

Одним из недостатков рассматриваемого подхода принято считать то, что крайние точки временного ряда невозможно сгладить по формуле (2.9), и поэтому они исключаются из сглаженного временного ряда. Некоторые авторы решают эту проблему путем введения специальных формул для сглаживания крайних значений. Если для сглаживания по трем точкам используется формула

(2.11)

то для сглаживания левой крайней точки можно использовать выражение

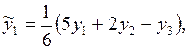(2.12)

а для сглаживания правой крайней –

(2.13)

В случае сглаживания по пяти точкам

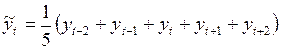(2.14)

левые крайние точки сглаживаются по формулам

(2.15)

(2.16)

а правые крайние –

(2.17)

(2.18)

Таким образом, при использовании для сглаживания временных рядов скользящей средней, можно избежать потери крайних значений, если для их сглаживания применить выше приведенные формулы.

Сглаживание с помощью скользящей средней, по сути, является линейной процедурой, и в силу этого результаты ее применения часто оказываются весьма грубыми. Более гибкое сглаживание обеспечивается нелинейной процедурой. Если в качестве сглаживающей кривой выбрать параболу, то получим процедуру сглаживания, в которой используется взвешенная скользящая средняя. Выше рассмотренная скользящая средняя является ее частным случаем.

Весовые коэффициенты взвешенной скользящей средней определяются по методу наименьших квадратов, путем минимизации выражения

(2.19)

Не умаляя общности, для упрощения проводимых ниже преобразований положим 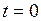(к этому случая всегда можно прийти, если от текущего индекса вычесть 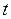), тогда (2.19) перепишется в виде

(2.20)

Так как всегда сглаживается центральное значение, т.е. значение при , то достаточно определить параметр , значению которого как раз и равен сглаживаемый уровень временного ряда. Для этого продифференцируем (2.20) по всем параметрам и полученное выражение приравняем к 0

Перенеся известные величины вправо, получаем следующую систему уравнений:

Используя специфику суммирования, приходим к системе

у которой второе уравнение не связано с первым и третьим. Поэтому параметр определяется из системы

Решим эту систему, используя метод Крамера. Для этого сначала вычислим ее определитель

а затем найдем оценку следующим образом:

(2.21)

Таким образом, для p = 2 (в сглаживании участвуют пять точек) получаем весовые коэффициенты, позволяющие взвешенную скользящую среднюю для любого записать в следующем виде:

( 2.22 )

Для случая, когда в расчете взвешенной скользящей средней используется 7 точек (p = 3), точно таким же образом получается следующая формула для расчета взвешенной скользящей средней:

( 2.23 )

Сглаженные данные предпочтительней использовать для анализа динамики, так как процедура сглаживания сводит к минимуму влияние случайной составляющей. Следовательно, такие характеристики, как средний абсолютный прирост или темп роста, будут свободны от искажения случайной компонентой.

Не нашли, что искали? Воспользуйтесь поиском: