
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решая линейную систему (3.26) с помощью замены
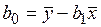
получаем оценки коэффициентов линейной трендовой модели в виде
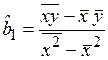 ;
; 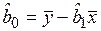 . (3.27)
. (3.27)
В случае, когда в качестве тренда выбрана нелинейная функция, возникают некоторые проблемы построения таких функций с помощью МНК. Рассмотрим все варианты, которые могут иметь место в таких случаях.
Нелинейные модели принято делить на три класса: нелинейные по независимой переменной; нелинейные по оцениваемым параметрам, но приводящиеся путем преобразования к линейному виду; нелинейные по оцениваемым параметрам и не приводящиеся к линейному виду.
Нелинейные по независимой переменной:
§ парабола 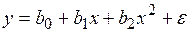 ;
;
§ полином третьей степени 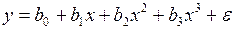 ;
;
§ равносторонняя гипербола 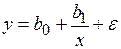 .
.
Нелинейные по оцениваемым параметрам:
· степенная 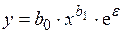 ;
;
· показательная 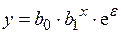 ;
;
· экспоненциальная 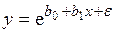 .
.
Коэффициенты моделей первого класса после замены переменных рассчитываются с помощью метода наименьших квадратов. Построение моделей второго класса требует предварительного их приведения к линейному виду путем логарифмирования
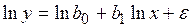 ;
;
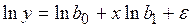 ;
;
 .
.
После построения с помощью метода наименьших квадратов преобразованных моделей коэффициенты исходных моделей в случае необходимости получаются путем потенцирования.
Модели третьего класса (логистическая модель Перла – Рида и кривая Гомперца) не приводятся к линейному виду и, следовательно, не могут быть построены с помощью МНК.
Метод трех сумм
Метод трех сумм является упрощенным методом оценивания параметров нелинейных моделей, принадлежащих третьему классу согласно классификации, проведенной в предыдущем параграфе. Применение этого метода к различным моделям привносит определенную специфику в его реализацию. Ниже рассматриваются варианты применения метода трех сумм к построению трех моделей: модифицированной экспоненте, кривой Гомперца и логистической кривой Перла – Рида.
Метод трех сумм для модифицированной экспоненты. Наиболее простой моделью, для построения которой необходимо применять метод трех сумм, является модифицированная экспонента
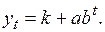 (3.28)
(3.28)
Поэтому вначале изложим вычислительную схему метода трех сумм применительно к модифицированной экспоненте.
В соответствии с этим методом весь ряд наблюдений
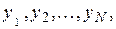
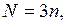
разбивается на три равных отрезка или периода по n уровней в каждом. Сумму уровней для каждого периода обозначим как 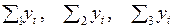 .
.
Если бы уровни ряда были в точности рассчитаны по модифицированной экспоненте, т.е.
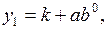
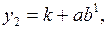
…………,
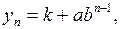
то сумма этих уровней для первого периода составила бы величину
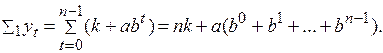 (3.29)
(3.29)
Прежде чем перейдем к определению 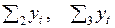 , упростим выражение (3.28). Нетрудно понять, что сумма в скобках – это геометрическая прогрессия со знаменателем
, упростим выражение (3.28). Нетрудно понять, что сумма в скобках – это геометрическая прогрессия со знаменателем 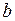 . Поэтому
. Поэтому
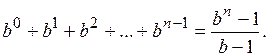
Откуда получаем, что
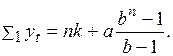 (3.30)
(3.30)
Аналогично определим две следующие суммы:
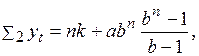 (3.31)
(3.31)
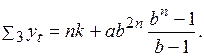 (3.32)
(3.32)
Решение системы из 3-х уравнений (3.30) – (3.32) позволяет определить три искомых параметра. Это решение получается в предположении, что суммы уровней расчетного ряда равны суммам уровней фактического ряда.
Для получения решения вычтем первое уравнение из второго и второе из третьего. Получаем
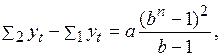 (3.33)
(3.33)
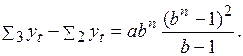 (3.34)
(3.34)
Решим эту систему относительно 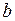 , для чего разделим (3.34) на (3.33), в итоге получим:
, для чего разделим (3.34) на (3.33), в итоге получим:
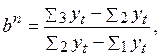
а, следовательно,
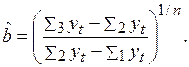 (3.35)
(3.35)
Подставляя 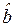 в (3.33) найдём
в (3.33) найдём
 (3.36)
(3.36)
И, наконец, из уравнения (3.30) найдём k
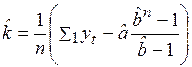 . (3.37)
. (3.37)
Таким образом, определены все параметры модифицированной экспоненты.
Заметим, что данный метод очень чувствителен к колебаниям исходных данных. Разность сумм в знаменателе при вычислении 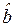 может оказаться равной нулю или быть отрицательной, и тогда
может оказаться равной нулю или быть отрицательной, и тогда 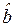 нельзя определить. Поэтому перед расчётом параметров данные необходимо подвергнуть сглаживанию.
нельзя определить. Поэтому перед расчётом параметров данные необходимо подвергнуть сглаживанию.
Метод трех сумм для кривой Гомперца. Как известно, кривая Гомперца имеет вид
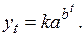 (3.38)
(3.38)
Не нашли, что искали? Воспользуйтесь поиском: