
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Обработка результатов косвенных измерений
Рассмотрим случай, когда интересующая нас величина z является функцией k непосредственно измеряемых величин x1, x2,…, xk:
| z = z (x1, x2, …, xk). | (8.4.1) |
Обозначим через x1i, x2i,…, xni набор значений, принимаемых первичными переменными при их i -м измерении. Пусть всего проведено n измерений и, соответственно, получено n таких наборов, то есть i пробегает значения от 1 до n: i = (1, n). При обработке этих результатов можно поступить двояким образом.
Способ 1
Вычисляем n значений zi функции z, подставляя в выражение (8.4.1) конкретные наборы значений аргументов x1i, x2i,…, xki:
| zi = z (x1i, x2i,…, xki), | i = (1, n). | (8.4.2) |
После этого совокупность вычисленных значений zi обрабатываем как серию прямых измерений с помощью формул (5.2.1) и (8.3.1):
· находим среднее арифметическое из этих n значений zi функции z

| (8.4.3) |
· оцениваем ошибку косвенных измерений по формуле Стьюдента (8.3.1)

| (8.4.4) |
Способ 2
По n значениям каждой из напрямую измеренных переменных x1, x2,…, xk:с помощью методики Стьюдента по формулам (5.2.1) и (8.3.1), (7.3.2), (7.4.2), (7.5.1) находим:
· средние значения аргументов <x1>, <x2>, …, <xk>;
· ошибки D x1, D x2, …, D xk. При этом для всех переменных принимаем одно и то же значение надежности p = 0.95
Конечный результат находится подстановкой найденных средних <x1>, <x2>, …, <xk> от непосредственно измеренных величин в формулу для функции z
| z = z (<x1 >, <x2 >, …, <xk >). | (8.4.5) |
Полуширину доверительного интервала D z для результата косвенных измерений оцениваем по формуле

| (8.4.6) |
где  - частные производные функции z, вычисляемые при значениях переменных x1 = <x1>, x2 = <x2>, …, xk = <xk>. Каждая частная производная может быть найдена как обыкновенная производная функции z (x1, x2, …) по соответствующему аргументу, если оставшиеся аргументы рассматривать как постоянные параметры ([5], с. 107).
- частные производные функции z, вычисляемые при значениях переменных x1 = <x1>, x2 = <x2>, …, xk = <xk>. Каждая частная производная может быть найдена как обыкновенная производная функции z (x1, x2, …) по соответствующему аргументу, если оставшиеся аргументы рассматривать как постоянные параметры ([5], с. 107).
Результирующая погрешность D z имеет ту же надежность p = 0.95.
Сравнивая слагаемые в подкоренном выражении (8.4.6), можно понять, погрешности каких из непосредственно измеряемых величин вносят наибольший вклад в окончательную ошибку D z. Указанный анализ выражения (8.4.6) для результирующей ошибки D z полезен для того, чтобы при подготовке и проведении эксперимента направить основные усилия на повышение точности в определении тех параметров, которые вносят основной вклад в ошибку D z и, напротив, увидеть, на измерения каких величин можно не затрачивать большого труда.
В качестве примера применения второго способа рассмотрим обработку косвенных измерений величины z по измерениям двух величин - x и y: z = z (x, y). Среднее значение <z> находим по средним <x> и <y>
| <z> = z (<x>, <y>), | (8.4.7) |
а для вычисления погрешности D z воспользуемся правилом (8.4.6)

| (8.4.8) |
где D x и D y – погрешности в определении величин x и y.
Пусть, например, в нашей задаче об определении расстояния шагами (параграф 8.1) требовалось определить не число шагов X от дома до работы, а расстояние L в метрах. Тогда необходимо было бы еще измерить среднюю длину шага l на некоторой мерной длине, например, на стометровке. Пусть в результате этих дополнительных измерений оказалось, что длина шага l равна
| l = (0.99 ± 0.02) м | (p = 0.95). | (8.4.9) |
Тогда среднее расстояние от дома до работы <L> = <x> ∙ <l> равнялось бы
<L> = <x> ∙ <l> = 6.4∙103∙0.99  6.3∙103 м. 6.3∙103 м.
| (8.4.10) |
Для того, чтобы оценить погрешность опыта, учтем, что в нашем случае формула (8.4.8) приводит к следующему выражению:

| (8.4.11) |
которое удобно записать, разделив обе части на <L>2 = <x>2 ∙ <l>2:
  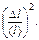
| (8.4.12) |
Отсюда можно найти погрешность
  
| (8.4.13) |
Разрешая это уравнение относительно D L, находим D L  2∙102 м. Таким образом, окончательный результат должен быть записан так:
2∙102 м. Таким образом, окончательный результат должен быть записан так:
| L = (6.3 ± 0.2)∙103 м | (p = 0.95). | (8.4.14) |
Более подробные сведения по статистической обработке данных можно найти в книгах [1] и [6]. В них показано, в частности, что, если ошибки измерений малы по сравнению с измеряемой величиной, то оба приведенных выше способа обработки результатов косвенных измерений дают одинаковые данные. Однако с точки зрения удобства расчетов второй способ представляется менее трудоемким.
Не нашли, что искали? Воспользуйтесь поиском: