Атты денелердің айналмалы қозғалысы 4 страница

2.92. Нейтрон (массасы 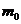) көміртегі атомының қозғалмайтын ядросына келіп соғылады 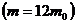.Соғылысуды центрлік және серпімді деп алып, соғылысу уақытында нейтронның кинетикалық энергиясының неше есе кемитіндігін табу керек.

2.93. Нейтрон (массасы 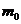) қозғалмайтын: 1) көміртегі атомының 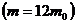, 2) уран атомының 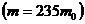ядросына келіп соғылады. Соғылысуды центрлік және серпімді деп алып, соғылысу уақытында нейтрон өзінің жылдамдығының қандай бөлігін жоғалтатынын табу керек.

2.94. Жердің өз осінен айналу салдарынан экватордағы дененің салмағы өз салмағының қандай бөлігіне кемиді?

2.95. Экватордағы дененің салмағы болмау үшін Жер бетіндегі тәуліктің ұзақтығы қандай болу керек?

2.96. Массасы 5 т трамвай вагоны радиусы 128 м бұрылыспен жүріп келеді. Қозғалыс жылдамдығы 9 км/сағ болғанда дөңгелектің рельске түсіретін бүйірлік қысым уүшін табу керек?

2.97. Ұзындығы 60 см жіпке байланған суы бар шелек вертикаль жазықтықта бір қалыпты айналады. Мыналарды: 1)шелек ең жоғары нүктеге жеткен уақытта оның ішіндегі су төгілмейтін ең кіші айналу жылдамдығын, 2)осы жылдамдықтардағы шеңбердің ең жоғарғы және ең төменгі нүктелеріндегі жіптің керілуін табу керек. Шелектің сумен бірге есептегендегі массасы 2 кг-ға ең.

2.98. Ұзындығы см жіпке байланған тас вертикаль жазықтықта бір қалыпты айналады. Жіпке тастың он еселенген салмағына тең жүк тиегенде үзіледі деп алып, секундтың қандай айналым санында жіптің үзілетіндігін табу керек.

2.99. Жіпке байланған тас вертикаль жазықтықта бір қалыпты айналады. Жіптің максимал және минимал керілулерінің айырымы 1 кГ-ға тең деп, тастың массасын табу керек.

2.100. Ұзындығы 30 см жіпке ілінген кішкене гир горизонталь жазықтықта радиусы 15 см-ге тең шеңбер сызады. Гирдің айналу жылдамдығы бір минуттағы қандай айналым санына сәйкес келеді?

2.101. Ұзындығы 25 см жіпке байланған, массасы 50 г кішкентай гир горизонталь жазықтықта 2 айн/сек-қа сәйкес келеді. Жіптің керілуін табу керек.

2.102. Вертикаль осьті айналған дискі 30 айн/мин жасайды. Дискінің үстінде айналу осьтен 20 см қашықтықта дене қойылған. Дене дикінің үстімен сырғанап түсіп қалмау үшін дене мен дискінің арасындағы үйкеліс коэффициенті қандай болу керек?

2.103. 900 км/сек жылдамдықпен ұшқан самолет «өлі тұзақ» жасайды. Ұшқышты отарған орындығына қысатын ең үлкен күш: 1)ұшқыштың бес есе салмағына, 2)ұшқыштың он есе салмағына тең болу үшін «өлі тұзақтың» радиусы қандай болу керек?

2.104. 72 км/сағ жылдамдықпен горизонталь жолмен жүріп келе жатқан мотоциклист қисықтық радиусы 100 м болатын жолмен бұрылады. Бұрылған уақытта құлап кетпеу үшін мотоциклист қаншама қисаю керек?

2.105. Трамвай вагонының төбесіне жіпке байланған шар ілінген. Радиусы 36,4 м бұрылыспен жүріп келе жатқан вагонның жылдамдығы 9 км/сағ. Осы уақыттағы шар байланған жіптің бұрылу бұрышы қандай болады?

2.106. Центрден тепкіш регулятор (4 сурет) стерженьдерінің ұзындығы 12,5 см-ге тең. Егер стерженьге кигізген жүктер айналғанда вертикальдан: 1) 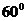, 2) 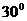бұрышқа ауытқыған болса, онда центрден тепкіш регулятор бір секундта қанша айналым жасар еді?

2.107. Жолдың бұрылыс қисықтығының 100 м радиусында шоссе виражы кеңістікпен 10⁰ бұрыш жасайды.Вираж қандай жылдамдыққа есептелген?

2.108. Жіпке ілінулі тұрған салмағы 1 кГ жүк 30⁰бұрышқа ауытқиды.Жүктің тепе-тепе теңдік қалыптан өткен моментінденгі жіптің керілуін табу керек.

2.109. Бала «алып адымда» («гигантский шаг»)16 айн/мин жасай айналады.Арқанның ұзындығы 5 м -ге тең. «Алып адымда» арқандары мен вертикаль арасындағы бұрыш қандай? 2) Егер баланың салмағы 45 кГ –ға тең десек, онда арқанның керілуі қандай болады? 3) Баланың сызықтық айналу жылдамдығы қандай?

2.110. Ұзындығы m=0.5м салмақсыз стерженьге ілінген массасы l= 1 кг жүк вертикаль жазықтықта тербеледі. 1) Стерженьнің вертикальдан қандай бұрышқа бұрылғандығы жүктің алатын ең төменгі қалпында оның кинетикалық энергиясы W=2.45 дж- ға тең болады? 2)Осы бұрылу бұрышындағы стерженьнің орталық қалыптағы керілуінен неше есе артық болады?

2.111. Салмақсыздық стерженьге Р жүк ілінген. Жүктің 90⁰ бұрышқа бұрып, қайтадан босатып жіберді.Тепе-теңдік қалыптан өткен уақыттағы стерженьнің керілуін табу керек.

2.112. Белгілі бір радиусты болат сым 300кГ-ға дейінгі жүкті көтеруге шыдайды.осындай сымға ілінген жүктің массасы 150 кг. Жүк тепе-теңдік қалыптан өткен уақытта жүк ілінген сым үзіліп кетпес үшін, оны қанай ең үлкен бұрышқа бұру керек?

2.113. Ұзындығы l= 50 см жіпке байланған, сымға 0,5 кГ тас вертикаль жазықтықта бір қалыпты айналады.Шеңбердің ең төменгі нүктесіндегі жіптің керілуі Т= 44 н -ға тең. Егер тасты жылдамдығы вертикаль жоғары бағытталған моментте үзіледі десек,онда ол қандай биіктікке көтерілетін болады?

2.114. Радиусы R=20,0 м горизонталь жазықтықта жатқан труба арқылы су ағады. Центірден тепкіш күштің әсерінен пада болған судың бүйірлік қысымын табу керек. Трубаның диаметірі d=20 см. Трубаның көлденең қимасынан бір сағат уақыт ішінде M=300 т су ағып өтеді.

2.115. Ені 0,5 м, қисықтық радиусы 10 м,горизонталь жазықтықта жатқан канал арқылы су ағады. Судың ағынының жылдамдығы 5 м/сек. Центірден тепкіш күштің әсерінен пада болатын судың бүйірлік қысымын табу керек.

2.116. Егер күш деформацияға пропорциянал болып және 29,4 н күштің әсерінен серіппе 1 см- ге қысылады десек, онда серіппені 20 см -ге қысу үшін қандай жұмыс жасау керек болады?

2.117. Рессордың, оның ортасына қойылған жүктің әсерінен болатын ең үлкен майысу шамасын табу керек. Сол жүктің әсерінен болатын рессордың статистикалық майысуы х₀=2 см. Егер сол жүк рессордың ортасына h=1м биіктіктен бастапқы жылдамдықсыз түсетін болса, онда оның ең үлкен бастапқы майысуы қандай болады?

2.118. Акробат торға Н₁=8 м биіктіктен секіріп түседі. Акробат секірген кезде еденге соғылмау үшін, торды еденнің үстінен қандай шекті биіктіктен һ₁ керіп қою керек болады? Ал егер акробат торға H₂=1 м биіктіктен секіріп тісетін болса, онда тордың керілуінің биіктігі h₂=0,5 м болатыны белгілі.

2.119. Таразының табағына жүк салынған.Егер таразы табақтарының шайқалуы тоқталғаннан кейін стрелка 5 бөлікті көрсететін болса, онда жүкті алғаш салған сездегі серпілуде таразының стрелкасы қандай бөлікті көрсетеді?

2.120. Таразының табағына 10 см биіктіктен салмағы 1 кГ жүк құлап түседі. Жүктің табаққа соғылған моментіндегі таразының көрсетуі қандай болады? Осы жүктің әсерінен таразы тынышталғаннан кейін оның табағы 0,5 см төмен түсетіні белгілі.

2.121. Егер қабырғаға соққы түскенде әрбір буфер 10 см қысылатын болса,онда массасы 20 т вагон қандай жылдамдықпен қозғалатын болады? Әрбір буфердің пружинасы 1 т күштің әсерінен 1 см -ге қысылатындығы белгілі.

2.122. Бала рогатканы атарда, оның резеңке жібінің ұзындығы 10 см -ден артық болатындай етіп тартып созды. Массасы 20 г тас қандай жылдамдықпен ұшты. Резеңке жіпті 1 см -ге тартып ұзарту үшін 1 кГ күш керек болды. Тас ұшқан кезде ауаның кедергісі ескерілмейді.

2.123. Вертиккаль ілінген серіппенің төменгі ұшына, бір ұшына жүк бекітілген екінші бір серіппе жалғастырылған. Серіппелердің деформация коэффициенттері сәйкес R₁ және R₂ -ге тең. Жүктің салмағына қарағанда серіппелердің салмағы жоқтың қасында деп есептеп, осы серіппелердің потенциялдық энергиялардың өз ара қатынасын табу керек.

2.124. Ұзындықтары бірдей екі параллель серіппеге салмақтарын ескермуге болатындай стержень ілінген. Серіппелердің коэффиценттері сәйкес R₁ =2 кГ/см және R₂ = 3 кГ/см -ге тең. Стерженьнің ұзындығы серіппелердің L =10 см араларындағы қашықтығына тең. Стержень горизолнталь қалпын сақтап қалу үшін жүкті стерженьнің қай жеріне ілу керек?

2.125. Горизонталь бағытта кейбір жылдамдықпен ұшып келе жатқан массасы m=0,1кг резеңке доп қозғалмайтын вертикаль қабырғаға келіп соғылады. 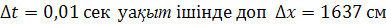-ге қысылады; доптың алғашқы формасына қайтадан келу үшін де осындай 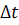уақыт кетеді. Доптың қабырғаға соғылған уақытындағы қабырғаға әсер ететін орташа күшті табу керек.

2.126. Ұзындығы l₀ резеңке жіпке байланған салмағы Р=4,9 н гир горизонталь жазықтықта шеңбер сызады. Гирдің айналу жылдамдығы

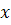айн/сек жиілікке сәйкес келеді.Резеңке жіптің вертикаль бағыттан ауытқу бұрышы 30⁰-қа тең. Созылмаған резеңке жіптің ұзындығын ₀ табу керек. Жіпті ₁ 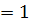см- ге созу үшін ₁ 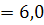н күш керек болады.

2.127. Ұзындығы ₀ 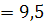см резеңке жіпке байланған салмағы Р 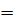0,5 кГ жүкті 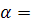90⁰ бұрышқа бұрып, содан кейін босатып жіберді. Жүктің тепе-теңдік қалыптан өткен моменттегі резеңке жіптің ұзындығын табу керек. Резеңке жіптің деформация коэфиценті R = 1 кГ/см – ге тең.

2.128. Радиусы R = 10 см доп, оның центірі судың бетінен Н = 9 см жоғары шығып тұратындай, су жүргізіп жүреді. Допты судың ішіне диаметриялық жазықтыққа дейін батыру үшін қандай жұмыс істеледі?

2.129. Радиусы R = 6 см шар сыртқы күштің әсерімен, оның жоғарғы нүктесі судың бетіне тиіп тұратындай, судың астында ұсталып тұр. Шар заттың тығыздығы р = 500 кг/м³. Егер шарды босатып, оған өз еркімен жүзуге мүмкіншілік берсек, онда ығыстырушы күштің істейтінжұмыс қандай болады?

2.130. Суда жүзіп жүрген шардың диаметірі D=30 см. Шарды одан әрі h=5 см тереңдікке батыру үшін қандай жұмыс істеу керек? Шар материалының тығыздығы p=500кг/м³.

2.131. Суда жүзіп жүрген мұздың көлденең қимасының ауданы S=1 м² және биіктігі Н=0,4 м. Мұзды суға түгелімен батыру үшін қандай жұмыс істеу керек?

2.132. Бір-бірінен r =10^-10м қашықтықта тұрған екі протонның тартылу күшін табу керек. Протон ның мсассасы т=1,67 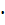10^-27кг. Протондарды нүктелік масса деп есептеу керек.

2.133. Бір-біріне тиіп тұрған екі мыс шариктердің диаметірлері d₁=4 см және d₂=6 см. Осы системаның гравитациялық потенциялдық энергиясын табу керек.

2.134. Жер шарының радиусын R, орташа тығыздығын р және Жер бетіне жақын жердегі ауырлық күшінің үдеуін g деп алып, тартылыс тұрақтысын есептеп шығару керек (қосымшадағы таблицаны қараңыздар).

2.135. Жердің бетіне жақын жердегі ауырлық күшінің үдеуін g =9,80 м/сек² деп алып және III қосымшадағы белгілерді пайдаланып, Күн системасы планеталарының орташа тығыздығының таблицасын құру керек.

2.136. Космостық ракета Айға ұшып бара жатыр. Ай мен Жердің центірін қосатын түзудің қай нүктесінде ракета бірдей күшпен Айға және Жерге тартылады.

2.137. Айдың бетіндегі ауырлық күштің үдеуін Жердің бетіндегіауырлық күштің үдеуімен салыстыру керек.

2.138. Математикалық маятниктің тербеліс периоды оны Жердің бетінен Айдың бетіне көшірген уақытта қалай өзгереді?

Н ұ с қ а у. Математикалық маятниктің тербеліс периодының формуласы 12-параграфт көрсетілген.

2.139. Бірінші космостық жылдамдықтың, яғни бағыты Жер бетіне горизонталь болып келген денеге әсер еткенде дене Жердің маңында оның серігі сияқты дөңгелек орбитамен айнала алатын жылдамдықтың сан мәнін табу керек.

2.140. Екінші космостық жылдамдықтың, яғни жер бетіндегі дене берілген жылдамдықтың әсерінен Жердің тарту күшін жеңіп, содан кейін жерден мүлдем алыстап кететіндей жылдамдықтың сан мәнін табу керек.

2.141. Жер бетіндегі ауырлық күштің үдеуін g =980 см/сек² деп алып III қосымшадағы таблицаның мәліметтерін пайдалана отырып, Күн системасындағы планеталардың бетіндегі бірінші және екіші космостық жылдамдықтардың (км/сек есебімен) мәндерінің таблицасын құру керек.

2.142. Жердің орбитасын дөңгелек деп алып, оның орбита бойымен қозғалғандағы сызықтық жылдамдығын табу керек.

2.143. Дөңгелек орбитамен қозғалған Жердің жасанды спутнигінің: 1) Жер бетінде жақын жердегі (ауның кедергісін ескермейміз), 2) һ₁=200 км және һ₂=7000 км биіктіктерде 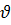сызықтық жылдамдығы қандай болады? Осы барілгендер бойынша Жердің жасанды спутнигінің айналу периодын Т табу керек.

2.144. 1) Центірлік дененің бетінде айналып жүрген жасанды спутниктің айналып шығу периодының, осы дененің орташа тығыздығына қандай тәуелділікте болатындығын табу керек. 2) 2.135. есепті шығарғанда алынған нәтижелерді пайдаланып, Күн системасындағы планеталарды дөңгелек орбитамен айналатын жасанды спутниктердің айналып шығу периодтарының таблицасын құру керек.

2.145. Жер бетінен 200 км биіктікте дөңгелек орбитамен айналып жүрген Жердің жасанды спутнигінің центірге тартқыш үдеуін табу керек.

2.146. Марс планетасының Фобос және Деймос деп аталатын екі серігі бар. Біріншісінің Марстың центірінен қашықтықтағы R₁ =9500 км, ал екіншісінің – R₂ =24000 км. Осы жасанды спутниктердің Марсты айналып шығу периодын табу керек.

2.147. Жердің жасанды спутнигі экватор жазықтығындағы дөңгелек орбитамен батыстан шығысқа қарай айналады. Жердің бетінде бақылап тұрған адамға қозғалмайтын болып көріну үшін, осы жасанды спутник Жерден қандай қашықтықта тұру керек?

2.148. Айдың жасанды спутнигі Ай бетінен 20 км қашықтықта дөңгелек орбитаның бойымен қозғалады. Осы жасанды спутниктің сызықтық жылдамдығын және оның Айды айналып шығу периодын табу керек.

2.149. Айға деген бірінші және екінші космостық жылдамдықтың сан мәнін табу керек (2.139. және 2.140 есептердің шығарылу шартын қарастырыңыздар).

2.150. Ауырлық күш үдеуінің Жер бетінен алғандағы биіктікке тәуелділігін табу керек. Жер бетінен қандай биіктікте ауырлық күштің үдеуі Жер бетіндегі ауырлық күш үдеуінің 25 процентін құрады?

2.151. Жер бетінен қандай қашықтықта ауырлық күштің үдеуі 1 м/сек-ке тең болады?

2.152. Дөңгелек орбита бойымен қозғалған Жердің жасанды спутнигінің кинетикалық энергиясы оның гравитациялық потенциялдық энергиясынан қанша есе артық болады?

2.153. Денені һ тереңдікке түсіргендегі ауырлық күш үдеуінің өзгерісін табу керек. Қандай тереңдікте ауырлық күш үдеуі Жер бетіндегі ауырлық күш үдеуінің 25 процентін құрады? Жердің тығыздығын тұрақты деп есептейміз.

Н ұ с қ а у. Жер бетінен һ тереңдікте жатқан дене өзінің үстіндегі һ қалыңдықтағы шар қабатының ешқандай тарту әсерін сезбейтіндігі ескеру керек. Өйткені қабаттардың жекеленген бөліктерінің тартылысы өз ара компенсацияланады.

2.154. Егер маятниктің тербелу периоды таудың төбесі және шахтаның түбінде бірдей болса, онда таудың биіктігі мен шахтаның һ тереңдігінің арасындағы қатынас қандай болады?

Н ұ с қ а у. Маятниктің тербелу периодының формуласы 12- параграфта берілген.

2.155. Советтік жасанды планетаның эллипстік үлкен жарты осінің Жер орбитасының жарты осінен 24 миллион километрге артық екендігін біле отырып, оның Күнді айналып шығу периодын табу керек.

2.156. Советтік жасанды планетаның орбитасы дөңгелек орбитаға шамалас. Планетаның орбитасы дөңгелек деп есептеп, оның қозғалысының сызықтық жылдамдығын және оның қозғалысының сызықтық жылдамдығын және оның Күнді айналып шығу периодын табу керек. Күннің диаметірін және оның тығыздығын белгілі деп алмыз. Планетаның Күннен орташа қашықтығы R =1,71 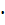10⁸ км.

2.157. Дүние жүзіндегі Жердің бірінші жасанды спутнигінің орбитасының үлкен осі Жердің екінші жасанды спутнигі орбитасының үлкен осінен 800 км кіші. Бірінші жасанды спутниктің қозғала бастағандағы Жерді айналып шығу периоды 96,2 мин-қа тең болады. Мыналарды: 1) Жердің екінші жасанды спутнигінің орбитасының үлкен осінің шамасын, 2) оның Жерді айналып шығу периодын табу керек.

2.158. Космостық корабль-спутник «Восток 2» - нің Жердің бетінен минимал қашықтауы 183 км, ал максимал қашықтауы 244 км болады. Космостық корабльдің Жерді айналып шығу периодын табу керек.

2.159. Радиусы r- ға тең жіңішке сымнан жасалған сақина берілген. Сақина осінің үстінде оның центірінен L қашықтықта жатқан массасы m материялық нүктені, осы сақинаның қандай күшпен өзіне тартатындығын табу керек. Сақинаның радиусы R, сым затының тығыздығы р -ға тең.

2.160. Радиусы 1 мм-ге тең жіңішке мыс сақина берілген. Сақинаның радиусы 20 см-ге тең. 1) осы сақинаның F күшпен сақина осінің үстінде, оның центірінен 0, 5, 10, 15, 20 және 50 см қашықтықта жатқан массасы 2 г материялық нүктені өзіне қалай тартатаын табу керек. F мәнінің таблицасын құрып, F=f (L) тәуелділігінің графигін сызу керек. 2) сақинаның қандай қашықтығында сақина мен материялық нүктенің арасындағы өз ара әсер етуші күш максимал болады? 3) сақина мен материялық нүктенің арасындағы өз ара әсер етуші максимал күштің сан мәнін табу керек.

2.161. Сымнан жасалынған сақина мен оның осінің үстінде жатқан материялық нүктенің өз ара әсер күшінің F максимал мәні, нүкте сақинаның центірінен L_max қашықтықта жатқанда болады. Сақина мен сақинаның центірінен L=0,5 L_max қашықтықта жатқан материялық нүктелердің өз ара әсер күші максимал күштен қанша есе кем болады?

атты денелердің айналмалы қозғалысы

Қандай болмасын, айналу осімен салыстырғандағы F күштің M моменті төмендегі формуламен анықталады:

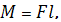
Мұндағы - айналу осінен бойымен күш әсер ететін түзуге дейінгі қа- шықтық.

Материялық нүктенің қандай болмасын айналу осіне қатысты инерция моменті деп мына шаманы айтамыз:

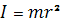
мұндағы - материялық нүктенің массасы, ал 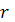– нүктенің осьтен қашық-

тығы.

Қатты дененің оның айналу осі арқылы алынған инерция моменті

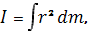
мұнда интегралдауды дененің барлық көлемі арқылы жүргізу керек. Интегралдау жүргізе отырып мынадай формулалар алуға болады:

1) өзінің осі арқылы алынған тұтас біртекті цилиндрдің (дискінің) инерция моменті

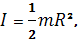
Не нашли, что искали? Воспользуйтесь поиском: