
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Газдар мен сұйықтардың механикасы
Сығылмайтын идеал сұйықтың қалыптасқан қозғалысы үшін Бернулли теңдеуі алынады.

Мұндағы р — сұйықтың тығыздығы, v — трубаның берілген қимасындағы сұйық қозғалысының жылдамдығы, h — трубаның берілген қимасының кейбір деңгейден алынған биіктігі және р — қысым. Бернуллидің теңдеуінен, кішкентай тесіктен сұйықтың ағып шығу жылдамдығы  мұндағы һ — тесіктен жоғары қарай алынған сұйықтың бетіне дейінгі биіктік. Қандайда болмасын трубаның көлденең қимасынан бірдей көлемдегі сұйық өтетін болғандықтан,
мұндағы һ — тесіктен жоғары қарай алынған сұйықтың бетіне дейінгі биіктік. Қандайда болмасын трубаның көлденең қимасынан бірдей көлемдегі сұйық өтетін болғандықтан,  болады, мұндағы v1 және v2 — көлденең қималарының ауданы S1 және S2 трубаның екі қимасынан өтетін сұйықтардың жылдамдығы.
болады, мұндағы v1 және v2 — көлденең қималарының ауданы S1 және S2 трубаның екі қимасынан өтетін сұйықтардың жылдамдығы.
Тұтқыр сұйықта (немесе газда) құлайтын шарикке жасалатын кедергі күш Стокс формуласымен анықталады:

мұндағы  — сұйықтың немесе газдың ішкі кедергісінің коэффициенті (динамикалық тұтқырлық), r — шариктің радиусы, v — оның жылдамдығы. Стокстың заңы тек қана ламинарлық қозғалыс үшін берілген. Ламинарлық қозғалыс кезінде t уақыт ішінде радиусы r және ұзындығы t капилляр түтік арқылы ағып өтетін сұйықтың (газдың) көлемі Пуазейль формуласымен анықталады
— сұйықтың немесе газдың ішкі кедергісінің коэффициенті (динамикалық тұтқырлық), r — шариктің радиусы, v — оның жылдамдығы. Стокстың заңы тек қана ламинарлық қозғалыс үшін берілген. Ламинарлық қозғалыс кезінде t уақыт ішінде радиусы r және ұзындығы t капилляр түтік арқылы ағып өтетін сұйықтың (газдың) көлемі Пуазейль формуласымен анықталады
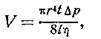
мұндағы  — сұйықтың (газдың) динамикалық тұтқырлығы,
— сұйықтың (газдың) динамикалық тұтқырлығы,  — түтік ұштарындағы қысымдардың айырымы. Сұйық (газ) қозғалысының сипаты Рейнольдстің өлшемсіз саны арқылы анықталады
— түтік ұштарындағы қысымдардың айырымы. Сұйық (газ) қозғалысының сипаты Рейнольдстің өлшемсіз саны арқылы анықталады

мұндағы D — сұйықтықпен (газбен) ағатын дененің сызықтық мөлшерін сипаттайтын шама, v — сұйықтың ағу жылдамдығы, р — тығыздық,  — динамикалық тұтқырлық. Қатынас
— динамикалық тұтқырлық. Қатынас 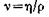 кинематикалық тұтқырлық деп
кинематикалық тұтқырлық деп
аталады.
Ламинарлық қозғалыстан турбулентті қозғалысқа ауысуды анықтайтын Рейнольдс санының кризистік мәні әр түрлі формалы денелерде түрліше болады.
4.1. Трубаның көлденең қимасынан жарты сағат ішінде 0,51 кГ көмір қышқыл газы ағып өтеді деп, осы газдың трубадан ағу жылдамдығын табу керек. Газдың тығыздығын 7,5 кг/м3 деп аламыз. Трубаның диаметрі 2 см-ге тең.
4.2. Цилиндр формалы ыдыстың түбінде, диаметрі d—1см дөңгелек тесік бар. Ыдыстың диаметрі D = 0,5. Ыдыстың ішіндегі су деңгейінің төмендеу жылдамдығының осы деңгейдің һ биіктігіне тәуелділігін табу керек. Биіктік h = 0,2 м деп, осы жылдамдықтың сан мәнін табу керек.
 4.3. Стол үстінде тұрған ішінде суы бар ыдыстың бүйір бетіндегі кішкене тесік ыдыстың түбінен h1 қашықтықта, ал судың деңгейінен h2 қашықтықта орналасқан. Ыдыстың ішіндегі судың деңгейі тұрақты. Тесіктен шапшып аққан су (горизонталь бойында) столдың үстіне қандай қашықтыққа түседі? Есепті мынадай жағдайлар үшін: 1) h1 =25 см және h2 =16 см, 2) h1 = 16 см және h2 = 25 см шешіңіздер.
4.3. Стол үстінде тұрған ішінде суы бар ыдыстың бүйір бетіндегі кішкене тесік ыдыстың түбінен h1 қашықтықта, ал судың деңгейінен h2 қашықтықта орналасқан. Ыдыстың ішіндегі судың деңгейі тұрақты. Тесіктен шапшып аққан су (горизонталь бойында) столдың үстіне қандай қашықтыққа түседі? Есепті мынадай жағдайлар үшін: 1) h1 =25 см және h2 =16 см, 2) h1 = 16 см және h2 = 25 см шешіңіздер.
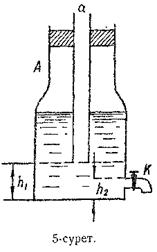
4.4. Су толтырылған А ыдыс (Мариотт ыдысы), оның мойнынa жабыстырылған шыны түтік арқылы атмосферамен қатысты жасалған (5-сурет). К краны ыдыстың түбінен h2 = 2 см қашықтықта орналасқан. Түтіктің төменгі ұшы мен ыдыс түбінің араларының қашықтығын: 1) h1 = 2 см, 2) h1 = 7,5 см және 3) h1 = 10 см деп алып, судың К кранынан ағып шығу жылдамдығын табу керек.
4.5. Биіктігі h = 1 м цилиндр бак ернеуіне дейін сумен толтырылған: 1) Бактың түбіне жақын жатқан тесіктен су қанша уақытта түгел ағып шығады? Тесіктің көлденең қимасының ауданы, бактың көлденең қимасының ауданынан 400 есе кіші. 2) Бактағы судың деңгейі үнемі h =1 л биіктікте ұстап тұрғандағы судың тесіктен ағып шығуына кететін уақытын жоғарыдағы табылған уақытпен салыстырыңыздар.
4.6. Ыдысқа су құйылып тұр, ал 1 сек ішінде құйылған судың мөлшері 0,2 л. Ыдыстың ішіндегі суды h = 8,3 см-ге тең тұрақты деңгейге тұру үшін ыдыстың түбіндегі тесіктің диаметрі d қандай болу керек?
4.7. Бояуыш пульттің ішінен ағып шығатын сұйық бояудың жылдамдығы 25 м/сек-қа тең болса, онда бояуыш пульттегі компрессордың жасайтын қысымы қандай болады? Бояудың тығыздығы 0,8 г/см3-ге тең.
4.8. Сұйық горизонталь АВ (6-сурет) трубасы арқылы ағады. Осы сұйықтың а және b трубалардағы деңгейлерінің
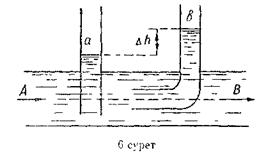
айырымы 10 см-ге тең а және b трубаларының диаметрлері бірдей. АВ трубадағы сұйықтың ағатын жылдамдығын табу керек.
4.9. АВ трубасы арқылы ауа үрленіп тұр (7-сурет). Әрбір минут сайын АВ трубасы арқылы 15 л ауа өтеді.

АВ трубаның жуан бөлігінің көлденең қимасы 2 см2-ге тең, ал оның жіңішке бөлігінің және аbс трубасының көлденең қимасы 0,5 см2-ге тең. abc трубасына құйылған судың деңгейлерінің айырымын 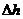 табу керек. Ауаның тығыздығын 1,32 км/м3-ге тең деп аламыз.
табу керек. Ауаның тығыздығын 1,32 км/м3-ге тең деп аламыз.
4.10. Тығыздығы шарик материалының тығыздығынан 4 есе артық сұйық ішіндегі шарик тұрақты жылдамдықпен қалқып шығады. Қалқып шығатын шарикке әсер ететін үйкеліс күші осы шариктің салмағынан неше есе үлкен болады?
4.11. Егер ауаның динамикалық тұтқырлығы 1,2 ∙ 10-4 г/см ∙ сек-қа тең болса, онда диаметрі d = 0,3 мм жаңбыр тамшысы ең үлкен жылдамдыққа қалай жететін болады?
4.12. Диаметрі 1 мм болат шарик кастор майы толтырылған үлкен ыдыстың ішіне 0,185 см/сек тұрақты жылдамдықпен түседі. Кастор майының динамикалық тұтқырлығын табу керек.
4.13. Диаметрлері 3 мм және 1 мм қорғасын пытыраларды араластырып, тереңдігі 1 м глицерин құйылған бакқа тастайды. Диаметрлері үлкен пытыраларға қарағанда диаметрі кіші пытыралардың ыдыс түбіне қанша уақыт кейін түсетінін табу керек? Тәжірибе температурасы кезіндегі динамикалық тұтқырлық 14,7 г/см ∙ сек.
4.14. Кастор майы толтырылған ыдыс ішінде радиусы 5 мм тығын шарик қалқып жүр. Егер шарик 3,5 м/сек тұрақты жылдамдықпен қалқитын болса, онда тәжірибе жағдайында кастор майының динамикалық және кинематикалық тұтқырлығы неге тең болады?.
4.15. Радиусы R = 2 см цилиндр формалы ыдыстың бүйір бетіне ішкі радиусы r = 1 cм, ұзындығы t =2 см горизонталь капилляр қойылған. Осы ыдысқа динамикалық тұтқырлығы  = 12 г/см ∙ сек-қа тең кастор майы құйылған. Цилиндр формалы ыдыстағы кастор майының деңгейінің төмендеу v жылдамдығының осы деңгейдің капиллярдан жоғары жатқан Н биіктікке тәуелділігін табу керек. Н = 26 см болғандағы осы жылдамдықтың сан мәнін табу керек.
= 12 г/см ∙ сек-қа тең кастор майы құйылған. Цилиндр формалы ыдыстағы кастор майының деңгейінің төмендеу v жылдамдығының осы деңгейдің капиллярдан жоғары жатқан Н биіктікке тәуелділігін табу керек. Н = 26 см болғандағы осы жылдамдықтың сан мәнін табу керек.
4.16. Ыдыстың бүйір бетіне ішкі радиусы r = 1 мм және ұзындығы l = 1,5 см горизонталь капилляр қондырылған. Ыдысқа, тәжірибе жағдайында динамикалық тұтқырлығы  = 1,0 н • сек/м2 глицерин қойылған. Ыдыстағы глицериннің деңгейі капиллярдан h = 0,18 м биіктікте өзгеріссіз сақталып тұрады. Капилляр арқылы 5 см3 глицерин ағып шығу үшін қанша уақыт керек болады?
= 1,0 н • сек/м2 глицерин қойылған. Ыдыстағы глицериннің деңгейі капиллярдан h = 0,18 м биіктікте өзгеріссіз сақталып тұрады. Капилляр арқылы 5 см3 глицерин ағып шығу үшін қанша уақыт керек болады?
4.17. Столдың үстінде тұрған ыдыстың бүйір бетіне оның түбінен h1 —5 см биіктікте горизонталь етіп капилляр қондырылған. Капиллярдың ішкі радиусы ұзындығы r = 1 мм, ал ұзындығы l = 1 см. Ыдысқа құйылған машина майының тығыздығы р = 900 кг/м3, ал динамикалық тұтқырлығы  = 0,5 н • сек/,м2. Ыдыстағы майдың деңгейі капиллярдан жоғары h2 = 50 см. биіктікте өзгеріссіз сақталып тұрады. Шапшып шыққан май столдың үстіне капиллярдың ұшынан (горизонталь бағытпен) қандай қашықтыққа түседі?
= 0,5 н • сек/,м2. Ыдыстағы майдың деңгейі капиллярдан жоғары h2 = 50 см. биіктікте өзгеріссіз сақталып тұрады. Шапшып шыққан май столдың үстіне капиллярдың ұшынан (горизонталь бағытпен) қандай қашықтыққа түседі?
4.18. Тығыздығы р = 900 кг/м3, динамикалық тұтқырлығы  = 0,8 н • сек/м2 трансформатор майымен толтырылған кең ыдыстың ішіне болат шаригі түседі. Стокстың заңы Re
= 0,8 н • сек/м2 трансформатор майымен толтырылған кең ыдыстың ішіне болат шаригі түседі. Стокстың заңы Re 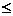 0,5 болғанда (егер Re-нi есептеп тапқанда D шаманың орнына шариктің диаметрін алатын болсақ) орындалады деп алып, шариктің диаметрінің шекті мәнін табу керек.
0,5 болғанда (егер Re-нi есептеп тапқанда D шаманың орнына шариктің диаметрін алатын болсақ) орындалады деп алып, шариктің диаметрінің шекті мәнін табу керек.
4.19. Цилиндр формалы трубадағы сұйықтың (немесе газдың) ламинарлық қозғалысы, Re 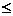 3000 болғанда сақталады деп алып (егер Re есептегенде D шаманың орнына шариктің диаметрін алу керек болса), есептің шартының ламинарлық қозғалысқа сәйкес келетіндігін көрсету керек.
3000 болғанда сақталады деп алып (егер Re есептегенде D шаманың орнына шариктің диаметрін алу керек болса), есептің шартының ламинарлық қозғалысқа сәйкес келетіндігін көрсету керек.
Газдың кинематикалық тұтқырлығын v = 1,33 Х 10-6 м2/сек-қа тең деп есептейміз.
4.20. Су труба арқылы ағады. Трубаның көлденең қимасынан 1 сек уақыт ішінде 200 см3 су ағып өтеді. Тәжірибе жүргізген уақыттағы судың динамикалық тұтқырлығы 0,001 н ∙ сек,/м2-ге тең. Трубаның диаметрінің қандай шекті мәнінде, судың қозғалысы ламинарлық болып қалады?
Не нашли, что искали? Воспользуйтесь поиском: