
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Гармониялық тербелмелі қозғалыс және толқындар
Гармониялық тербелмелі қозғалыстың теңдеуінің түрі мынадай болады
х = A sin (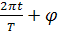 ) = A sin (2
) = A sin (2  ) = Аsin (
) = Аsin (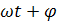 ),
),
мұндағы х — нүктенің тепе-теңдік қалыптан ығысуы, бұл әр түрлі уақыт кезеңінде түрліше болады, А — амплитуда, T-период, 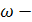 бастапқы фаза, v=
бастапқы фаза, v=  -тербеліс жиілігі,
-тербеліс жиілігі, 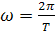 -бұрыштық жиілік
-бұрыштық жиілік
Тербеліс жасайтын нүктенің жылдамдығы мынаған тең:
v= 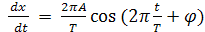
ал үдеуі
a =  sin (
sin (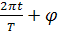 )
)
Массасы m нүктенің әсерінен гармоииялық тербеліс жасайтын күш мынаған тең:
F = ma = -  sin (
sin (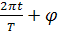 )= -
)= - 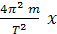 = - kx,
= - kx,
| — -=- |
мұндағы к= 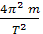 , осыдан T=2
, осыдан T=2 
Осындағы T – Ғ = - kx күштің әсерінен тербеліс жасайтын нүктенің тербеліс периоды, ал k — деформация коэффициенті, ол сан жағынан бірге тең ығысу туғызатын күшке тең болады.
Тербелген нүктенің кинетикалық энергиясы
Wk 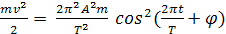
ал потенциалық энергиясы
Wn 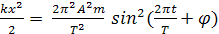
Толық энергия
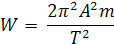
Гармониялық тербелмелі қозғалыстардың мысалы ретінде маятниктің кішкене тербелісін алуға болады. Математикалық маятниктің тербелісінің периоды.
Т  ,
,
мұндағы l — маятниктің ұзындығы, ал g — ауырлық күшінің үдеуі.
Бір жаққа бағытталған периодтары бірдей екі гармониялық тербелістерді қосқанда периоды сол қосылатып тербелістердің периодындай гармониялық тербеліс аламыз, оның амплитудасы мынадай болады:
A= 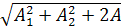 1A2
1A2 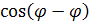 .
.
ал оның бастапқы фазасы мына теңдеу арқылы табылады:
tg  =
= 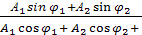
мұндағы A1 мен A2 — қосылған тербелістердің амплитудалары, ал 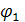 мен
мен 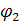 — олардың бастапқы фазалары.
— олардың бастапқы фазалары.
Периодтары бірдей өз араперпендикуляр екі тербелістерді қосқанда, одан шыққан қорытқы қозғалыс траекториясының теңдеуі мына түрде болады:
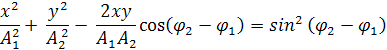
Массасы материялық нүктеге Ғ=—кх серпімді күштен басқа тағы да Ғ үйк = — 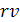 үйкеліс күші әсер етеді десек, онда мұндағы r — үйкеліс коэффициентін, ал v — тербелетін нүктенің жылдамдығын керсетеді, ол уақытта нүктенің тербелісі өшетін тербеліс болады.
үйкеліс күші әсер етеді десек, онда мұндағы r — үйкеліс коэффициентін, ал v — тербелетін нүктенің жылдамдығын керсетеді, ол уақытта нүктенің тербелісі өшетін тербеліс болады.
Өшетін тербелмелі қозғалыстың теңдеуі мына түрде:
х=Ае -81sin (  +
+  ),
),
мұндағы 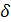 — өшу коэффициенті. Бұл жағдайда
— өшу коэффициенті. Бұл жағдайда 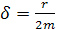 және
және 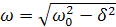 , мұндағы
, мұндағы 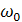 — меншікті тербелістің бұрыштық жиілігі. Шама k =
— меншікті тербелістің бұрыштық жиілігі. Шама k = 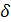 Т тербеліс өшуінің логарифмдік декременті Деп аталады. Тербелісі
Т тербеліс өшуінің логарифмдік декременті Деп аталады. Тербелісі
x1= Ае -81sin 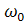 t
t
теңдеумен берілген массасы т материялық нүктеге периодты сыртқы күш Ғ = Ғо sin 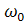 t әсер етеді десек, онда нүктенің тербелісі мәжбүр тербеліс болады да, оның теңдеуінің түрі мынадай болады:
t әсер етеді десек, онда нүктенің тербелісі мәжбүр тербеліс болады да, оның теңдеуінің түрі мынадай болады:
x2= A sin (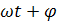 )
)
мұндағы
A = 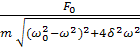
және
tg 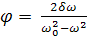
Мәжбүр тербелістің жиілігі 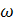 меншікті тербелістің жиілігімен
меншікті тербелістің жиілігімен 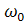 және тербелістің өшу коэффициентімен
және тербелістің өшу коэффициентімен 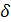 мынадай қатынаспен:
мынадай қатынаспен:
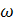 =
= 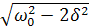
байланысты болғанда резонанс пайда болады.
Өшпейтін тербеліс сәуле деп аталатын кейбір бағыты-ның бойымен с жылдамдықпен тараған уақыттағы, осы сәуленің үстінде тербеліс көзінен l қашықтықта жатқан кез келген нүктенің ығысуы мынадай теңдеумен көрсетіледi:
X = A sin ( )
)
мұндағы А — тербелетін нүктелердің амплитудасы, λ— толқынның ұзындығы. Сонымен бірге λ= сТ. Сәуленің устінде тербеліс көзінен l1 және l2 қашықтықтарда жатқан екі нүктенің фазалар айырмасы мынадай:
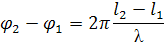
Толкындардың интерференциясы кезіндегі амплитуданың максимумы төмендегі шарт орындалғанда болады
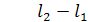 =
= 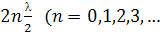 )
)
мұңдағы 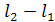 — сәулелер жолының айырмасы.
— сәулелер жолының айырмасы.
Амплитуданың минимумы мынадай шарт орындал-ғанда болады:
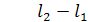 =(2n+1)
=(2n+1) 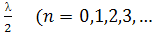 )
)
12.1. 1 мин уақыт ішінде 150 тербедіс жасайтын және тербелістің бастапқы фазасы 45°, амплитудасы 5 см гармониялық тербелмелі қозғалыстың теңдеуін жазу керек.Осы қозғалыстың графигін құру керек.
12.2. Бастапқы фазасы нольге тең, периоды 4 сек, ал амплитудасы 0,1 м гармониялық тербелмелі қозғалыстың теңдеуін жазу керек.
12.3. Гармониялық тербелістің амшштудасы 50 мм, оның периоды 4 сек, ал бастапқы фазасы 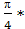 1) Осы тербелістің теңдеуін жазу керек. 2) t = 0 және t =1,5 сек болғанда тербелетін нүктенің тепе-теңдік қалыптан қаншалық ығысатындығын табу керек. 3) Осы қозғалыстың графигін құру керек.
1) Осы тербелістің теңдеуін жазу керек. 2) t = 0 және t =1,5 сек болғанда тербелетін нүктенің тепе-теңдік қалыптан қаншалық ығысатындығын табу керек. 3) Осы қозғалыстың графигін құру керек.
12.4. Тербелістің бастапқы фазалары: 1)0, 2) 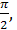 3)
3) 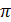 , 4)
, 4) 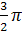 , 5)2
, 5)2 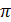 -ге тең болады деп алып, гармониялық тербелмелі қозғалыстың теңдеуін жазу керек. Тербелістің амплитудасы 5 см, ал тербеліс периоды 8 сек. Осы барлық жағдайдағы тербелістің графигін құру керек.
-ге тең болады деп алып, гармониялық тербелмелі қозғалыстың теңдеуін жазу керек. Тербелістің амплитудасы 5 см, ал тербеліс периоды 8 сек. Осы барлық жағдайдағы тербелістің графигін құру керек.
12.5. Амплитудалары (А1=А2 = 2 см) және периодтары (Т1 = Т2 = 8 сек) бірдей, ал фазаларының айырмасы: 1) 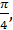 2)
2)  , 3)
, 3) 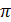 , 4) 2
, 4) 2 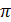 болатын екі гармониялық тербелістерді бір графикке құру керек.
болатын екі гармониялық тербелістерді бір графикке құру керек.
12.6. Гармониялық тербеліс жасайтын нүкте тепе-теңдік қалыптан қозғалыс басынан қанша уақыт өткеннен кейін амплитуданың жартысына ығысатын болады. Тербеліс периоды 24 сек-қа, бастапқы фаза нольге тең.
12.7. Гармониялық тербелістің бастапқы фазасы нольге тең. Периодтың қандай үлесінен кейін нүктенің жыл-дамдығы оның максимал жылдамдығының жартысына тең болады?
12.8. х=7sin 0,5 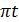 теңдеу бойынша тербелмелі қозғалыс жасайтын нүкте, тепе-теңдік қалыптан максимал ығысуға дейінгі жолды қозғалыс басынан қанша уақыт өткеннен кейін жүреді?
теңдеу бойынша тербелмелі қозғалыс жасайтын нүкте, тепе-теңдік қалыптан максимал ығысуға дейінгі жолды қозғалыс басынан қанша уақыт өткеннен кейін жүреді?
12.9. Гармониялық тербелістің амплитудасы 5 см, ал периоды 4 сек. Тербелетін нүктенің максимал жылдам-дығы мен оның максимал үдеуін табу керек.
12.10. Нүктенің қозғалысы х = 2 sin ( 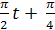 )см теңдеуі түрінде берілген. Мыналарды: 1) тербелістің перибдын,.2) нүктенің максимал жылдамдығын, 3) оның максимал үдеуін табу керек.
)см теңдеуі түрінде берілген. Мыналарды: 1) тербелістің перибдын,.2) нүктенің максимал жылдамдығын, 3) оның максимал үдеуін табу керек.
12.11. Нүктенің қозғалысы x=sin 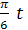 теңдеу түрінде берілген. Нүкте өзінің максимал жылдамдығы мен максимал үдеуіне қандай уақыт моменттерінде жететіндігің табу кереқ.
теңдеу түрінде берілген. Нүкте өзінің максимал жылдамдығы мен максимал үдеуіне қандай уақыт моменттерінде жететіндігің табу кереқ.
12.12. Нүкте гармониялық тербеліс жасайды. Тербеліс периоды 2 сек, амплитудасы 50 мм, ал бастапқы фазасы нольге тең. Нүктенің тепе-теңдік қалыптан алынған ығысуы 25 мм-ге тең болған кездегі жылдамдығын табу керек.
12.13. Нүктенің максимал үдеуі 49,3 см/сек2, тербеліс периоды 2 сек болғандағы нүктенің алғашқы тепе-теңдік қалпынан алынған ығысуы 25 мм гармониялық тербелмелі қозғалыстың теңдеуін жазу керек.
12.14. Гармониялық тербелістің бастапқы фазасы нольге тең. Нүктенің тепе-теңдік қалыптан 2,4 см-ге тең ығысуы кезінде нүктенің жылдамдығы 3 см/сек, ал 2,8 см-ге тең ығысуы кезінде жылдамдығы 2 см/сек. Осы тербелістің амплитудасы мен периодын табу керек.
12.15. Массасы m=1,6-10-2 кг материялық нүктенің тербелісі теңдеуінің түрі мынадай x = 0,1sin (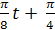 )м. Нүктеге әсер ететін Ғ күштің t уақытқа (бір периодтың шегінде) тәуелділігінің графигін құру керек. Күштің максимал мәнін табу керек.
)м. Нүктеге әсер ететін Ғ күштің t уақытқа (бір периодтың шегінде) тәуелділігінің графигін құру керек. Күштің максимал мәнін табу керек.
12.16. Массасы 10 г материалдық нүкте х = 5 sin ( 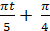 ) см бойынша тербеледі. Нүктеге әсер ететін күш пен тербелетін нүктенің толық энергиясын табу керек.
) см бойынша тербеледі. Нүктеге әсер ететін күш пен тербелетін нүктенің толық энергиясын табу керек.
12.17. Массасы 16 г материалык нүктенің тербеліс теңдеуі мынадай түрде: х= 2 sin (  см берілген. Нүктенің кинетикалық, потенциалық және толық энергияларының уақытқа (бір периодтың шегіндегі) тәуелділігінің графигін құру керек.
см берілген. Нүктенің кинетикалық, потенциалық және толық энергияларының уақытқа (бір периодтың шегіндегі) тәуелділігінің графигін құру керек.
12.18. Мынадай уақыт моменттері үшін: 1) t = 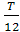 сек, 2) t =
сек, 2) t = 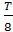 сек, 3) t =
сек, 3) t = 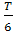 сек гармониялық тербедіе жасайтын нүктенің кинетикалық энергиясынық оның потенциал энергиясына қатынасы неге тең болады? Тербелістің бастапқы фазасы нольге тең.
сек гармониялық тербедіе жасайтын нүктенің кинетикалық энергиясынық оның потенциал энергиясына қатынасы неге тең болады? Тербелістің бастапқы фазасы нольге тең.
12,19. Нүктенің тепе-теңдік қалпынан ығысуы мына моменттер үшін: 1) х=  2) х=
2) х=  3) х=А болғанда гармониялық тербеліс жасайтын нүктенің кинетикалык энергиясының оның потенциал энергиясына қатынасы неге тең болады? Мұндағы А — тербеліс амплитудасы.
3) х=А болғанда гармониялық тербеліс жасайтын нүктенің кинетикалык энергиясының оның потенциал энергиясына қатынасы неге тең болады? Мұндағы А — тербеліс амплитудасы.
12.20. Гармониялық тербелмелі қозғалыс жасайтын дененің толық энергиясы 3- 10-5 дж-ға тең, ал денеге әсер ететін максимал күш 1,5- 10-3 н-ға тең. Тербёлістің периодын 2 сек-қа, ал бастапқы фазасын 60°-қа тең деп,осы денёнің қозғалыс теңдеуін жазу керек.
12.21. Материялық нүктеиің гармониялық тербелісі-нің амплитудасы A = 2 см, ал тербелістің толық энергиясы W = 3 • 10-7 дж. Тербелістегі нүктенің тепе-теңдік қалпынан есентегендегі қандай ығысуында оған әсер ететін күш Ғ = 2,25 • 10-5 н болады?
12.22. Ұзындығы 2 м жіпке ілінген шарикті 4° бұрышқа бұрып, оның тербелісін бақылайды. Тербелісті гармониялық өшпейтін деп есептеп, шариктің тепе-теңдік қалыптан өткендегі жылдамдығын табу керек. Шариктің тёпе-теңдік қалыптан өткендегі жылдамдығын механикадағы теңдеу арқылы тауып есептің шешуін тексеріңіздер.
12.23. Пружинаға 10 кГ жүк ілінген. 1 кГ күштің әсерінен пружина 1,5 сл-ге созылатындығын біле отырып, осы жүктің вертикаль тербелісінің периодын анықтау керек.
12.24. Пружинаға жүк ілінген. Жүктің тербелісінің максимал кинетикалық энергиясы 1 дж-ға тең болады деп алып, пружина деформациясының коэффициентін табу керек. Тербелістің амплитудасы 5 сж-ге тең.
12.25. Жүктер бірдей екі пружинаға ілінген. Егер пру-жиналарды бір-бірімен тізбектеп жалғастырудан параллель жалғастыруға ауыстырсақ, онда оларға ілінген жүктің вертикаль тербелісінің периоды қалай өзгереді?
12.26. Пружинаға іліп қойған мыс шарик вертикаль тербеліс жасайды. Егер осы пружинаға радиусы мыс шаригінің радиусына тең болатын алюминий шаригін ілсек, онда осы шариктің вертикаль тербелісінің периоды қалай езгереді?
12.27. Үстіне гир салынған таразының табақшалары пружинаға ілінген, Осы уақытта вертикаль тербелістің периоды 0,5 сек-қа тең болды. Таразыньщ табақшаларына қосымша гир салынғаннан кейінгі оның вертикаль тербелісінің периоды 0,6 сек-қа тең болды. Осы қосымша гирдің әсерінен пружинаның қаншаға ұзарғанын табу керек?
12.28. Ұзындығы 40 см, ал радиусы 1 мм резеңке жіпке салмағы 0,5 кГ гир ілінген. Осы резеңкенің Юнга модулі 0,3 кГ/мм2-ге тең деп алып, гирдің вертикаль тербелісінің периодын табу керек.
Н ұ с қ а у. Резеңкенің к деформация коэффициентінің резеңкенің Е Юнга модулімен мынадай қатынас арқылы байланыста болатындығын ескеру керек к = 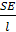 , мұндағы S — резеңкенің көлденең қимасының ауданы, ал l — оның ұзындығы.
, мұндағы S — резеңкенің көлденең қимасының ауданы, ал l — оның ұзындығы.
12.29. Сұйықтың ішінде жүзіп жүрген ареометрдің салмағы Р = 0,2 кГ. Егер осы ареометрді сұйықтың ішіне шамалы батырып, содан кейін босатып жіберсек, онда ол T=3,4 сек периодпен тербеліс жасай бастайтын болады. Тербелісті өшпейтін деп есептеп, осы тәжірибедегі мәліметтер бойынша ареометр жүзіп жүрген сұйықтық тығыздығын табу керек. Ареометрдің цилиндр тәрізді вертикаль түтігінің диаметрі d = 1 см-ге тең.
12.30. Бір жаққа қарай бағытталған периодтары бірдей 8 сек-қа тең және амплитудалары да бірдей 0,02 м екі гармониялық тербелмелі қозғалысты қосқанда пайда болатын қозғалыстың теңдеуін жазу керек. Осы тербелістердің арасындағы фаза айырмасы  ке тең. Тербелістің біреуінің бастапқы фазасы нольге тең.
ке тең. Тербелістің біреуінің бастапқы фазасы нольге тең.
12.31. x1= 0,02 sin (5 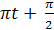 ) м және х2 = 0,03 sin Х Х (5
) м және х2 = 0,03 sin Х Х (5 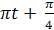 ) м теңдеулермен берiлген, бір жаққа қарай бағытталған тербелістерді қосудан пайда болған гармониялық тербелістің амплитудасын және бастапқы фазасьш табу керек.
) м теңдеулермен берiлген, бір жаққа қарай бағытталған тербелістерді қосудан пайда болған гармониялық тербелістің амплитудасын және бастапқы фазасьш табу керек.
12.32. Бір бағыттағы амплитудалары мен периодтары бірдей екі гармониялық тербелісті қосудың нәтижесінде периоды мен амплитудасы сондай қорытқы тербеліс шығады. Қосылатын тербелістердің фаза айырмасын табу керек.
12.33. 1)Теңдеулері x1 = 4 sin 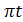 см және х2=3 (
см және х2=3 (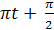 см түрде берілген, бір жаққа қарай бағытталған, екі гармониялық тербелістерді қосудың нәтижесінде пайда болған гармониялық тербелістің амплитудасын және бастапқы фазасын табу керек
см түрде берілген, бір жаққа қарай бағытталған, екі гармониялық тербелістерді қосудың нәтижесінде пайда болған гармониялық тербелістің амплитудасын және бастапқы фазасын табу керек
2)Қорытқы тербелістің теңдеуін жазу керек.
3) Амплитудалар ды қосудың векторлық диаграммасын беру керек
12.34. 61-суретте күрделі тербелістің спектрі берілген. 1) Осы суреттегі берілгендерді пайдаланып, күрделі тербелісті құрап тұрған тербелістердің теңдеуін жазу керек. 2) Осы тербелістің графигін кұру керек. (Осы тербелістердің арасындағы t = 0 моменттегі фаза айырмасын нольге тең-деп аламыз). 3) Kүрделі қорытқы тербелістің графигін құру керек.
12.35. Екі гармониялық тербеліс Х1 = 3 sin 4 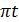 см жәе х2 = 6 sin 10
см жәе х2 = 6 sin 10 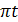 см берілген. Осы тербелістердің графигін құру керек. Оларды график түрінде қосып, алынған қорытқы тербелістің графигін құру керек. Тауып алынған күрделі тербелістің спектрін сызу керек.
см берілген. Осы тербелістердің графигін құру керек. Оларды график түрінде қосып, алынған қорытқы тербелістің графигін құру керек. Тауып алынған күрделі тербелістің спектрін сызу керек.
12.36. Тербеліс мынадай теңдеу арқылы берілген (1)
х=А sin 2 
мұндағы А — уақытқа байланысты А =Aо(1 +соs 2 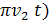 заңы бойынша өзгереді. Осындағы A0 = соnst болады. Тербеліс (1) қандай гармониялық тербелістерден тұратынын табу кереқ. A0 = 4 см, v1= 2 сеk-1, v2=1 сек-1 жағдайлары үшін құраушы және қорытқы тербелістердің графигін құру керек. Күрделі тербелістіқ спектрін сызу керек.
заңы бойынша өзгереді. Осындағы A0 = соnst болады. Тербеліс (1) қандай гармониялық тербелістерден тұратынын табу кереқ. A0 = 4 см, v1= 2 сеk-1, v2=1 сек-1 жағдайлары үшін құраушы және қорытқы тербелістердің графигін құру керек. Күрделі тербелістіқ спектрін сызу керек.
12.37. Жиіліктері бірдей v1 = v2 = 5 гц және бастапқы фазалары бірдей 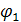 =
= 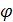 2 = 60° екі өз ара-перпендикуляр тербелістерді қосудың нәтижесінде пайда болған корыт-қы тербелістің теңдеуін жазу керек. Тербелістердің біреуінің амплитудасы A1= 0,1 м, ал екіншісінің амплитудасы A2 = 0,05 м-ге тең.
2 = 60° екі өз ара-перпендикуляр тербелістерді қосудың нәтижесінде пайда болған корыт-қы тербелістің теңдеуін жазу керек. Тербелістердің біреуінің амплитудасы A1= 0,1 м, ал екіншісінің амплитудасы A2 = 0,05 м-ге тең.
12.38. Нүкте периодтары да және бастапқы фазалары да бірдей екі тербелістерде қатысады. Тербелістің амплитудалары A1= 3 см және A2 = 4 см. 1) тербелістерді бірдей бағытта, 2) өз ара-перпендикуляр бағыттарда өтеді деп алып, қорытқы тербелістің амплитудасын табу керек.
12.39. Нүкте бір мезгілде өз ара-перпендикуляр екі тербелістерге х — 2 sin  м және y = 2 соs
м және y = 2 соs  м қатысады. Осы нүктенің қозғалысының траекторшісын табу керек.
м қатысады. Осы нүктенің қозғалысының траекторшісын табу керек.
12.40. Нүкте бір мезгілде өз ара-перпендикуляр екі тербелістерге х=соs 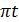 жэне у = соs
жэне у = соs  қатысады. Осы нүктенің қорытқы қозғалысының траекториясын табу керек.
қатысады. Осы нүктенің қорытқы қозғалысының траекториясын табу керек.
12.41. Нүкте бір мезгілде ез ара-перпендикуляр екі тербелістерге х=sin 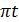 және у = 2 sin * (
және у = 2 sin * ( 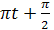 ) қатысады. Нүктенің қозғалысының траекториясын табу керек және оны масштабын көрсете отырып сызып шығару керек,
) қатысады. Нүктенің қозғалысының траекториясын табу керек және оны масштабын көрсете отырып сызып шығару керек,
12.42. Нүкте бір мезгілде ез ара-перпендикуляр екі тербелістерге х = sin 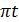 және y=4 sin(
және y=4 sin( ) катысады. Нүктенің қозғалысының траекториясын табу керек және оның масштабын керсете отырып сызып шығару керек.
) катысады. Нүктенің қозғалысының траекториясын табу керек және оның масштабын керсете отырып сызып шығару керек.
12.43. Өшетін тербелістің периоды 4 сек, өшудің логарифмдік декременті 1,6, ал бастапқы фазасы нольге тең. Уақыт t =  болғандағы нүктенің ығысуы 4,5 см-ге тең. Осы тербелмелі қозғалыстың екі периодтың шегіндегі графигін құру керек.
болғандағы нүктенің ығысуы 4,5 см-ге тең. Осы тербелмелі қозғалыстың екі периодтың шегіндегі графигін құру керек.
12.44. Теңдеуі x=е-0.1t sin  м түрде берілген өшетін тербелістің графигін құру керек.
м түрде берілген өшетін тербелістің графигін құру керек.
12.45. Өшетін тербелістің теңдеуі x=5е-0.25t sin 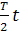 м түрде берілген. Уақыт моменттері: 0, Т, 2Т, 3Т және 4Т болғанда тербеліп тұрған нүктеніқ жылдамдығын табу керек.
м түрде берілген. Уақыт моменттері: 0, Т, 2Т, 3Т және 4Т болғанда тербеліп тұрған нүктеніқ жылдамдығын табу керек.
12.46. Математикалық маятниктің тербеліс өшуінің логарифмдік декременті 0,2-ге тең. Маятниктің бір толық тербелісінде тербеліс амплитудасыньщ неше есеге кемитіндігін табу керек?
12.47. Егер 1 мин ішінде тербеліс. амплитудасы екі есе кеміді десек, онда математикалық маятниктің өшуі-нің логарифмдік декременті неге тең болады? Маятниктің үзындығы 1 м-те тең.
12.48. Ұзындығы 24,7 см математикалық маятник өше-тін тербеліс жасайды. Маятниктің тербеліс энергиясы қанша уақыттан кейін 9,4 есе кемитін болады? Есепті шудің логарифмдік декрементінің 1) х=0,01 және 2) х= 1 мәндері үшін шешу керек.
12.49. Өшетін тербеліс жасайтын математикалық маятниктің өшуінің логарифмдік декременті 0,2-ге тең. Маятниктің бір толық тербелісінің ең шеткі қалпындағы оның толық үдеуі неше есе кемиді?
12.50. Математикалық маятниктің өшетін тербелісі-нің амплитудасы 1 мин ішінде екі есе кемиді. Оның 3 мин ішінде неше есе кемитіндігін табу керек?
12.51. Тепе-теңдік қалыптан шығарылған үзындығы 0,5 м математикалық маятник бірінші тербелгенінде 5 слг-ге, ал екінші тербелгенінде (сол алғашқы жаққа қарай) 4 сж-ге бұрылды. Релаксация уақытын, яғни тербеліс амплитудасының ішінде е есе кемитін уақытты табу керек, мұндағы е — натураль логарифмнің негізі.
12.52. Вертикаль қалыпта тұрған пружинаға жүк ілінген. Осыдан пружина 9,8 сж-ге ұзарады. Жүктің оны төмен қарай созып, содан кейін қайтадан орнына келуі жүкті тербеліс жасауға мәжбүр етеді. Тербеліс 10 сек ішінде тоқталу үшін -(олардың амилитудасы бастапқы шамасынан 1 процентке дейін темендеді деген ұйғарымды шартты түрде аламыз), 2) жүк тепе-теңдік қалпына периодты түрде келуі үшін және өшудің логарифмдік декременті 6-ға тең болу үшін ешу коэффициенті 6 неге тең болу керек?
12.53. Массасы т=10 г дене максимал мәні 7 см-тс тең амплитудамен өшетін тербеліс жасайды, бастапқы фазасы нольге тең және өшу коэффициенті 1,6 сек_1-ге тең. Осы денеге периодты сыртқы қүш әсер ете бастаған-нан еріксіз тербеліс орнайды. Еріксіз тербелістің теңдеуі мына турде болады: х=5 sin (10 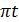 — 0,75
— 0,75 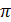 ) см болады. Мыналарды: 1) өздік тербеліс теңдеуін (сан коэффииенттерімен), 2) периодты сыртқы күшгің теңдеуін (сан коэффициенттерімен) табу керек.
) см болады. Мыналарды: 1) өздік тербеліс теңдеуін (сан коэффииенттерімен), 2) периодты сыртқы күшгің теңдеуін (сан коэффициенттерімен) табу керек.
12.54. Вертикаль пружинаға ілінген салмағы 0,2 кГ гир өшу коэффициенті 0,75 сек-1-ге теқ ешетін тербеліс жасайды. Пружинаның деформаций коэффициенті 0,5 кГ/см. Гирдің мәжбүр тербелісінің А амплитудасының периодты сыртқы күштің 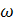 жиілігіне тәуелді болатын-дығын сызып керсету керек. Сыртқы күштің ең үлкен мәні 0,98 я-ге тең деп аламыз. Графикті құруда мына жиіліктер үшін
жиілігіне тәуелді болатын-дығын сызып керсету керек. Сыртқы күштің ең үлкен мәні 0,98 я-ге тең деп аламыз. Графикті құруда мына жиіліктер үшін 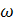 = 0,
= 0, 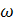 = 0,5
= 0,5 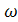 о,
о, 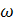 = 0,75
= 0,75 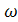 о,
о, 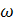 =
= 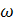 о,
о, 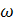 =1,5
=1,5 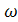 о және
о және 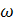 = 2
= 2 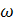 о А амплитуданың мәнін табу керек, мұндағы
о А амплитуданың мәнін табу керек, мұндағы 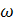 о — іліп қойған гирдің ездік тербеліс;нің жиілігі.
о — іліп қойған гирдің ездік тербеліс;нің жиілігі.
12.55. Қара жолмен жүріп өткен т^актор, өзінің соңында бір-бірінен 30 см қашықтықта қатар-қатар жатқан ойыс түрінде із қалдырды. Осы жолмен 1 кГ күштіц әсерінен әрқайсысы 2 cм-ге майысатын Бірдей екі рессоры бар арбаны бала сүйретіп өтеді. Осы арбаны бала жолмен сүйретіп алып жүргенде арба дөцгелегінің ойыстарға түсіп соққылануынан ол резонансқа келті, өте қатты шай-қала бастаған болса, онда арба қандагі жылдамдықпен сүйретілген? Бала арбасының салмағы 10 кГ.
12.56. Периоды 10~14 сек-қа тең терселіс толқынының ұзындығын табу керек. Тербелістің таралу жылдамдығы 3 • 108 м/сек-қа тең.
12.57. Жиілігі v = 500 гц және ампльтудасы A = 0,25 м дыбыс тербелісі ауада тарайды. Толқь;ғның ұзындығы һ=70 см. Мыналарды: 1) тербелістің таралу жылдамдығын, 2) ауа бөлшегінің максимал жылдамдығын табу керек.
12.58. Өшпейтін тербелістің теңдеуі x=10 sin 0,5 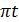 см түрде берілген. 1) Тербелістің таралу жылдамдығын 300 м/сек деп алып, толқынның теңдеуің табу керек. 2) Тербеліс кезінен 600 м қашықтықта тұрған нүкте үшін берілген тербелістің теңдеуін жазьш және график арқылы керсету керек. 3) Тербеліс басталғаннан 4-сек өткеннен кейінгі моменттегі толқын нүктесі үшін тербеліс теңдеуін жазып және график арқылы көрсету керек.
см түрде берілген. 1) Тербелістің таралу жылдамдығын 300 м/сек деп алып, толқынның теңдеуің табу керек. 2) Тербеліс кезінен 600 м қашықтықта тұрған нүкте үшін берілген тербелістің теңдеуін жазьш және график арқылы керсету керек. 3) Тербеліс басталғаннан 4-сек өткеннен кейінгі моменттегі толқын нүктесі үшін тербеліс теңдеуін жазып және график арқылы көрсету керек.
12.59. Өшпейтін тербелістің теңдеуі х = А sin 600 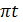 см түрде берілген. Тербеліс басынан 0,01 сек өткеннен кейін тербеліс көзінен 75 см қашықтықта тұрған нүктенің тепе-теңдік қалыптан ығысуын табу керек. Тербелістіқ таралу жылдамдығы 300 м/сек.
см түрде берілген. Тербеліс басынан 0,01 сек өткеннен кейін тербеліс көзінен 75 см қашықтықта тұрған нүктенің тепе-теңдік қалыптан ығысуын табу керек. Тербелістіқ таралу жылдамдығы 300 м/сек.
12.60. Өшпейтін тербелістің теңдеуі х=sin 2,5 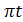 см түрде берілген. Тербеліс басынан 0,01 сек өткеннен кейін момент үшін тербеліс көзінен 20 м қашықтықта тұрған нүктенің үдеуі мен жылдамдығын және тепе-теңқдік қалыптан ығысуын табу керек. Тербелістің таралу жылдамдығы 100 м/сек.
см түрде берілген. Тербеліс басынан 0,01 сек өткеннен кейін момент үшін тербеліс көзінен 20 м қашықтықта тұрған нүктенің үдеуі мен жылдамдығын және тепе-теңқдік қалыптан ығысуын табу керек. Тербелістің таралу жылдамдығы 100 м/сек.
12.61. Тербеліс көзінен сәйкес 10 және 16 м қашықтықта тұрған екі нүктекің тербеліетерінің фазалар айырмасы қандай болады? Тербеліс периодтары 0,04 сек, ал тербелістің таралу жылдамдығы 300 м/сек.
12.62. Сәуленің үстінде бір-бірінен 2 м қашықтықта жатқаи екі нүктенің тербелісінің, фазалар айырмасын табу керек. Толқынньщ ұзындығы 1 м-ге тең.
12.63. t=  моменті үшін, тербеліс кезінен l=
моменті үшін, тербеліс кезінен l= 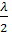 қашықтықта жатқан нүктенің тепе-теңдік қалыптан алынғап ығысуын табy керек. Тербелістін амплитудасы A = 0,05м.
қашықтықта жатқан нүктенің тепе-теңдік қалыптан алынғап ығысуын табy керек. Тербелістін амплитудасы A = 0,05м.
12.64. Тербеліс көзінен 4 см қашықтықта жатқан нүктенің t =  моменттегі тепе-тендік қалыптан ығысуы амплитуданың жартысына тең. Жүгірме толқынның ұзындығын табу керек.
моменттегі тепе-тендік қалыптан ығысуы амплитуданың жартысына тең. Жүгірме толқынның ұзындығын табу керек.
12.65. Мына: 1) толқынның шағылысуы тығыздығы кішкене ортада өтеді және 2) толқынның шағылысуы тығыздығы үлкен ортада өтеді деген екі жағдай үшін тұрғын толқынның графигін сызып және оның түйіні мен шоқтығының пайда болатын орнын табу керек. Жүгірме толқынның ұзындығы 12 сл-ге тең. Тұрғын толқынның бірінші және төртінші шоқтықтарының араларының қашықтығы 12 с
Акустика
Акустикалық тербелістің кейбір ортада таралуының жылдамдығы мынадай формуламен анықталады:
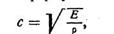
мұндағы Е — ортаның Юнга модулі, ал ρ — ортаның тығыздығы.
Газдардың ішінде тербелістің таралуының жылдамдығы мынадай:

мұндағы ц — газдың бір киломолінің массасы, Т — газдың абсолюттік температурасы, R — газ тұрақтысы,  болады (Ср —қысым тұрақты болғандағы газдың жылу сыйымдылығы, ал Сv — көлем тұрақты болғандағы газдың жылу сыйымдылығы).
болады (Ср —қысым тұрақты болғандағы газдың жылу сыйымдылығы, ал Сv — көлем тұрақты болғандағы газдың жылу сыйымдылығы).
Децибелмен берілген L1 дыбыс қысымы деңгейінің Δр, дыбыс қысымының амплитудасымен байланысы мы-надай қатынас арқылы беріледі:

мұндағы Δро — дыбыс қаттылығының нольдік деңгейіндегі дыбыс кысымының амплитудасы. Фонмен берілген дыбыс қаттылығының деңгейі L2 дыбыс интенсивтігімен мынадай қатынас арқылы байланысады:

мұндағы І о — дыбыс қаттылығынық нольдік деңгейі. Шартты түрде ол былай алынады:
I 0=10-12 вт/м2 және Δро=2 • 10-5 н/м2. Допплердің принципі бойынша бақылаушымен қабылданатын дыбыстың жиілігі мынадай формуламен анық-галады:
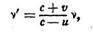
мұндағы v —дыбыс көзінің шығаратын дыбыстың жиілігі, и — дыбыс көзінің қозғалыс жылдамдығы, ν — бақылаушының қозғалыс жылдамдығы және с — дыбыстың таралу жылдамдығы. Егер бақылаушы дыбыс көзіне қараған бағытпен қозғалады десек, онда жылдамдық v>0 болады; ал дыбыс көзі бақылаушыға қарай қозғалса, онда u<0 болады.
Сым ішектің негізгі тонының жиілігі, мынадай формуламен анықталады:

мұндағы l — сым ішектің ұзындығы, F-оның керілу күші, 5 — оның көлденең қимасының ауданы, ал ρ — орта затының (материалының) тығыздығы.
13.1. Жиілігі 435 гц негізгі тон ля-нің толқын ұзындығын табу керек. Дыбыстың жылдамдығын 340 м/сек-қа тең деп аламыз.
13.2. Адамның құлағы шамамен алғанда жиілігі 20-дан 20 000 гц-ке дейінгі дыбысты қабылдай алады. Дыбыс тербелісінің естілу интервалы қандай толқындар ұзындығының арасында жататындығын табу керек? Ауа-дағы дыбыстың жылдамдығын 340 м/сек-ке тең деп аламыз.
13.3. Болат ішіндегі дыбыстың таралу жылдамдығын табу керек.
13.4. Мыс ішіндегі дыбыстың таралу жылдамдығын табу керек.
13.5. Керосиннің ішіндегі дыбыстық таралу жылдамдығы 1330 м/сек. Керосиннің сығылу коэффициентін табу керек.
13.6. Теңіздің тереңдігін эхолоттың көмегімен өлшейді. Дыбыстың пайда болып және оны қабылдағанға дейінгі уақыт аралығы 2,5 сек-қа теқ болса, онда теқіздің тереңдігі қандай болғаны? Судың сығылу коэффициенті 4,6 • 10-10 м2/н және теңіз суының тығыздығы 1030 кг/м3.
13.7. Мына температуралардағы: 1) -20°С, 2) 0°С, 3) +20°С дыбыстың ауада таралуының жылдамдығын табу керек.
13.8. Жазды күнгі дыбыстың ауада таралуының жыл-дамдығы (температура +27оС) қысты күнгі дыбыстық ауада таралуының жылдамдығынан (температура —33°С) неше есе үлкен болады?
13.9. Тәжірибе жағдайында екі атомды газ молекуласының орташа квадраттық жылдамдығы 461 л/сек-қа тең болғанын біле отырып, осы жағдайдағы дыбыстың таралу жылдамдығын табу керек.
13.10. 760 мм. сын. бағ. қысымда екі атомды газдың тығыздығы 1,29 • 10-3 г/см3-те тең болады деп алып, осы газ арқылы дыбыстың таралу жылдамдығын табу керек.
13.11. Бір киломоль азот молекуласынық ілгерілемелі қозғалысының орташа кинетикалық энергиясы 3,4 • 103 кдж-ға тең екендігін біле отырып, осы шарттағы азот арқылы дыбыстың таралу жылдамдығын табу керек.
13.12. Атмосфераның жоғарғы қабатының температурасын анықтау үшін термометрді пайдалануға болмайды, өйткені газ тығыздығының аздығынан термометр қоршап тұрған ортамен жылулық тепе-теңдікке келе алмайды. Осы мақсатта белгілі бір биіктікте жарылатын гранат бар ракета жіберіледі. 21 км биіктіқте жасалған жарылудан пайда болған дыбыс 19 км биіктікте жасалған жарылудан пайда болған дыбыстан 6,75 сек кейін естілгендігі белгілі деп, жердің бетінен 20 км биіктіктегі температураны табу керек.
13.13. Ауа — шыны шекарасындағы дыбыс толқынының сыну көрсеткіші неге тең болады? Шыны үшін Юнга модулі 6,9 • 1010н/м2-ге тең, шынының тығыздығы 2,6 г/см3, ал ауаның температурасы 20°С.
13.14. Ауа — шыны шекарасындағы дыбыс толқынының толық ішкі шағылысуының шекті бұрышын табу керек. Есепті шығаруға керекті мәліметтерді алдыңғы есептен алып пайдалану керек.
13.15. Екі дыбыстың қаттылық деңгейі жағынан айырмашылықтары 1 фон. Осы дыбыстардың интенсивтігінің қатысын табу керек.
13.16. Екі дыбыстың дыбыс қысымының деңгейі жағынан айырмашылықтары 1 дб. Олардың дыбыс қысымдары амплитудаларының қатынасын табу керек.
13.17. Қаттылығы 70 фон көшедегі шу, қаттылығы 40 фон шу сияқты бөлмеге естіледі. Көшедегі және бөлмедегі дыбыстың интенсивтігінің қатынасын табу керек.
13.18. Дыбыстық интенсивтігі 1000 есе өсті. 1) Осы уақыттағы дыбыстың кысым деңгейі қанша децибелге өсті? 2) Дыбыс қысымының амплитудасы неше есе өсті?
13.19. Дыбыстың интенсивтігі 10-2 в/м2-ге тең. Мыналарды: 1) қаттылық деңгейін, 2) дыбыс қысымының амплитудасын табу керек.
13.20. Егер дыбыстың интенсивтігі: 1) 3000 есе және 2) 30 000 есе өсті десек, онда дыбыс қаттылығының деңгейі қанша фонға өсетін болады?
13.21. Граммофон пластинкасындағы ля (435 гц) тонына арналған дыбыс бороздаларынын, көршілес тістерінің ара қашықтығын мынадай шарттар үшін: 1) пластинкаға жазудың басындағы центрден алғандағы 12 см қ а-шықтық үшін, 2) пластинкаға жазудың аяғындағы 4 см қашықтық үшін табу керек: Пластинканың айналу жылдамдығы 78 айн/мин.
13.22. Мына жиіліктер үшін v = 100 гц және v =2000 гц жасалған граммофон пластинкасындағы дыбыс бороздаларының көршілес тістерінің ара қашықтығын табу керек. Пластинканың центрінен алынған орташа қашықтықты 10 см-ге тең деп есептейміз. Пластинканың айналу жылдамдығы 78 айн/мин.
13.23. Кундт түтігінің ішінде тұрғын толқын жасағанда ауа бағанасында. 6 шоқтықтың пайда болғаны байқалды. Егер болат стержень бағананың: 1) ортасына, 2) ұшынан бекітілген десек, ауа бағанасының ұзындығы қандай болғаны? Стерженьнің ұзындығы 1 м. Болаттағы дыбыстың жылдамдығы 5250 м/сек және ауадағы дыбыстың жылдамдығы 343 -м/ceк-қа тең.
13.24. Кундт түтігінің ішіндегі шыны стерженьді ортасынан бекіткенде ауа бағанасында 5 шоқтылықтың пайда болғаны байқалса, онда стерженьнің ұзындығы неге тең болғаны? Ауа бағанасының ұзындығы 0,25 м. Шыны үшін Юнга модулі 6,9 • 1010 н/м2, ал шыныныц тығыздығы 2,5 г\см3 Ауадағы дыбыстың жылдамдығын 340 м/сек-қа тең деп аламыз.
13.25. Шоқтардың араларын байқауға болатын ең кішкене қашықтық l =4 мм-гe тең болады десек, дыбыстың жылдамдығын анықтауға арналған Кундттың әдісін қандай ең үлкен жиіліктер үшін қолдануға болады? Ауадағы AH6HcfHH жылдамдығын 340 м/сек-қа тең деп аламьіз?
13.26. Бір-біріне қарсы жүріп келе жатқан екі поез-дың жылдамдықтары 72 км/сағ және 54 км/сағ. Бірінші Іірездың ыскырығының.жиілігі 600 гц. Мыналарды: 1) поёздардың кездесуінің алдындағы жәйе 2) поездардың кездесуінен кейінгі екінші поездағы жолаушының еcтитін дыбыс тербелісінің жиілігін табу керeк. Дыбыстың жылдамдығын 340 ж/се/с-қа тең деп аламыз.
13.27. Поезд қозғалмай тұрған бақылаушының жанынан өткен уақытта паровоздың гудогінің тон биіктігі кенет өзгеріп кетеді. Егер поезд 60 км/сағ жылдамдықпен қозғалған болса, онда тонның кенет өзгеруінің шамасы шын жиілігінің қанша процентін беретін болады?
13.28. Теңіздің жағасында тұрған бақылаушы пароход гудогінің дыбысын естиді. Бақылаушы мен пароход тыныштық жағдайда тұрған кезде бақылаушының қабылдаған дыбысы 420 гц жиілікке сәйкес келеді. Пароход-тың бақылаушыға қарай бағытталған қозғалысында қабылданған дыбыстың жиілігі 430 гц-ке тең болды. Пароходтың бақылаушыдан бері қарай бағыттағы қозғалысындағы жиілік 415 г-ке тең. Тәжірибе жағдайындағы дыбыс жылдамдығы 338 м/сек-қа тең деп алып, бірінші және екінші жағдайлардағы пароходтың жылдамдығын анықтау керек.
13.29. Мылтықтың оғы 200 м/сек жылдамдықпен ұшады. Жанынан оқ ұшып өткен, қозғалмай тұрған бақылаушы үшін оқ ысқырығының тон биіктігі неше есе өзгеретінін табу керек. Дыбыстың жылдамдығын 333 м/сек-қа тең деп аламыз.
13.30. Екі поезд бірдей жылдамдықпен бір-біріне қарсы жүріп келе жатыр. Осылардың бірінің, екіншісіне естілетін, ысқырығының тон биіктігі 9/8 есе өзгеру үшін олардың жылдамдығы қандай болу керек? Дыбыстың жылдамдығын 335 л/сек-қа тең деп аламыз.
13.31. Қабырғаға перпендикуляр бағытта v =6,0 м/сек жылдамдықпен үшып келе жатқан жарқанат жиілігі v =4,5 · 1 04гц ультра дыбыс шығарады. Жарқанат қандай екі жиіліктің дыбысын еститін болады? Дыбыстың жыл-дамдығын 340 м/ск-қа тең деп аламыз.
13.32. Радиусы 0,05 cм болат шекті 100 кГ күшпен кергенде жиілігі 320 гц тон шығару үшін оның ұзындығы қаңдай болу керек?
13.33. Ля нотасын (жиілігі 435 гц) шығару үшін ұзындығы 20 см, ал диаметрі (0,2 мм болат шекті қандай күшпен керу керек?
13.34. Болат үшін беріктік шегін біле отырып, ұзындығы 1 м шектің құлақ күйіне келтіруге болатын ең үлкен жиілігін табу керек.
13.35. 15 кГ қүшпен керілген сым шек бір секундта камертонмен бірге 8 соғу береді. Осы сым шекті 16 кГ күшпен кергеннен кейін ол камертонмен унисондағы құлақ күйіне келтіріледі. Камертонның тербеліс санын табу керек.
13.36. Алдыңғы есептегі камертон басқа камертонмен бірге 5 сек ішінде 10 соғу береді. Екінші камертонның тербёліс жиілігін табу керек.
13.37. Ғ =6 · 103 н күшпен керілген сым шектің негізгі тонының жиілігін табу керек. Сым шектің ұзындығы l =0,8 м, ал оның салмағы Р=0,03 кГ.
13.38. Мыналарды: 1) ашық трубаның және 2) жабық трубаның негізгі тондарының жиілігін табу керек.
13.39. Жабық труба, 130,5 гц жиілікке сәйкес келетін, негізгі до тонын шығарады. Егер трубаны ашып қойса, ол қандай негізгі тон шығаратын болады? Трубаның ұзындығы қандай? Ауадағы дыбыстың жылдамдығын 340 м/сек-қа тең деп аламыз.
Не нашли, что искали? Воспользуйтесь поиском: