Действия над числами, выраженными

МЕРАМИ ВРЕМЕНИ

При изучении данной темы у школьников с нарушением интел­лекта возникает много трудностей и ошибок, которые учитель должен предупредить. Первая группа ошибок связана с недоста­точно твердым знанием соотношения мер. Вторая группа ошибок возникает из-за буквального переноса на действия с числами, выраженными мерами времени, действий с числами, полученными от измерения других величин.

Например:

Для предупреждения подобного рода ошибок всегда необходимо:

а) систематически повторять соотношение мер времени и сопо­
ставлять с соотношением единиц метрической системы; подчерки­
вать, что меры времени не метрические;

б) сопоставлять действия с числами, выраженными мерами
времени, и действия с числами, полученными от измерения дру­
гих величин:

в) анализировать числа, над которыми производятся действия,
тщательно соблюдать последовательность при выборе примеров,
учитывая нарастающую степень их трудности.

Сложение и вычитание

Сначала рассматриваются те упражнения на сложение и вычи­тание, в которых сумма минут (секунд) меньше, чем 60, сумма часов меньше, чем 24, сумма месяцев меньше, чем 12.

Выполнение упражнений такого вида можно проводить и устно без записи или с записью в строчку. Они, как правило, включают­ся в устный счет.

После этого рассматриваются более сложные упражнения, в которых сумма минут (секунд) равна или больше 60, сумма часов больше 24, сумма месяцев больше, чем 12, и т. д., и при вычита­нии крупные меры необходимо выразить в мелких.

Рассмотрение таких упражнений целесообразно проводить в такой последовательности:

3 ч 20 мин

Арифметические действия с числами, выраженными в мерах времени и мерах метрической системы, сравниваются, устанавли­ваются их сходство и различие.

Например: «Реши примеры, объясни их решение. В чем сходст­во и в чем различие решения этих примеров?»

3 ч 58 мин. 3 о. 58 к. 7 м 40 см 7 ч 40 мин

Вопросы и задания

1. Каковы дидактические требования изучения единиц измерения време­
ни, развития временных представлений учащихся с интеллектуальным недо­
развитием?

2. Составьте фрагмент одного из уроков по ознакомлению учащихся с
единицами измерения времени: час, минута, год.

3. Сравните решение примеров: 535—248, 5 р. 35 к.—2 р. 48 к.,
5 ч 35 мин—2 ч 48 мин. Какой из этих примеров вызовет наибольшие
трудности у учащихся? Почему?

4. На примерах из учебников математики покажите задания, направлен­
ные на развитие мышления и речи учащихся при развитии временных пред­
ставлений.

Глава 17

МЕТОДИКА ИЗУЧЕНИЯ ОБЫКНОВЕННЫХ ДРОБЕЙ

К моменту изучения долей, а затем и обыкновенных дробей у школьников с нарушением интеллекта имеется уже некоторый жизненно-практический опыт в образовании и наблюдении долей целых предметов или величин.

В играх, в своей практической деятельности они сталкивались с потребностью разделить целый предмет на равные части, напри-292

мер: распилить доску пополам, отрезать половину или четверть ленты, тесьмы, разрезать репу, булку, яблоко на две или четыре равные части, разделить пополам конфету, разделить на две, три, четыре равные части отрезок и т. д.

Однако при изучении дробей учащиеся встречаются со многи­ми новыми свойствами и качествами дробных чисел, значительно отличающими их от натуральных: название, запись, возможность выполнения таких преобразований над дробями, которые изменят внешний вид дроби, но дробь останется равной данной.

Новизна этого раздела математики, а также его жизненно-практическая значимость вызывают у учащихся большой интерес. Это объясняется использованием при изучении дробей большого количества наглядных пособий, дидактического материала, акти­визацией практической деятельности учащихся.

Изучение обыкновенных дробей расширяет представление ум­ственно отсталых школьников о числах. Учащиеся узнают, что, кроме целых чисел, существуют еще и дробные, которые обладают особыми свойствами, отличными от свойств целых чисел, а изуче­ние арифметических действий с дробями убеждает их, что дроби, как и целые числа, можно складывать, вычитать, умножать, де­лить, что все действия над дробными числами подчиняются тем же законам, что и действия над целыми числами. На примере изучения дробей учитель имеет возможность показать то общее, что свойственно всем числам, и то особенное, что свойственно только дробным числам. Все это способствует развитию наблюда­тельности, внимания, формированию логического мышления, уме­ния находить причинные связи и т. д.

Изучение дробей способствует развитию речи, обогащению словаря учащихся новыми словами и выражениями: разделить на равные части, пополам, доля, дробь, смешанное число, числитель, знаменатель, сократить, привести к наименьшему общему знаме­нателю и др.

Велико для учащихся с нарушением интеллекта жизненно-практическое значение изучения дробей. С дробными числами в форме обыкновенных дробей учащимся приходится сталкиваться в школьных мастерских (столярной, слесарной, переплетной, швей­ной и т. д.), на производственной практике. Незнание дробей может задержать овладение профессией, затруднит ориентацию выпускников школы VIII вида в повседневной жизни.

На уроках, где учащиеся получают первоначальное представле­ние об образовании, преобразованиях, свойствах дробей и дейст­виях над ними, совершенно необходимо использовать достаточное количество наглядных пособий, дидактического материала. При этом учитель не только организует наблюдения учащихся, но и включает их в активную практическую деятельность с дидактичес­ким материалом, а затем углубляет и конкретизирует представле­ние о дробных числах при решении жизненно-практических задач. Например, выполняются такие задания: отпилить 1/2 (половину) доски, отогнуть 1/4 часть картонного листа для приготовления ко­робки, вырезать шесть шестых долей круга, сшить их и образо­вать донышко берета и т. д. Таким образом, доли ½, ¼, 1/6 конкре­тизируются в представлении учащихся.

Какие же наглядные пособия и дидактический материал целе­сообразно использовать при изучении обыкновенных дробей?

Это такие пособия: предме­ты, которые легко разделить на равные части, например: ябло­ко, торт, репа, арбуз, апельсин и т. д.; при делении этих пред­метов на части образуются доли, значительно отличаю­щиеся от целого, — это поло­вина, четверть яблока (апель­сина); макеты предметов или шара, разделенных на равные части;

фанерные, картонные, бумажные круги, разделенные на равные части;

квадраты, прямоугольники, полоски, разделенные на равные части (рис. 22);

классные счеты с вертикальными прутьями и набором долей единицы;

таблицы с рисунками предметов, кругов, квадратов, прямо­угольников, отрезков, разделенных на равные части;

таблицы с долями и названиями долей;

таблицы, иллюстрирующие сравнение обыкновенных дробей между собой, сравнение их с единицей, преобразования обыкно­венных дробей и действия над ними.

ПОЛУЧЕНИЕ ДРОБЕЙ

Первое представление о доле, которая получается путем деле­ния целого предмета на равные части, учащиеся должны получить уже в 5-м классе школы VIII вида.

Прежде чем начать деление целого на равные части, нужно создать такую ситуацию, при которой учащиеся могли бы убедить­ся в необходимости выполнения этой операции. Например, дав ученику одно яблоко, учитель говорит: «У тебя только одно ябло­ко. К тебе пришел товарищ, и ты хочешь вместе с ним съесть яблоко. Как в этом случае ты поступишь?» Ученик отвечает: «Яблоко нужно разделить (разрезать) пополам». Учитель поясня­ет: «Разрезать пополам — это значит разрезать на две равные части». В результате такого деления получаются две половины, или две вторые доли.

Далее надо, чтобы учащиеся сами производили деление целого (конфеты, яблока, батона хлеба, ленты, листа бумаги и т. д.) на две равные части. Целое можно на равные части разрезать, перегнуть, разломить и т. д., т. е. получить равные части разными способами.

Учащиеся должны убедиться, что при делении целого на две равные части его вторые доли, или половины, равны, половины, полученные от деления разных целых, не равны. Для этого, на­пример, учитель дает одному ученику большой синий круг, а другому — красный меньшего размера и просит разделить эти круги на две равные части. Затем он задает вопросы: «Сколько половин получилось? Равны ли между собой половины одного круга? Покажите, что половины (вторые доли) каждого круга равны (уча­щиеся накладывают половины круга). Сравните половины синего и красного кругов. Половина какого круга больше? Почему?»

Учащиеся должны хорошо понимать, что часть зависит от це­лого. Если предмет разделен на равные части, то эти части равны, но доли разных предметов, хотя эти предметы и были разделены на то же количество частей, не равны. Поэтому если целые пред­меты не равны, то не равны и их части. Половины одного предме­та не только сравниваются, но и прикладываются друг к другу, в результате чего учащиеся убеждаются, что при этом снова полу­чается целый предмет.

Аналогично рассматривается получение четвертых, восьмых и других долей.

При знакомстве с этими долями целесообразно использовать для получения долей прямоугольники, равнобедренные треуголь­ники, полоски, отрезки.

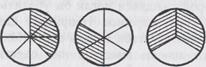
По возможности все виды работ учащихся с этими предметами надо отразить на страницах тетрадей: доли наклеить, отрезки начертить, полоски нарисовать, раскрасить. В итоге у учащихся формируется обобщение: если целое разделить на две, три, пять, десять и т. д. равных частей, а затем взять соответственно одну

часть, то взятыми окажутся третья, пятая, десятая и т. д. доли.

Следует также показать
учащимся разные способы де-
_Рис 23 ления квадрата и прямоуголь-

ника на равные части.

Далее учащиеся знакомятся с дробями (рис. 23). Дробь полу­чим, если возьмем одну или несколько долей какого-либо целого предмета, например одну, две, три, четыре, пять и т. д. долей круга (яблока, полоски и т. д.). Дроби читаются с помощью двух чисел. Первое число указывает на число долей, второе число показывает, на сколько равных долей разделили предмет (круг, квадрат, отрезок и т. д.). Например, три четвертых.

Одновременно необходимо показать и обозначение дробей на письме. Дроби обозначаются двумя числами: одна из них пишется

под горизонтальной чертой, а другая — над ней. Например, — одна вторая или половина; — две третьих и т. д.

Число, которое записано под чертой, показывает, на сколько равных долей разделили целое, — это знаменатель дроби. Число, которое записано над чертой, показывает, сколько таких частей взяли, — это числитель дроби.

Учащимся нужно показать, что условно целый предмет прини­мается за единицу (круг — это единица). Следовательно, если единицу разделить на несколько равных частей и взять одну или несколько таких равных частей, то получится дробь.

С учащимися необходимо проводить упражнения на закрепле­ние образования, чтения и записи дробей.

На этом же этапе обучения надо показать учащимся, что числа, полученные при измерении, могут быть записаны обыкно­венной дробью. Эти знания целесообразнее дать учащимся на примерах измерения длины.

Допустим, что при измерении карандаша или полоски получи­лось 10 см, или 1 дм. Вспомним, что в 1 м содержится 10 дм (показать метр, разделенный на дециметры). Следовательно,

1 дм= м, или 10 см=- м; 5 дм=50 см=- м; 50 см= м (если метр разделить пополам, то получится м, или 50 см). Если 1 м разделить на 4 равные части, то получится м; 20 см= м и т. д.

Учвщимся следует на доступных примерах показать, что дроби по­лучаются не только при нахождении длины, но и при измерении вре­мени, стоимости, при взвешивании, при измерении жидкостей и т. д., и поупоажняться в записи этих чисел обыкновенными дробями,

Школьники с нарушением интеллекта при выполнении деления целых чисел не раз убеждались, что не все числа делятся нацело, может получиться в частном остаток; деление же меньшего цело­го числа на большее целое невозможно. В то же время в повсе­дневной жизни они делили 3 яблока на 5 человек, 2 булочки на 3 равные части и т. д. Используя жизненный опыт учащихся, нужно показать, что при делении целого числа на целое получает­ся дробь. При этом деление возможно даже тогда, когда делимое меньше делителя.

Объяснить получение обыкновенной дроби путем деления целого на целое необходимо путем решения задачи жизненно-практического содержания. Например, нужно разделить две кон­феты между тремя мальчиками. Как это сделать? Возьмем одну конфету и разделим ее на 3 равные части. Каждый получит по -j доле. Затем вторую конфету разделим тоже на 3 равные части. Каждый получит еще по доле. Сколько же получил каждый мальчик? Каждый мальчик получил по 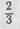конфеты (ученики это должны видеть). Запишем: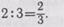

Со сравнением дробей можно познакомить учащихся, широ­ко используя их знания и опыт в получении дробей путем деления целого предмета (единицы) на равные части. Берем яблоко, делим его на 4 равные доли. Сравним долю яблока и Что больше: ' Учащиеся наглядно убеждаются в том, чтоТак же

сравниваются Учитель обращает внимание на знаме-

натели и числители сравниваемых дробей. Учащиеся, наблюдая, убеждаются, что среди дробей с одинаковыми знаменателями дробь с большим числителем оказывается бштьшрй.

Затем учитель пишет ряд дробей с одинаковыми

знаменателями, но разными числителями и просит рассказать и показать, как получить эти дроби, используя полоски бумаги или отрезки. Он обращает внимание учащихся сначала на знаменатели всех записанных дробей (знаменатели всех дробей одинаковые), а затем на их числители (числители разные) и с помощью чертежа просит сравнить эти дроби. Так учащиеся подводятся к обобщению, что при одинаковых знаменателях та дробь больше, у которой чис­литель больше. Для вывода правила необходимо рассмотреть (на круге, дробных счетах, квадрате) еще ряд дробей с одинаковыми знаменателями, но разными числителями и сравнить их.

Такие упражнения позволят уча­щимся сознательно усвоить прави­ло сравнения дробей с одинаковы­ми знаменателями. Во всех случаях следует подчеркивать и останавли­вать внимание учащихся на том, что доли, которые сравниваются, одинаковые, но количество этих долей разное. Следовательно, чем больше долей, тем дробь больше. Далее учащимся можно предлагать задания более отвлеченного

характера, например такие: сравнить следующие дроби:

записать их от меньшей к большей (и наоборот); назвать наименьшую (наибольшую) дробь из данного ряда дробей; назвать из данного ряда дробей дроби меньше

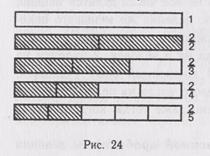
Чтобы предупредить формальное усвоение учащимися знаний по этой теме, механическое использование правил сравнения дро­бей, необходимо время от времени требовать от учащихся изобра­жения и сравнения дробей на рисунках (рис. 24)

В это время целесообразно научить учащихся сравнивать дроби с единицей и на основе этих знаний дать понятие о правильной и неправильной дроби. Например, следует выполнить задание: пока­зать образование дробей на отрезках, полосках, кругах; 298

ответить на вопрос, какие из дробей меньше единицы, какие равны 1, какие больше 1.

Правильные и неправильные дроби. Смешанное число

Представление о правильных и неправильных дробях формиру­ется на основе использования наглядности и практической дея­тельности учащихся.

Учащимся предлагается взять целый круг (единицу), разделить

его на равные части, взять одну четвертую часть, затем две

четверти, три четверти и сравнить полученные части (дроби) с целым кругом (с единицей). В итоге ученики убеждаются в том, что эти дроби меньше единицы. Подобное сравнение про­водится и на других пособиях: квадратах, полосках, отрезках.

Учащиеся получают дроби: и др. Учитель

каждый раз подчеркивает, что эти дроби меньше единицы, одно­временно обращая внимание на то, что числители всех этих дро­бей меньше знаменателя. На основе многократных наблюдений, практической деятельности учащиеся подводятся к обобщению: дробь, меньшая единицы, называется правильной дробью. Числи­тель и знаменатель правильных дробей учащимся предлагается сравнить самим. Наиболее сильные учащиеся самостоятельно могут сделать вывод: у правильной дроби числитель всегда мень­ше знаменателя.

Аналогичными приемами учащиеся знакомятся с образованием неправильной дроби и подводятся к ее определению. Им предлага­ется взять четыре равные доли того круга, который они разделили

на 4 равные части. Получилась дробь Если четвертые доли приложить друг к другу, то образуется целый круг, т. е. единица. Таким образом, учащиеся убеждаются, что равны 1 (единице).

Затем учитель демонстрирует два круга, разделенные на 4 рав­ные части; одновременно учащиеся берут 2 равных по размеру круга и делят каждый на 4 равные части.

Последовательно учитель показывает, а учащиеся откладывают на партах одну, две, три и т. д. четвертые доли. Одновременно даются названия взятому числу долей, сравниваются числители и

знаменатели: Дроби 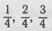правильные. Они

меньше единицы. Дробь равна 1. Дроби больше едини-

цы. Сравниваются по величине числители и знаменатели этих дробей, и учащиеся подводятся к выводу правила: дроби, которые равны или больше единицы, называются неправильными дробя­ми. У неправильной дроби числитель равен или больше знамена­теля. Далее проводятся упражнения на дифференциацию правиль­ных и неправильных дробей. Например, такие: 1) начертить отре­зок, разделить его на 6 равных частей, написать все дроби, кото­рые получились, указать правильные дроби; 2) начертить две по­лоски, равные по длине, каждую полоску разделить на 5 равных частей, записать отдельно правильные и неправильные дроби; 3) на­писать правильные, а затем неправильные дроби с данными знамена­телями: 4) написать неправильные, а затем правиль­ные дроби с данными числителями: 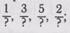5) из ряда дробей

выписать сначала только правильные дро­би, а затем дроби, равные единице (как называются дроби, равные единице?); 6) записать 5 правильных и 5 неправильных дробей, объяснить, как получилась каждая дробь; 7) используя таблицы с изображением предметов, разделенных на несколько равных час­тей, записать или назвать все дроби, а затем выделить из них правильные и неправильные.

Понятие смешанного числа следует также формировать с помо­щью наглядных пособий, дидактического материала, а главное, с помощью практической деятельности с этим материалом самих учащихся, их жизненного опыта.

Например, можно предложить такие задачи:

«Купили целую буханку хлеба и еще половину буханки. Сколь­ко купили хлеба?»

Смешанное число записывается целым числом и дробью.

Не нашли, что искали? Воспользуйтесь поиском: