
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
СРАВНЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ
Начинать сравнение десятичных дробей следует с дробей со знаменателем 10, например 0,3 и 0,5. Сначала нужно каждую из этих дробей показать на метровой линейке, разделенной на дециметры. Известно, что
1 дм — это 0,1 м 9 дм<5 дм, значит,
3 дм — это 0,3 м 0,3 м<0,5 м
5 дм — это 0,5 м 0,3<0,5
Далее следует каждую из этих дробей сравнить с помощью любого отрезка (рис. 28). 0,3
0,5
Рис. 28
Легко сравнить эти десятичные дроби, если записать их со знаменателями: 5/10 и 3/10. Как сравнивать обыкновенные
обыкновенные дроби с одинаковыми знаменателями, учащиеся знают.
После рассмотрения еще нескольких пар десятичных дробей на конкретных примерах можно подвести учащихся к выводу: из сравниваемых десятичных дробей та дробь больше, у которой число целых больше; если же целые равны (например, в дробях 0,3 и 0,5), то сравниваются десятые доли, и тогда та дробь больше, у которой число десятых долей больше.
По аналогии с десятичными дробями со знаменателем 10 сравниваются десятичные дроби со знаменателем 100 (0,08 и 0,05) и со знаменателем 1000 (0,007 и 0,004).
В качестве пособий для сравнения дробей со знаменателем 100 можно использовать метр, деленный на сантиметры, или квадрат, деленный на 100 клеток:
| 0,008 >0,005 0,08>0,05 |
1 см=0,01 м 8 см=0,08 м 5 см=0,05 м
После усвоения этого материала для сравнения можно предъявлять десятичные дроби с различными знаменателями:
| 0,7 и 0,13 0,08 и 0,1 |
0,08 и 3,1 7,3 и 7,119
Если учащиеся затрудняются сравнивать дроби, то следует прибегнуть к использованию наглядных пособий, которыми в данном случае служат меры длины, стоимости, массы, а также отрезки и квадраты, или привести дроби к общему знаменателю. Сравнивать нужно равные десятичные дроби, но имеющие различное написание, например: 0,3 и 0,30. Что эти дроби равны, учащиеся могут убедиться с помощью метровой линейки или квадрата, разделенного на 100 равных клеток.
| 0,3 м = 3 дм |
Отсюда следует, что 0,3=0,30.
0,30 м = 3 дм]
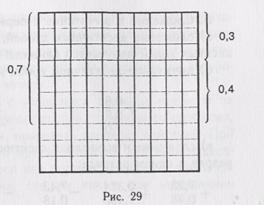
0,1=0,10 (так как каждая полоса — это 0,1, а каждая клетка — это 0,01); 0,3=0,30; 0,5=0,50 и т. д.
На подобных примерах учащиеся убеждаются, что десятые доли могут быть выражены в сотых и, наоборот, сотые — в десятых долях. Это закрепляется с помощью упражнений, например таких:
Сколько десятых долей в 1 м? Чему равна одна десятая доля метра? Сколько сотых долей в 1 м? Чему равны 10 сотых метра?
0,1 м=0,10 м 0,1=0,10
Чему равны 4 десятых метра? Чему равны 40 сотых метра?
0,4 м=0,40 м 0,4=0,40
Сколько десятых в 0,1; в 0,10? Сколько десятых в 0,8; в 0,80?
Сравнение сотых и тысячных, десятых и тысячных долей проводится так же, как сравнение десятых и сотых долей. На конкретных примерах (с мерами длины, стоимости, массы), а затем и путем отвлеченных рассуждений учащиеся убеждаются, что, например, 0,1=0,10=0,100; 0,7=0,70=0,700 и т. д. и, наоборот, 0,10=0,1; 0,70=0,7 и т. д.
Учитель обращает внимание учащихся на то, что нули, приписанные в долях дроби справа от значащей цифры, не влияют на дробь. Отсюда можно подвести учащихся к понятию о сокращении десятичных дробей.
Сокращение десятичных дробей
На примерах и практических упражнениях с метровой линейкой, квадратом, разделенным на 100 равных квадратов и 10 равных полос, учащиеся убедились, что если дробь, например 0,30, записать без нуля справа, т. е. 0,3, то дробь не изменится, но она примет более простой вид: 0,30=0,3. Запишем 0,30 со знаменателем:  Сократим эту дробь на 10, получим дробь
Сократим эту дробь на 10, получим дробь 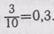
Допустим дана дробь 1,70. Эту дробь учащимся можно показать на рулетке: 1 м 70 см, или 1,70 м, но это и 1 м 7 дм, т. е. 1,7 м, значит, 1,7 м=1,70 м, а теперь эти дроби запишем без наименований 1,70=1,7. Учащиеся еще раз убеждаются, что если в десятичной дроби отбросить 0 после значащей цифры, то величина этой дроби не изменяется.
Далее объясняем сокращение десятичной дроби, опираясь на знания учащихся о сокращении обыкновенной дроби.
Допустим, надо сократить дробь 1,70. Вначале учащиеся записывают эту дробь со знаменателем, а затем сокращают ее:
Следовательно, отбрасывая один нуль после значащей цифры, мы сокращаем дробь на 10 (соответственно объясняем, что если отбрасываются два нуля, то дробь сокращается на 100:

Приведение десятичных дробей к общему знаменателю
Учащиеся уже умеют сравнивать десятичные дроби, знают правило сравнения дробей по разрядам, но легче сравнивать дроби тогда, когда они выражены в одних и тех же десятичных долях, т. е. имеют
12 Перова М. Н. 325
общий знаменатель. Например, дроби 0,50 и 0,35 имеют общий знаменатель 100: 0,50>0,35, так как 50 сотых больше 35 сотых. Для удобства вычислений дроби также выражают в одинаковых долях, т. е. приводят к наименьшему общему знаменателю.
Учащиеся знают, что нуль, приписанный справа, дроби не изменяет, т. е. 0,3=0,30=0,300. Увеличивая числитель, мы одновременно во столько же раз увеличиваем знаменатель.
Допустим, даны две дроби 0,2 и 0,40, их надо выразить в одинаковых долях. Это значит, что дробь 0,2 надо выразить в сотых долях: 0,2=0,20. Дроби 0,20 и 0,40 имеют одинаковый знаменатель 100. Значит, надо уравнять после запятой число знаков (цифр) путем приписывания нулей справа. Так же выражают в одинаковых долях дроби 5,6 и 0,75. Общий знаменатель этих дробей 100. Дроби 5,6 и 0,75 теперь будут выглядеть так: 5,60 и 0,75.
В целях дифференциации понятий выразить дроби в одинаковых долях и выразить дроби в более крупных долях предлагаются упражнения вида:
1) сократить дроби: 110,80; 10,800; 4,40; 25,070;
2) привести дроби 10,8 и 10,83; 14,1 и 18,206; 17,85 и 41,063;
63,486 и 1,08 к общему знаменателю;
3) сократить дроби: 10,80; 10,830; 14,10; 15,040; 80,900;
71,060; 20,700.
Запись чисел, полученных при измерении величин, в виде десятичной дроби
В быту, в учебных мастерских и на производственных предприятиях учащимся приходится сталкиваться с выражением чисел, обозначающих длину, массу, стоимость и другие величины, десятичной дробью и наоборот. Начать изучение этой темы следует с выражения мер длины стоимости и массы десятичной дробью и наоборот. Например, 1 дм — это одна десятая доля метра, следовательно, 1 дм=0,1 м. На основании этого можно составить такую табличку:
1 дм=0,1 м
2 дм=0,2 м
5 дм=0,5 м
15 дм =1,5 м, так как 10 дм — это целый метр.
По аналогии с этим можно провести рассуждения и записать десятичными дробями числа, выраженные в других мерах. Например:
| 1 к.=0,01 р. 2 к.=0,02 р. 15 к.=0,15 р. 125 к.= 1,25 р. |
1 г=0,001 кг
5 г=0,005 кг
18 г=0,018 кг
235 г=0,235 кг
При записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью следует соблюдать определенную последовательность, учитывая степень трудности выражения этого числа десятичной дробью. Вначале следует предлагать учащимся числа, выраженные одной единицей мер длины, стоимости, массы и др., а затем — двумя, причем вначале единичное отношение мер должно равняться 10. Например:
| 2 дм =0,2 м 3 см=0,3 дм 7 мм=0,7 см |
3 м 5 дм=3,5 м
7 дм 5 см=7,5 дм
1 см 8 мм=1,8 см и т. д.
Затем надо брать такие числа, где единичное отношение мер равно 100. Например:
| 1 м 12 см=1,12 м 8 р. 75 к. = 8,75 р. 3 ц 8 кг=3,08 ц |
1 см=0,01 м 5 к.=0,05 р. 25 к.=0,25 р.
Наконец, берутся такие числа, где единичное отношение мер равно 1000. Например:
| 1 м=0,001 км 2 г=0,002 кг 15 кг=0,015 т |
17 км 350 м= 17,350 км 3 кг 725 г=3,725 кг 8 т 600 кг=8,600 т
Особое внимание обращается на такие случаи записи чисел, обозначающих длину, стоимость, массу и др., десятичной дробью, в которых в десятичной дроби десятичные доли разряда равны нулю. Например, при записи десятичной дробью следующих чисел: 8 к., 5 р., 6 к., 3 м 4 см, 7 км 80 м, 8 т 30 кг. Записывается так: 8 к.=0,08 р., так как 1 к.=0,01 р. 5 р. 6 к.=5,06 р.; 3 м 4 см= =3,04 м, 7 км 80 см=7,080 км=7,08 км; 8 т 30 кг=8,030 т=8,03 т.
Запись десятичной дроби числами, полученными от измерения величин
В практике нередко требуется десятичную дробь записать в виде целого числа с одним или двумя наименованиями мер. Чтобы учащиеся могли выполнить это преобразование, необходимо использование наглядных пособий и соблюдение определенной последова-
12* 327
|
| 3. Сложение и вычитание десятичных дробей с одинаковым числом знаков без перехода через разряд: 0,3+0,4 0,14+1,25 7,4-1,3 3,42-1,31 3,124+7,835 4,356-2,135 |
тельности. Сначала следует вспомнить соотношение единиц мер и рассмотреть те десятичные дроби, которые имеют знаменатель 10.
| 1 м=10 дм 0,1 м = 1 дм 0,5 м=5 дм 1,7 м = 1 м 7 дм |
1 дм=10 см
0,1 дм = 1 см
0,3 дм=3 см
10,4 дм=10 дм 4 см
Затем рассматриваются дроби со знаменателями 100, 1000, т. е. с сотыми и тысячными долями. Например: 0,8 р.=80 к.; 2,5 м=250 см; 0,3 кг=300 г.
Не нашли, что искали? Воспользуйтесь поиском: