Умножение десятичной дроби на 10, 100, 1000

При выводе правила об умножении десятичной дроби на 10, 100, 1000 целесообразнее всего опираться на знания учащихся об умножении обыкновенных дробей.

Например: 0,7x10=? Учитель, опираясь на знания учащихся, просит записать первый множитель со знаменателем, т. е. обыкно­венной дробью, и произвести умножение: 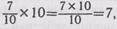сле­довательно, 0,7x10=7. Затем учитель обращает внимание уча­щихся на первый множитель и на произведение (0,7 и 7) и просит сравнить их. Он спрашивает: «Что произошло с запятой во мно­жителе, когда его умножили на 10? В какую сторону и на сколько знаков переместилась запятая во множителе при умножении на 10?»

Затем надо рассмотреть еще один пример и снова ответить на вопрос о перемещении запятой вправо после умножения десятич­ной дроби на 10: 1,23-10=?

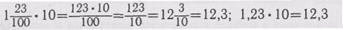
После рассмотрения еще двух-трех примеров и сравнения мно­жителя и произведения некоторые учащиеся сами могут сделать вывод: при умножении десятичной дроби на 10 нужно перенести запятую вправо на один знак.

Объяснение можно провести, используя нумерационную табли­цу. Запишем 0,7 в таблицу. Это число надо умножить на 10, т. е. увеличить в 10 раз. Это значит, надо передвинуть данное число в нумерационной таблице на один разряд влеж>, будет 7. Решив таким способом еще ряд примеров, учащиеся придут к выше сформулированному правилу. Аналогично рассматривается умно­жение десятичной дроби на 100, 1000.

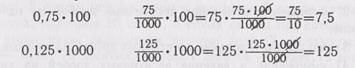
После того как ученики усвоят правило умножения на 10, 100, 1000, необходимо подвести их к выводу общего правила умножения десятичной дроби на единицу с нулями: при умножении десятичной дроби на число, выраженное единицей с нулями, нужно перенести вправо запятую на столько знаков, сколько нулей в множителе.

Учителю обязательно надо обратить внимание учащихся на то, что при умножении числа на 10, 100, 1000 каждый разряд произ­ведения соответственно увеличивается в 10, 100, 1000 раз. Напри­мер: 7,95-10=79,5. Сопоставляя первый множитель и произведе­ние, надо показать, что 7 единиц множителя увеличились в 10 раз и в произведении получилось 7 десятков, 9 десятых увеличились тоже в 10 раз и в произведении получилось 9 единиц, 5 сотых увеличились в 10 раз и в произведении получилось 5 десятых.

Аналогично рассматриваются примеры на умножение десятичной дроби на 100, 1000.

Особое внимание нужно обратить на такие случаи умножения, в которых в результате умножения десятичной дроби на 10, 100 или 1000 в ответе получается целое число (учащиеся недоумева­ют: умножали дробь, а получилось целое число).

Еще большую трудность вызывает решение таких примеров, в которых в произведении нужно приписывать нули справа — число знаков после запятой меньше, чем число нулей во втором множителе, например: 0,5'100=50.

Для того чтобы учащиеся более осознанно относились к реше­нию подобных примеров, нужно время от времени сравнивать разряды первого множителя и произведения, например: 0,15-10=1,5. Рассуждать следует так: «Одну десятую увеличили в 10 раз, получили одну целую, пять сотых увеличили в 10 раз, получили пять десятых».

Полезны и такие упражнения:

Если в числе 4,54 перенести запятую вправо на один знак, то число примет вид 45,4 Что же произошло с этим числом? Во сколько раз увеличилось это число? Что произошло с единицами (с десятыми, сотыми долями)?

Если в числе 3,75 перенести запятую на два знака вправо, то что произойдет с числом? Во сколько раз увеличится число? Во сколько раз увеличится каждый разряд этого числа?

Если число 4,8 увеличить в 1000 раз, то для этого нужно перенести запятую на три знака вправо, но в первом множителе после запятой только один знак. В этом случае следует рекомен­довать учащимся поставить три точки после запятой, например: 4,8x1000=48, а затем на месте точек написать нули: 4,8-1000=4800.

Деление десятичной дроби на 10, 100, 1000

Деление десятичной дроби на 10, 100, 1000 рассматривается аналогично умножению (десятичные дроби записываются со зна­менателем):

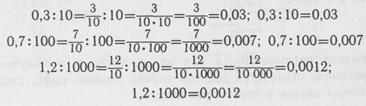
Сначала делается вывод о делении десятичной дроби на 10, затем на 100 и затем на 1000. В итоге учащиеся подводятся к общему правилу деления десятичной дроби на число, выраженное единицей с нулями.

Так же как и при умножении десятичных дробей, обращается внимание на то, что при делении числа на 10, 100, 1000 каждый разряд частного уменьшается соответственно в 10, 100, 1000 раз.

Учитывая, что при умножении и делении десятичных дробей на 10, 100, 1000 умственно отсталые школьники допускают много ошибок, в частности путают, куда переносить запятую — влево или вправо, необходимо чаще решать примеры, в которых бы действия умножения и деления сопоставлялись, например: 7,85-10=78,5; 78,5:10=7,85; 78,5-100=7850; 78,5:100=0,785.

Полезно, так же как и при умножении, ставить перед запятой (слева от запятой) столько точек, сколько нулей в делителе,.7,45:100=0,0745.

Не нашли, что искали? Воспользуйтесь поиском: