
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
МЕТОДИКА ИЗУЧЕНИЯ ПРОЦЕНТОВ
Понятие о проценте дается учащимся специальной школы VIII вида после изучения десятичных дробей. Процент — это дробь
со знаменателем 100, имеющая особое название (подобно -^ — половина) и особую форму записи (1/100 — процент). Слово «процент» обозначается знаком %.
Десятичные дроби со знаменателем 100 наиболее удобны для вычислений, так как во многих мерах метрической системы встречается единичное отношение 100 (1 м=100 см, 1 р. = 100 к., 1 га=100а, 1 ц=100кг; следовательно, 1 см=0,01 м, 1 к.=0,01 р.,
1 а=0,01 га, 1 кг=0,01 ц),1/100 часть числа обозначается так: 1%.
Можно записать, что 1 см=0,01 м=1% метра, 1 к.=0,01 р. = 1% рубля, 1а=0,01 га=1% гектара, 1 кг=1% центнера. В данном случае мы выразили полученные числа в процентах. Отвлеченные
числа также можно выразить в процентах. Учащимся это можно объяснить так: «1% — это -щ часть числа. Чему же равно все
число? Оно в 100 раз больше, т. е.  Значит,
Значит,
если 

|
15=1500%» и т. д.
На основе понятия о проценте и умений выразить (записать) числа в процентах необходимо объяснить значение часто встречающихся на производстве и в быту выражений, например: «Рабочий выполнил норму по обработке деталей на 100%». Это означает, что рабочий обработал за смену то количество деталей, которое было запланировано, например 150 деталей. Если рабочий сделал меньше 150 деталей, то он не выполнил норму, т. е. выполнил ее меньше чем на 100%. Если рабочий сделал больше 150 деталей, то он перевыполнил норму, т. е. выполнил ее больше чем на 100%.
Учащиеся знакомятся не только с выражением целого числа, но и десятичных дробей процентами.
В этом случае учитель при объяснении также исходит из определения процента: 0,01 = 1%, следовательно,  ;;
;;  , На основании подобных рассуждений, наблюдений и сравнения десятичной дроби и числа, выражающего эту дробь в процентах, некоторые учащиеся могут сделать вывод: чтобы десятичную дробь заменить процентами, надо перенести запятую вправо на два знака и поставить знак %. Вместо недостающих знаков ставятся нули. Обыкновенную дробь также можно выразить (заменить) процентами. Ее нужно для этого обратить в десятичную дробь и применить правило замены десятичной дроби процентами.
, На основании подобных рассуждений, наблюдений и сравнения десятичной дроби и числа, выражающего эту дробь в процентах, некоторые учащиеся могут сделать вывод: чтобы десятичную дробь заменить процентами, надо перенести запятую вправо на два знака и поставить знак %. Вместо недостающих знаков ставятся нули. Обыкновенную дробь также можно выразить (заменить) процентами. Ее нужно для этого обратить в десятичную дробь и применить правило замены десятичной дроби процентами.
Учащихся школы VIII вида знакомят и с обратной задачей: выражением процентов в десятичных или обыкновенных дробях.
Рассуждения ведутся также исходя из понятия о проценте:

На основе наблюдений и сравнения числа процентов и дроби, выражающей это число, учащиеся подводятся к выводу: чтобы выразить проценты десятичной дробью или целым числом, надо запятую перенести на два знака влево и знак % не писать: 20% =0,2; 300%=3.
Решение задач на проценты
Программой школы VIII вида предусмотрено решение задач на нахождение одного и нескольких процентов от числа, а также нахождение числа по одному проценту.
Задачи на проценты не представляют собой ничего нового для учащихся по сравнению с ранее решавшимися задачами на нахождение одного и нескольких частей от числа и на нахождение числа по одной и нескольким частям. Поэтому, прежде чем решать задачи на проценты, надо повторять решение ранее решавшихся задач и довести до сознания каждого учащегося, что
1 % — это тоже дробь, но записанная особым
образом. 
Сначала дается понятие вычисления 1 % и нескольких процентов от числа и вырабатывается навык выполнения этих действий.
Учащиеся должны решить несколько таких примеров и на основе наблюдений сделать вывод: чтобы найти 1% от числа, надо это число разделить на 100. Только после этого учащиеся начнут решать задачи на нахождение 1 % от числа типа: «Рабочий получает 1000 р. 1% от своего заработка он платит налог. Сколько денег рабочий платит?»

Аналогично подходят и к решению задач на нахождение нескольких процентов от числа. Например, надо найти 5% от 200,
т. е. -г™ от 200. Находим сначала 1%, т. е. 1/100 долю от 200.
(200:100-1=2), и берем 5 таких долей, т. е. 5%. Значит, 2 •5=10. Вычисления записываются так: 200:100 «5= 10.
Учитель обязательно должен каждый раз спрашивать: «Что мы получаем, когда делим число на 100? Почему умножаем на число процентов?» Это позволяет учащимся более сознательно относиться к вычислениям.
Задачи на нахождение нескольких процентов от числа целесообразно решать сначала в два действия и только тогда, когда учащиеся осознанно будут относиться к записи решения задачи сложным примером, содержащим два действия, можно будет записать действия в одну строку. Например: «В школу привезли 700 учебников. 9% учебников передали в библиотеку. Сколько учебников передали в библиотеку?»
| 2-й способ записи решения. 1. Сколько учебников передали в библиотеку? 700 уч.: 100-9=63 уч. Ответ. 63 учебника передали в библиотеку. |
1-й способ записи решения.
1. Чему равен 1% от числа
700 учебников?
700 уч.: 100=7 уч.
2. Сколько учебников переда
ли в библиотеку?
7 уч.-9=63 уч. Ответ. 63 учебника передали в библиотеку.
Задачи на нахождение 1% от числа и на нахождение нескольких процентов от числа необходимо постоянно сопоставлять, находить черты сходства и различия.
Задачи на нахождение числа по одному проценту обрат-ны задачам на нахождение 1% и нескольких процентов от числа. Поэтому нужно сначала рассмотреть прямую задачу, решить ее, а потом из нее образовать обратную ей задачу, решить ее и сопоставить решение прямой и обратной задач.
Прямая задача: «В саду посадили 200 саженцев фруктовых деревьев. 1 % саженцев погиб. Сколько саженцев фруктовых деревьев погибло?» 1% от 200 — это 200:100=2 (саж.).
Обратная задача: «В саду посадили саженцы фруктовых деревьев. 2 саженца погибло, что составляет 1 % от всех посаженных деревьев. Сколько саженцев фруктовых деревьев посадили в саду?»
Рассуждение проводим так: «2 саженца — это 1% всех деревьев, а все саженцы составляют 100%, т. е. их число в 100 раз больше 2, поэтому нужно 2 • 100. Следовательно, если 1 % составляет 2 саженца, то 100% составляет 2«100=200 (саженцев)».
Решив еще несколько аналогичных задач и примеров на нахождение числа по одному проценту и сопоставив их с прямыми задачами и примерами, можно подвести учащихся к выводу: чтобы найти число по 1%,нужно это число умножить на 100.
Часто встречаются задачи, в которых нужно вычислить число процентов, превышающих 100%. Эти задачи имеют большое жизненно-практическое значение и часто встречаются.
Например: «Норма выработки рабочего — 400 деталей за смену. Он выполнил норму на 115%. Сколько деталей он сделал?»
Находим 115% от 400. 400 дет.: 100-115=460 дет. Ответ. Рабочий сделал за смену 460 деталей.
Задачу можно решить и другим способом. Рассуждаем так: 400 деталей — это 100%. Рабочий выполнил норму на 115%, т. е. он перевыполнил план на 15% (115% —100% = 15%). Найдем, сколько деталей рабочий сделал сверх плана. Надо найти 15% от 400 деталей. 400 дет.: 100» 15=60 дет. Далее узнаем, сколько деталей сделал рабочий за смену: 400 дет.+60 дет.=460 дет.
Ответ. Рабочий сделал за смену 460 деталей. 342
Вопросы и задания
1. Опираясь на программу, укажите, над формированием каких понятий
по теме «Десятичные дроби» вы будете работать на уроках математики в
старших классах специальной школы VIII вида.
2. Как расширяются представления учащихся о десятичной системе счис
ления при изучении нумерации десятичных дробей? Начертите таблицу клас
сов и разрядов.
3. Составьте фрагмент одного из уроков, на котором учащиеся получают
понятие о десятичной дроби, сокращении десятичной дроби, приведении
десятичных дробей к наименьшему общему знаменателю.
4. Приведите примеры приемов активизации познавательной деятельности
учащихся в процессе изучения действий с десятичными дробями.
5. Составьте упражнения разных видов для закрепления навыков вычис
ления с десятичными дробями. Продумайте систему коррекционной работы
при использовании этих упражнений.
Глава 19
МЕТОДЛКА РЕШЕНИЯ АРИФМЕТИЧЕСКИХ ЗАДАЧ
Арифметические задачи в курсе математики в школе VIII вида занимают значительное место. Почти половина времени на уроках математики отводится решению задач. Это объясняется большой коррекционно-воспитательной и образовательной ролью, которую они играют при обучении школьников с нарушением интеллекта.
Решение арифметических задач помогает раскрыть основной смысл арифметических действий, конкретизировать их, связать с определенной жизненной ситуацией. Задачи способствуют усвоению математических понятий, отношений, закономерностей. В этом случае они, как правило, служат конкретизации этих понятий и отношений, так как каждая сюжетная задача отражает определенную жизненную ситуацию.
При решении задач у умственно отсталых школьников развивается произвольное внимание, наблюдательность, логическое мышление, речь, сообразительность. Решение задач способствует развитию таких процессов познавательной деятельности, как анализ, синтез, сравнение, обобщение.
В процессе решения арифметических задач учащиеся учатся планировать и контролировать свою деятельность, овладевают приемами самоконтроля (проверка задачи, прикидка ответа, решение задачи разными способами и т. д.), у них воспитывается настойчивость, воля, развивается интерес к поиску решения задачи.
Велика роль решения задач в подготовке умственно отсталых учащихся к жизни, к их дальнейшей трудовой деятельности. Именно упражнения в решении и составлении задач помогают учащимся видеть в окружающей действительности такие факты и закономерности, которые используются в математике. При решении сюжетных задач учащиеся учатся переводить отношения между предметами и величинами на «язык математики».
В арифметических задачах используется числовой материал, отражающий успехи нашей страны в различных отраслях народного хозяйства, культуры, науки и т. д. Это способствует расширению кругозора учащихся, обогащению их новыми знаниями об окружающей действительности.
Обучая самих учащихся «добывать» числовой материал для составления задач, учитель имеет возможность показать учащимся, что задачи ежедневно ставит сама жизнь и уметь решать
такие задачи — значит подготовить себя к ориентировке в окружающей действительности.
Решение арифметических задач на уроках математики позволит реализовать задачу подготовки учащихся к более успешному овладению профессиональным трудом, сблизить обучение с жизнью.
Умением решать арифметические задачи учащиеся овладевают с большим трудом.
Анализ контрольных работ учащихся, наблюдения и специальные исследования показывают, что ошибки, которые учащиеся допускают при решении задач, можно классифицировать так:
1. Привнесение лишнего вопроса и действия.
2. Исключение нужного вопроса и действия.
3. Несоответствие вопросов действиям: правильно поставлен
ные вопросы и неправильный выбор действий или, наоборот, пра
вильный выбор действий и неверная формулировка вопросов.
4. Случайный подбор чисел и действий.
5. Ошибки в наименовании величин при выполнении действий:
а) наименования не пишутся; б) наименования пишутся ошибоч
но, вне предметного понимания содержания задачи; в) наименова
ния пишутся лишь при отдельных компонентах.
6. Ошибки в вычислениях.
7. Неверная формулировка ответа задачи (сформулированный
ответ не соответствует вопросу задачи, стилистически построен
неверно, не соответствует ответу последнего действия и т. д.).
Причины ошибочных решений задач умственно отсталыми школьниками кроются в первую очередь в особенностях мышления этих детей.
Трудности в решении задач у умственно отсталых учащихся связаны с недостаточным пониманием предметно-действенной ситуации, отраженной в задаче, и математических связей и отношений между числовыми данными, а также между данными и искомыми.
Опыт показывает, что школьники с нарушением интеллекта справляются с решением задач, если они составлены на основе действий с реальными предметами. Основные трудности возникают тогда, когда необходимо наглядно представить словесно сформированные задачи. В их сознании не всегда возникает отражение действительного содержания ситуации и заключенных в ней предметных отношений. Понимание условия задачи нередко не отвечает ее предметному содержанию.
13 Перова М. Н.
При решении задач учащиеся не фиксируют свое внимание на математических отношениях, с учетом которых должны выполняться действия.
Поверхностный анализ содержания задачи приводит к отклонению от конечной цели. Школьники с нарушением интеллекта не осознают условия задачи, изменяют и упрощают его. Нередко при воспроизведении текста задачи они привносят в условие штампы и руководствуются ими при решении, а действительные связи и отношения не учитывают, опираются на фрагменты или несущественные элементы задачи, при выборе действий руководствуются словами всего, меньше, больше, осталось. В силу стереотипности действий, характерной для умственно отсталых учащихся, они решают задачи шаблонными способами, руководствуясь случайными ассоциациями, вызванными созвучием слов и выражений. Уподобление одних задач другим — наиболее часто встречающийся вид ошибок, так как осознание сходства и различия арифметических задач представляет для учащихся с нарушением интеллекта наибольшую трудность.
Знание особенностей решения задач умственно отсталыми учащимися помогает учителю избрать наиболее целесообразные пути, методы и приемы преодоления трудностей.
В процессе обучения решению задач следует избегать натаскивания в решении задач определенного вида, надо учить сознательному подходу к решению задач, учить ориентироваться в определенной жизненной ситуации, описанной в задаче, учить осознанному выделению данных и искомого задачи, установлению взаимосвязи между ними, осознанному выбору действий.
Сознательному подходу к решению любой задачи умственно отсталых школьников необходимо обучать последовательно и терпеливо, формируя у них определенные умственные действия.
В методике работы над любой арифметической задачей можно выделить следующие этапы: 1) работа над содержанием задачи; 2) поиск решения задачи; 3) решение задачи; 4) формулировка ответа; 5) проверка решения задачи; 6) последующая работа над решенной задачей.
Работа над содержанием задачи
Большое внимание следует уделять работе над содержанием задачи, т. е. над осмыслением ситуации, изложенной в задаче, установлением зависимости между данными, а также между данными и искомым. Последовательность работы над усвоением со-
держания задачи: а) разбор непонятных слов или выражений, которые встретятся в тексте задачи; б) чтение текста задачи учителем и учащимися; в) запись условия задачи; г) повторение задачи по вопросам; д) воспроизведение одним из учащихся полного текста задачи.
Работа над отдельными словами и выражениями должна вестись не тогда, когда учитель знакомит учащихся с содержанием задачи, а раньше, до предъявления задачи, иначе словарная работа разрушает структуру задачи, уводит учащихся от понимания арифметического содержания задачи, зависимости между данными.
Текст задачи первоначально рассказывает или читает учитель, а начиная со 2-го класса его могут читать и ученики по учебнику или по записи на доске. Читать задачу нужно выразительно, выделяя голосом математические выражения, главный вопрос задачи, делая логические ударения на тех предложениях или сочетаниях слов, которые прямо указывают на определенное действие (например, разложили поровну в две вазы, купили 3 тетради по 12 р. за каждую). Между условием задачи и вопросом следует сделать паузу, если вопрос стоит в конце задачи.
Выразительному чтению текста задачи следует учить учеников. Нужно помнить, что школьники с нарушением интеллекта, если их этому специально не учить, не могут самостоятельно правильно прочитать задачу, не могут расставить логические ударения, даже выделить вопрос задачи, если он стоит в начале или середине задачи.
Восприятие текста задачи только на слух на первых порах невозможно для школьников с нарушением интеллекта, они воспринимают нередко только фрагменты задачи, с трудом вычленяют числовые данные. При первом чтении они в основном запоминают лишь повествовательную часть задачи. Все это свидетельствует о необходимости при восприятии текста задачи использовать не только слуховые, но и зрительные, а если возможно, то и кинестезические анализаторы.
Задачу следует иллюстрировать. Для иллюстрации задач в 1—2-х классах учителя прибегают к предметной иллюстрации, используя с этой целью предметы окружающей действительности, ученические принадлежности, природный материал, игрушки, а затем и изображения этих предметов в виде трафаретов, которые демонстрируются с помощью наборных полотен, фланелеграфа, магнит-
13* 347

|
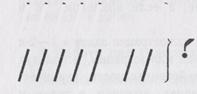
|
| ных досок, песочного ящика, ТОО и т. д. Широко используются для иллюстрации задачи плакаты, рисунки (рис. 30). |
Рис. 30
Если в 1-м классе текст задачи иллюстрируется с помощью предметов или рисунков, то в конце 1-го и во 2-м классе надо учить учащихся заменять элементы предметных множеств, о которых говорится в задаче, их символами, при этом сохраняя равночислен-ность множеств. Например, если в задаче речь идет о деревьях, то рисунок дерева заменяют палочки. Например, содержание задачи: «Дети посадили в одном ряду 5 дубков, а во втором — на 2 дубка больше. Сколько всего деревьев посадили дети?» — учащиеся могут зарисовать так, как показано на рисунке 31.
Символами тетрадей могут служить квадраты или прямоугольники, огурцов — овалы, яблок — круги и т. д.
Выполняя рисунок или иллюстрируя задачу предметами, учащиеся глубже проникают в предметно-действенную ситуацию задачи и легче устанавливают зависимость между данными, а также между данными и искомыми.
Естественно, что не каждую словесно сформулированную задачу нужно иллюстрировать или «опред
| Рис. 31 |
мечивать». Но, помня об особенностях мышления умственно отсталых школьников, к этому приему нужно время от времени прибегать, не только решая новые для учащихся задачи, но и повторяя решение уже
известных им видов задач. Причем использовать этот прием, как показывает опыт, следует не только в младших, но и в старших классах школы VIII вида, например при решении задач на краткое сравнение, приведение к единице, на нахождение части от числа и т. д. Постепенно учащиеся переходят от «опредмечивания» содержания задачи к «воображению» ими предметной ситуации. В этом случае учитель предлагает «вообразить» себе содержание задачи, представить, как это происходит в жизни с реальными объектами, описанными в задаче. Тем учащимся, которые еще не готовы к этому, можно разрешить продолжать использовать предметы, рисунок.
Наряду с конкретизацией содержания задачи с помощью предметов, трафаретов и рисунков в практике работы учителей школы VIII вида широкое распространение получили следующие формы записи содержания задачи:
1. Сокращенная форма записи, при которой из текста задачи
выписывают числовые данные и только те слова и выражения,
которые необходимы для понимания логического смысла задачи.
Вопрос задачи записывается полностью. Например: «В вазе стоял
букет цветов из ромашек и васильков. В букете было 7 ромашек,
а васильков на 5 штук больше. Сколько всего цветов в букете?»
Сокращенная запись: «Ромашек 7 штук, васильков на 5 штук
больше. Сколько всего цветов?»
2. Сокращенно-структурная форма записи, при которой каждая
логическая часть задачи записывается с новой строки. Вопрос
задачи записывается или внизу, или сбоку. Текст задачи принима
ет наглядно-воспринимаемую форму. Например:
| Сколько всего цветов? |
Ромашек7 штук. Васильков на 5 штук больше.
3. Схематическая форма записи. Это запись содержания задачи
в виде схемы (рис. 32). В схеме желательно сохранить пропорции,
соответствующие числовым данным. «В одном ящике 17 кг поми
доров, а в другом на 5 кг больше. Сколько килограммов помидо
ров в двух ящиках?»
4. Графическая форма записи. Это запись содержания задачи в
виде чертежа, диаграммы. Удобнее всего в графической форме
записывать задачи на движение (рис. 33).
5. Опыт показывает, что пониманию зависимости между число
выми данными, а также между данными и искомыми в некоторых
задачах способствует не конкретизация условия, а наоборот, аб-

|
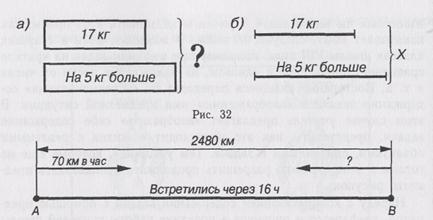
Рис. 33
»г
страгирование от конкретной ситуации. К таким задачам относятся задачи на пропорциональную зависимость (на соотношение скорости, времени и пути; цены, количества и стоимости и др.).
Для записи таких задач лучше всего использовать таблицу, в графы которой записываются числовые данные задачи. Например: «За 3 литра молока уплатили 7 р. 50 к. Сколько стоят 8 л молока?»
В данном случае абстрагирование от предметного содержания задачи помогает учащимся лучше осмыслить зависимость между данными и искомой величиной.
Указанным формам записи содержания задач умственно отсталых школьников необходимо учить так, чтобы они самостоятельно могли выбрать наиболее рациональную форму и записать задачу. Овладевают этими формами записи учащиеся медленно. Учителю необходимо соблюдать систему, поэтапность в обучении:
1. После ознакомления учащихся с текстом задачи учитель сам
дает краткую запись содержания задачи на доске, учащиеся запи
сывают ее одновременно с учителем в тетрадь.
2. После разбора условия задачи краткую запись на доске
делает ученик под руководством учителя, при активном участии
учащихся всего класса. С этой целью учитель просит ученика'
прочитать фрагмент задачи и спрашивает, как можно записать эту
часть задачи кратко, зарисовать или начертить.
3. Вызванный к доске ученик самостоятельно читает задачу и
дает ее краткую запись под контролем учителя. Учащиеся также
выполняют это задание самостоятельно и сверяют свою запись с
записью на доске.
4. Самостоятельная запись условия задачи учащимися.
Краткая форма записи задачи должна быть составлена так,
чтобы ученик мог по ней воспроизвести условие задачи или составить задачу.
Чтобы учащиеся научились записывать текст задачи кратко, нужно требовать от них по полному тексту задачи из учебника составить краткую запись задачи, не решая ее. Надо учить учащихся выбирать рациональную форму краткой записи, т. е. такую, в которой наиболее отчетливо вырисовывалась бы зависимость между данными задачи, а также между данными и искомым.
Содержание каждой ли арифметической задачи следует записывать учащимся? Безусловно, нет. Если предметная ситуация ясна, а с аналогичной математической зависимостью учащиеся неоднократно встречались и в своей практической деятельности, и при решении словесно сформулированных задач, то запись задачи в той или иной форме не нужна. Это сократит время на ее решение.
Следовательно, учить различным формам записи содержания задачи учащихся необходимо, использование же форм записи будет зависеть от имеющегося опыта учащихся, от степени трудности для них понимания предметной ситуации задачи и зависимости между данными и искомым.
Лучшему восприятию и пониманию задачи способствует ее повторение по вопросам.
Форма вопросов при повторении задач меняется: сначала учитель задает конкретные вопросы, а затем обобщенные. Например:
«В коробке было 3 красных карандаша. Вова положил туда еще 2 зеленых карандаша. Сколько всего карандашей в коробке?»
Повторение задачи по вопросам: «О чем эта задача? Какого цвета карандаши? Сколько красных карандашей лежало в коробке? Покажите цифрой. Сколько зеленых карандашей положили в коробку? Покажите цифрой. Что нужно узнать в задаче или какой вопрос задачи?»
Другая форма вопросов, с помощью которых выясняется значение каждого числового данного: «Что показывает число 3 в задаче? Что показывает число 2 в задаче? Какой вопрос задачи?»
Наконец, можно поставить к тексту задачи и такие вопросы: «Что известно в задаче? Что неизвестно в задаче? Что нужно узнать?» Для ответа на эти вопросы учащиеся после чтения задачи должны самостоятельно вычленить из текста задачи известные и неизвестные данные. Безусловно, это требует уже определенного опыта в анализе содержания задачи.
Не нашли, что искали? Воспользуйтесь поиском: