Умножение и деление десятичных дробей на целое число

Умножение и деление десятичных дробей на целое число тесно связано с умножением и делением целых чисел. Чтобы подвести учащихся к пониманию того, как производится умножение деся­тичной дроби на целое число, и сделать обобщение в виде прави­ла, необходимо начать с рассмотрения простейших случаев (при этом учитель должен воспользоваться тем, что учащиеся уже имеют понятие о действии умножения), например: 1,2-3=. В этом выражении действие умножения заменяется действием сло­жения: 1,2.3 = 1,2+1,2 + 1,2=3,6, 1,2-3=3,6. Внимание учащихся надо обратить на то, что сначала умножается целое число на множитель и это произведение целых отделяется запятой, а затем умножаются десятые доли на множитель. Подобные случаи умно­жения (без перехода через разряд ни в одном разряде) выполня­ются устно. Случаи умножения с переходом через разряд выпол-

Множители перемножаются как целые числа и в полученном произведении отделяется запятой справа столько цифр, сколько десятичных знаков в первом множителе.

Примеры на умножение десятичной дроби на целое число под­бираются в той же последовательности, что и примеры на умно­жение целых чисел.

Наибольшие трудности для учащихся представляют примеры, в которых в первом множителе один или несколько десятичных знаков равны нулю, а также примеры, в которых в произведении получается нуль целых.

Подобные примеры надо чаще предъявлять учащимся, повторив предварительно правила умножения нуля на целое число и целого

числа на нуль.

При делении десятичной дроби на целое число также следует соблюдать определенную последовательность:

1. Все разряды делимого делятся на делитель без остатка:
6,48:2=?. Делим на 2 сначала целые, отделяем целые в частном
запятой, потом делим десятые доли и, наконец, сотые доли:
6,48:2=3,24. Такие примеры решаются устно.

2. Целое или какая-либо из долей делимого не делится нацело

на делитель: 4,86:3.

Делим 4 целых на 3. В частном получаем едини­цу, отделяем ее запятой. В остатке осталась едини­ца. Дробим ее в десятые доли и прибавляем еще 8 десятых. 18 десятых делим на 3, получаем 6 деся­тых. Далее 6 сотых делим на 3, получаем 2 сотых. Частное равно 1,62.

3. Особые случаи деления, когда в частном получаются нули

Умножение и деление десятичных дробей, так же как и соот­ветствующие действия с целыми числами, изучаются параллельно. Каждое действие учащиеся учатся проверять обратным ему дейст­вием.

Решаются также примеры, в которых содержатся действия пер­вой и второй ступени со скобками, чтобы поупражнять учащихся в применении правил порядка действий. Кроме того, следует пред­ложить и примеры на нахождение неизвестного множимого, неиз­вестного делимого.

Запись десятичной дроби в виде обыкновенной и наоборот

С выражением десятичной дроби в виде обыкновенной учащие­ся уже сталкивались неоднократно. Во-первых, образование деся­тичной дроби рассматривалось как частный случай обыкновенной дроби, у которой знаменатель — единица с нулями, во-вторых, десятичную дробь в виде обыкновенной учащиеся выражали при знакомстве с действиями над десятичными дробями. Запись деся­тичной дроби в виде обыкновенной сводится к записи десятичной дроби со знаменателем,например: 0,3=3/10

Обратное упражнение, т. е. запись обыкновенной дроби в виде десятичной, выполняется так:

У обыкновенной дроби знаменатель дроби 5, у десятичной

же дроби знаменатель должен выражаться единицей с нулями, т. е. 10, 100, 1000 и т. д. Подбираем такое число, при умножении на которое числа 5 получалось бы 10, 100, 1000, т. е. знаменатель дроби выразился бы единицей с нулями. Если 5-2, то получится 10. Чтобы дробь не изменилась, надо и числитель умножить на 2.

Следовательно, Запишем дробь 3/4в виде деся-

тичной. Для этого нужно, чтобы знаменатель этой дроби стал равен 10, 100 или 1000. В десятых долях эту дробь выразить нельзя, так как 10 не делится на 4 нацело. Посмотрим, нельзя ли вы­разить эту дробь в сотых долях:100:4=25.Значит, и числитель,и знаменатель дроби ¾ надо умножить на 25 (дополнительный множитель 25). Следовательно, Выразим

дробь в десятичных долях. Знаменатель 10 не подходит, так как

10 не 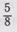делится на 8 нацело, знаменатель 100 тоже не подходит по той же причине, попробуем взять знаменатель 1000:8=125 (до­полнительный множитель 125). Следовательно.

Но не всегда этим способом можно (при замене обыкновенной дроби десятичной) выразить знаменатель обыкновенной дроби 1 с

несколькими нулями. Возьмем, например, дробь -д-. Попробуем

взять знаменатель 10. Он не подходит, так как нельзя в данном случае получить дополнительный множитель: 10 не делится наце­ло на 3. То же получим, если возьмем знаменатели 100, 1000. Следовательно, дробь -о- нельзя этим способом выразить десятич­ной дробью.

Существует второй способ замены обыкновенной дроби деся­тичной. Всякую обыкновенную дробь можно рассматривать как

3 частное от деления числителя на ее знаменатель. Возьмем дробь -г.

Ее можно рассматривать как частное от деления 3 на 4. Выпол­ним деление:

Рассуждение: «3 на 4 не делится нацело. В част­ном пишем нуль целых и ставим после нуля запя­тую. Раздробляем 3 в десятые доли. 30 десятых делим на 4. В частном пишем 7 десятых. В остатке 2 десятых. Раздробим 2 десятых в сотые доли. Полу­чим 20 сотых. Делим на 4. В частном 5 сотых.

Итого в частном 0,75. Следовательно,

Проверка. Нужно частное умножить на делитель. В произве­дении должно получиться число, равное делимому:

После рассмотрения еще нескольких примеров учащиеся долж­ны сами сделать вывод о том, как обыкновенную дробь заменить десятичной.

«Вернемся к дроби 1/3. Мы видели, что

Дробь 1/3, нельзя заменить десятичной первым

способом. Попробуем заменить ее десятичной вторым способом, т. е. делением числителя на знаменатель. Если будем продолжать делить дальше, то увидим, что всегда в остатке будет единица, а в частном 3. Деление можно про­должить бесконечно. Но обычно его прерыва­ют, делят до первого, второго или третьего знака после запятой, например: 1:3=0,333...». В данном случае деление закончили на тысячных долях. Точки показывают, что деление можно продолжить и дальше. 0,333... —

приближенное, неточное значение дроби 1/3. Можно предложить учащимся обратить в десятичные еще ряд обыкновенных дробей:

Получаются приближенные десятичные дроби.

После рассмотрения замены различных обыкновенных дробей десятичными учащиеся убеждаются, что одни обыкновенные дроби можно точно выразить десятичными — в этом случае полу­чаются конечные десятичные дроби 1/5 = 0,2 ], другие же можно заменить только бесконечными десятичными дробями

1/3= 0,333...!.»

Не нашли, что искали? Воспользуйтесь поиском: