МЕТОДИКА ИЗУЧЕНИЯ ДЕСЯТИЧНЫХ ДРОБЕЙ И ПРОЦЕНТОВ

С десятичными дробями учащиеся школы VIII вида знакомятся после изучения целых чисел и обыкновенных дробей.

Изучение десятичных дробей позволяет закрепить знания уча­щихся о целых числах, лучше осознать принцип десятичной сис­темы счисления, поместное значение цифр в числе, закрепить навыки выполнения арифметических действий, глубже осознать свойства, преобразования и действия с дробями вообще. Кроме того, это дает возможность обобщить знания учащихся о всех изученных числах.

Десятичные дроби чаще, чем обыкновенные, используются в жизни и имеют большое практическое применение. С десятичны­ми дробями учащиеся будут встречаться и в учебных мастерских, и на производстве, и в быту.

Последовательность изучения десятичных дробей такова: полу­чение и запись десятичных дробей, преобразование, сравнение, арифметические действия, запись чисел, полученных при измере­нии величин, в виде десятичной дроби и наоборот.

При изучении этой темы необходимо широко использовать на­глядные пособия: квадрат, разделенный на 10 горизонтальных

полос и на 100 равных клеток (каждая из полос обозначает 0,1, а каждая из клеток — 0,01 часть квадрата); отрезки, разделенные на 10 равных частей: метры, разделенные на дециметры, санти­метры и миллиметры; таблица классов разрядов и десятичных долей.

ПОЛУЧЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ

Успех усвоения десятичных дробей во многом зависит от зна­ния учащимися нумерации целых чисел, свойств десятичной сис­темы счисления и десятичного соотношения мер метрической сис­темы (длины, стоимости, массы). Все эти знания необходимо вос­произвести в памяти учащихся перед тем, как переходить к изуче­нию десятичных дробей.

Учитывая конкретность мышления умственно отсталых уча­щихся, понятие о десятичной дроби целесообразнее всего сформи­ровать, используя знания учащихся о соотношениях метрической системы единиц измерения длины. В качестве наглядного пособия используется метр, разделенный на дециметры, сантиметры и мил­лиметры. Учащиеся вспоминают, что в 1 м содержится 10 дм, 100 см и 1000 мм. Теперь можно установить, какую часть метра составляет 1 дм,1 см, 1 мм, и записать: 1 дм= 1/10 м, 1 см=1/100м, 1 мм=1/1000м, 1 м= 1 /1000км.

Таким образом повторяется соотношение единиц измерения стоимости и устанавливается, что 1 к.=1/100 р. После повторения соотношения

единиц измерения массы учитель на доске, а уча­щиеся в тетрадях записывают, что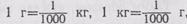

Учитель просит учащихся записать подряд без наименования все дроби, которые получили, с тем чтобы обратить внимание на знаменатели этих дробей. Учащиеся на основе наблюдений уста­навливают, что у всех дробей знаменатели 10, 100, 1000, т. е. единица с одним или несколькими нулями. Учитель формулирует вывод: дробь, у которой знаменатель — единица с одним или несколькими нулями, называется десятичной дробью.

Далее учащимся предлагается записать под диктовку несколько дробей и объяснить, как

получилась каждая из дробей, а затем назвать и написать только десятичные дроби. При этом следует подчеркнуть общность в полу­чении обыкновенных и десятичных дробей: при получении десятич­ных дробей целое (единица) делится на 10, 100, 1000 и т. д. равных частей, т. е. на столько равных частей, сколько единиц в знаменателе. Например, чтобы получить дробь -^г, надо взять

отрезок (единицу) и разделить его на 10 равных частей, а затем взять 7 таких частей (рис. 27).

Десятичная дробь может получаться и при измерении. Напри­мер, при измерении ленты длина ее оказалась оавной 8 дм, или 80 см, а это составляет м, или— десятичные

дроби.

Письменная нумерация десятичных дробей тесно связана с нуме­рацией целых чисел, со свойствами десятичной системы счисления. Поэтому, прежде чем дать запись десятичных дробей, следует вспом­нить нумерацию целых чисел, повторить поместное значение цифры в числе. Например, в числе 111 цифра 1, стоящая на первом месте справа, означает 1 единицу; цифра 1, стоящая на втором месте спра­ва, означает 1 десяток; цифра 1, стоящая на третьем месте справа, означает 1 сотню.

Таким образом, каждая цифра, стоящая левее данной, обозна­чает единицы, которые в 10 раз больше данной.

Таким образом, выделяется главное свойство соседних разря­дов: единицы разряда справа в 10 раз меньше единиц разряда, находящегося от него слева. Если, например, разрядную единицу переместить слева направо, то она уменьшится в 10 раз. Справа от разряда единиц, за границей целых чисел, находится разряд, в 10 раз меньший, т. е. десятые доли, далее сотые, тысячные и т. д. Таким образом, место десятичных долей в таблице классов и разрядов определено.

Если рассматривать цифры в числе 111 слева направо, то каждая цифра, стоящая справа от данной, обозначает единицы, 320

которые в 10 раз меньше данной. Запишем число 111 и обозначим разряды в этом числе.

Если справа от числа 111 напи­сать цифру 1, то она будет обозначать число, в 10 раз меньшее, чем 1 единица. Это одна десятая доля единицы.

Если справа записать еще 1 единицу, то она будет меньше десятой доли в 10 раз и единицы в 100 раз. Это'одна сотая доля единицы.

В таблице целые числа от десятичных долей отделяются чер­той. На письме целая часть от дробной части отделяется запятой: 111, 1. Читается эта десятичная дробь так: сто одиннадцать целых одна десятая.

Если в дроби нет ни одной целой, то вместо нее пишется нуль.

Например, обыкновенную дробь можно записать без знаменате­ля так: 0,1. Читается эта дробь так: нуль целых одна десятая. Следует сравнить и запись обыкновенных и десятичных дробей:

Объяснить запись десятичной дроби можно, используя числа, полученные от измерения. Сначала взять числа с соотношением между крупными и мелкими мерами, равными 10, затем 100, наконец 1000.

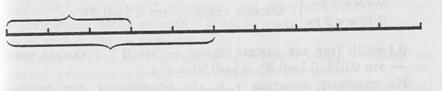
Например, 1 см 5 мм можно записать с одним наименованием, рассуждая следующим образом: в числе 1 см 5 мм есть 1 целый сантиметр и 5 мм, которые составляют 5 десятых сантиметра, т. к. 1 мм равен одной десятой сантиметра. Это число можно записать десятичной дробью: 1, 5 см, т. е. написать целое число сантиметров (1) поставить запятую, а 5 десятых сантиметра, т. е. десятые доли сантиметра пишутся после целых (после запятой).

11 Перова М. Н.

Знаменатель 10 не пишется, но читается: одна целая пять десятых сантиметра. После записи чисел с соотношением между мерами измерения, равным 10, аналогично объяснить запись чисел полу­ченных от измерения с соотношением мер, равным 100 (затем 1000) и запись этих чисел десятичной дробью.

Например, 3 р. 25 к.=3,25 р. (в одном рубле 100 копеек, значит 25 к. — это 25 сотых частей рубля: записывается целое число 3, ставится запятая, а после нее пишется 25 сотых, т. е. 3,25 р., знаменатель не пишется, но читается. 10 р. 08 к. = 10,08 р., 1 ц 05 кг=1,05 ц и т. д.

Аналогично записываются десятичной дробью именованные числа с соотношением мер, равным 1000. Например, 1 кг 375 г= 1,375 кг, 5 кг 085 г=5,085 кг, 7 т 004 кг=7,004 т.

При записи десятичных дробей используют разрядную сетку, в которой указаны десятичные доли.

Разрядная сетка помогает правильно записывать десятичные дроби, например: 17,8; 4,76; 375,6; 18 875 и т. д.

Наибольшую трудность для учащихся представляет запись де­сятичных дробей (так же как и целых чисел) с отсутствующими разрядными долями, например: 19,07; 25,905; 27,009. Поэтому эти дроби даются для записи только тогда, когда учащиеся хорошо усвоят запись дробей с наличием всех разрядных долей, могут объяснить, как называется каждая разрядная доля, на каком месте справа от запятой она стоит, поймут, что каждая последую­щая доля в 10 раз меньше предыдущей (если имеет одно и то же число долей). Например, 5 сотых в 10 раз меньше, чем 5 десятых, а 5 тысячных в 10 раз меньше, чем 5 сотых.

При знакомстве с письменной нумерацией десятичных дробей необходимо обратить внимание учащихся на то, что после запятой в десятичной дроби должно стоять столько знаков, сколько нулей в знаменателе дроби. Например, надо записать дробь семь целых восемь сотых. Знаменатель дроби 100, т. е. имеет два нуля. Сле­довательно, после запятой должно быть два знака, произносится же только один знак (число 8), значит, сразу после запятой надо написать нуль: 7,08. На особенность, которую мы используем при записи десятичных дробей, следует обратить внимание учащихся и при их чтении.

При чтении десятичных дробей учащиеся школы VIII вида за­трудняются в назывании знаменателя десятичной дроби. Они либо его не называют (например, дробь 0,375 читают так: нуль целых триста семьдесят пять), либо вместо тысячных говорят десятые, сотые (нуль целых триста семьдесят пять сотых, десятых).

Чтобы снять эту трудность при чтении десятичных дробей, следует показать учащимся, что если после запятой стоит один знак (цифра), то знаменатель этой дроби — единица с одним нулем, т. е. десять, и нужно добавлять слово «десятых» (соответ­ственно указать на дроби с сотыми и тысячными долями).

Не нашли, что искали? Воспользуйтесь поиском: